CBSE Physics Experiment Measurement of Length

Length is a physical quantity. Measurement of length is the process of determining an object's length in a set of predetermined units, which may be standard or not. For example, a metre can be used to estimate the length of a pencil in inches. A foot scale can be used to gauge the height of each student in a class. There are different measuring instruments which measure the length with different accuracy.  In this article, let's study more in-depth how length is measured.

Table of Contents 

• Aim

• Meter Scale

• Vernier Callipers

• The principle of Micro Meter Screw

• Screw Gauge

• Spherometer

• Lab Manual Questions

• Viva Questions

• Practical based Questions

• Conclusion

Aim

Measurement of Length

Meter Scale

Theory

The simplest tool used in laboratories to measure small lengths is a wooden or steel scale. It has two sides, one is centimetre/millimetre and the other in inches. The length can only be accurately measured up to 1 mm because the smallest division on the metre scale is 1 mm. The following table shows the relation of other units with base units: 

• 1 kilometre (km) = 1000 metres (m)

• 1 hectometer (hm) = 100 m

• 1 decameter (dam) = 10 m

• 1 decimeter (dm) = 1/10 m = 0.1 m

• 1 centimetre (cm) = 1/100 m = 0.01 m

• 1 millimetre (mm) = 1/1000 m = 0.001 m

Procedure

1. Depending on which unit you want to measure length choose the side of the scale. Take the ruler's centimetres side if you want a measurement in centimetres. Take the ruler's inches side if you want the measurement to be in inches.

2. Place the item next to the ruler, beginning at point 0.

3. Mark the value at the endpoint. 

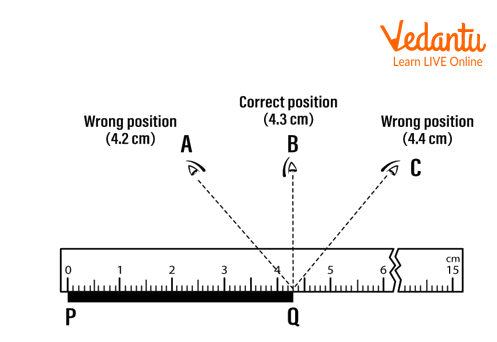
Correct Way to Measure Using Metre Scale

Precautions

1. Maintaining the scale's edge along the object's length is necessary. If the scale is kept inclined it adds length. 

2. The object whose length is to be measured should have one of its edges lined up with a predetermined mark on the scale.

3. Use of the scale's zero mark should be avoided because it usually has a worn-out edge.

4. The reading should be obtained with one eye closed and the other eye directly over the mark. A tilted eye will read incorrectly due to parallax error.

5. Without touching the object or the metre scale, look at the other edge of the object, where the scale reading is taken. The length of the object is determined by the difference between the scale readings of the two edges.

Vernier Callipers

Vernier Callipers

The different parts of the Vernier Callipers are

1. Main scale:  It consists of a steel metallic strip M that is graduated in inches and tenths of an inch on one face and centimetres and millimetres on the other.

2. Vernier Scale:  The strip M moves over a vernier scale V. By using screw S, it may be fixed in any position. Both sides have graded edges. The vernier scale's side that slides over the mm side have ten divisions over a length of nine millimetres, or over nine main scale divisions, and the vernier scale's side that slides over the inches side have ten divisions over a length of nine mill inches, or over nine major scale divisions.

3. Adjustable jaws:  Jaws on the vernier scale are protruding at a right angle to the main scale. They are referred to as moveable jaws. 

The main scale reading (M.S.R.) equals N if, with the body between the jaws, the vernier scale's zero is placed before the main scale's Nth division. Vernier scale reading (V.S.R.) = n x if any division of the main scale coincides with the nth division of the vernier scale (L.C.) (L.C. is the vernier callipers' least count)

= n x (V.C.) (V.C. is vernier constant of vernier callipers) (V.C. is vernier constant of vernier callipers)
Total reading T.R. = M.S.R. + V.S.R. (LC equals V.C.).

Procedure

To Determine Zero Error, Zero Correction

1. Find the vernier constant (V.C. ), also known as the least count (L.C.) of the vernier callipers, and write it down step by step.

2. Bring the movable jaw BD and the fixed jaw AC into proximity to determine zero inaccuracy. Then, write them down three times. If there is no zero error, write "zero error nil."

3. When the jaws are open, insert the object between jaws A and B, then adjust jaw DB so that it gently grasps the body without applying excessive pressure. Tighten the screw S holding the vernier scale V in place.

4. Keep in mind where the vernier scale's zero mark is located on the main scale. Before the vernier scale's zero point, note the main scale reading.

5. Make a table of your observations.

6. Apply the zero correction to your calculations for each dimension.

7. Calculate the mean using various values for the same dimension.

Precautions

1. Vernier scale motion on the main scale should be smooth (by oil if necessary).

2. It is important to carefully seek out and accurately record the vernier constant and zero error.

3. Gripping the body between the jaws should be forceful but gentle (without undue pressure on it from the jaws).

4. Observations should be made from at least three separate locations, all of which should be approached from a right angle.

The Principle of Micro Meter Screw

Vernier callipers, which are typically seen in laboratories, allow us to measure length accurately to 0.01 cm. Screw gauge and spherometers, which are based on the micrometre screw principle, are used when lengths need to be measured more precisely, like up to 0.001 cm. When the screw is given a full spin, the linear distance it moves is equal to the distance between two adjacent threads, measured along the screw's axis. This distance between threads is called the pitch of the screw. The most common values are 1 or 0.5 millimetres. On one end of the screw, a circular cap or disc is fastened, and its circumference is often divided into 100 or 50 equal portions. If the circle scale is divided into 100 equal parts and rotated through one circular scale division, the screw will travel forward or backwards by 1/100 of the pitch. The least count of the screw is the shortest distance that can be precisely measured.

The screw gauge and the spherometer consist of the following two scales: 

(i) Pitch or linear scale. It is a scale that is perpendicular to the screw's axis. 

(ii) Head or circular scale. It is inscribed around the circumference of the spherical disc or the screw cap.

Screw Gauge

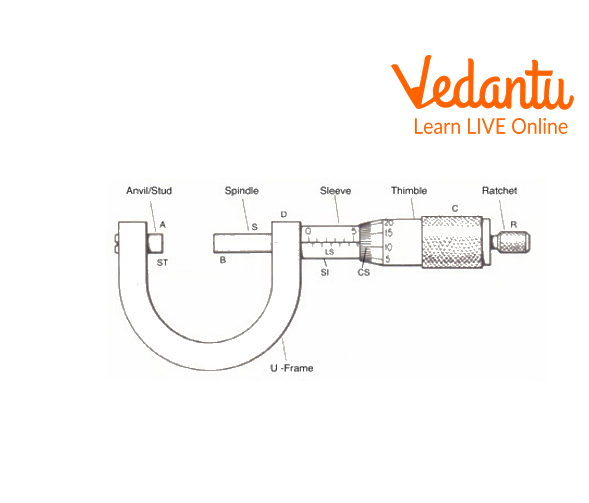
Schematic of the Screw Gauge and its Components. 

The operation of a screw gauge is based on a micrometre screw. It is made out of a metal frame in the shape of a U. A small, substantial component made of gun metal is fastened to one end of the frame. It has a planar face and is referred to as a stud.

M has another end D that is attached to a cylindrical hub SI. A millimetre or so of the hub elongates from the frame's end. A reference line is drawn on the cylindrical hub parallel to its axis. Depending on the screw pitch, graduations on the reference line are in millimetres and half-millimetres. This scale is also known as the pitch scale or linear scale. The hub and frame D are connected using a nut. A gunmetal screw S travels through the nut. The screw's front face B, which faces the plane face A, is also flat. When the screw is turned, a hollow cylindrical cap, designated thimble, can revolve over the hub. It is fastened to the screw's right-hand end. The screw either moves in or out as the cap is rotated. The circular surface CS is separated into 50 or 100 equally sized segments. Ritchet (R) refers to the right-hand end of the thimble that has been milled for a secure grasp. 

Zero Error and Zero Correction

When faces A and B are just touching each other, the zero mark of the circular scale may not line up with the zero of the pitch scale in some instruments owing to wear and tear or a manufacturing error.

Such instruments are error- and correction-free. The zero error is negative and the zero correction is positive if the circular scale's zero moves past the reference line. The zero error and zero correction are positive and negative, respectively, if it is placed behind the reference line.

Back-Lash Error

There is some gap left for the screw and nut to move around because of wear and tear or lose fitting. In such instruments, moving the screw in one direction and then rotating it backwards may prevent the screw from moving along the axis for a noticeable rotation of the head. The screw must always be rotated in the same direction for a specific set of observations to reduce this mistake.

Determination of Pitch, Least Count and Zero Error of Screw Gauge

1. Determining the pitch and the least count: Pitch, which is equal to the distance between two consecutive threads, is the linear distance covered by a screw during a full spin. Take note of the divisions of the linear scale (pitch). Screw rotation will align the reference line with the zero mark on the circular (head) scale. Take note of how many linear scale divisions the cap leaves uncovered.

Give the screw a known number of revolutions at this point. (One rotation is finished when the circular scale's zero once more touches the reference line.) Recall the reading from the linear scale. To determine the distance the screw moved, find the difference between two readings on a linear scale.

2. Determination of zero error and zero correction: To do this, the screw is turned forward until the edge of the cap meets the zero mark of the linear scale and plane face B of the screw just barely touches the fixed plane face A of the stud. The screw gauge is maintained while the linear scale's zero is positioned downward and vertically.

One of the following three situations will arise :

(i) Zero mark of circular scale comes on the reference line.

In this case, zero error and zero correction, both are nil.

Actual thickness = Observed (measured) thickness.

(ii) Zero mark of the circular scale remains on the right of the reference line and does not cross it. In this case, the 2nd division on the circular scale comes on the reference line. Zero reading is already 0.02 mm. It makes zero error + 0.02 mm and zero correction – 0.02 mm. The measured thickness will be 0.02 mm less than the actual thickness.

(iii) Zero mark of the circular scale goes to the left of the reference line after crossing it. Here zero of the circular scale has advanced from the reference line by 3 divisions on a circular scale. A backward rotation by 0.03 mm will make the reading zero. It makes zero error -0.03 mm and zero correction + 0.03 mm. Therefore, the actual thickness will be 0.03 mm more than the observed (measured) thickness.

Spherometer

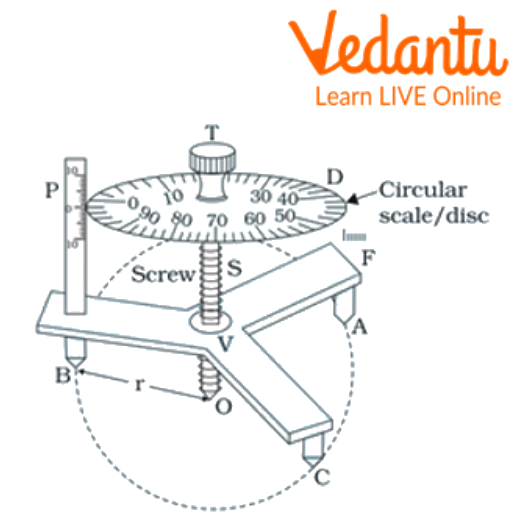
Schematic of the Spherometer with its Components

It functions using the micrometre screw principle. A spherometer is the name of a device that is used to measure the radius of curvature of a spherical surface or very thin thickness. 

It comprises a metallic tripod structure with three equal-length fixed legs. The three legs' tips always lay in the same plane at the corners of an equilateral triangle.

A vertical nut is attached in the middle of the tripod frame. This nut is capable of accommodating a precisely cut screw. The screw's axis runs parallel to each of the three legs. At the top of the screw is a sizable round disc D that ends in a machined head. A circular disc's circumference is divided into 100 or 200 equally-sized pieces. At one end of the tripod, the frame is a small vertical scale, P, that is often divided into millimetres or half millimetres. The scale P barely brushes the rim of the circular disc and runs parallel to the screw's axis. P is another name for the pitch scale.

Determination of Least Count: 

1. Find the value of the first division on the pitch scale before measuring the screw's pitch. Next, align the zero of the circular scale opposite the pitch scale, and turn the screw n times (4 or 5).

2. On the pitch scale, take note of the distance d the screw moved. The formula for the screw's pitch, p, is given by: p=d/n mm = 1 mm.

3. The lowest count of the screw is equal to P/N mm or 0.001 cm if the circular scale on the disc's circumference has N divisions.

4. Place the spherometer on a large glass slab such that its three legs rest on it to measure the thickness of a glass strip. Raise the screw high enough to allow for a thin glass strip placement below the screw, the thickness of which needs to be specified. Gently turn the screw lower until the tip of the screw just touches the glass strip.

5. To test this, gently press at one of the spherometer's outside legs and attempt to insert a thin piece of paper beneath the other two legs or the centre screw. The screw only touches the upper surface of the glass strip if it cannot be introduced at any position.

6. Take note of the circular scale's reading, which corresponds to the pitch scale. Turn the screw down until the point of the screw just reaches the plane surface of the glass slab, then remove the glass strip from beneath the screw. Count the number of full rotations the disc made, using the initial reading of the circular scale as a point of reference, and then note how many additional circular scale divisions there are then there were full rotations.

7. The method described below can also be used to determine the value of x:

• If the circular scale's initial and final readings are a and b, respectively, then:

• (1) If zero of the circular scale does not move across the vertical scale P, then x for circular scales with clockwise graduation is equal to (a - b) and for circular scales with anticlockwise progression is equal to (b - a).

• (2) If zero of the circular scale moves across the vertical scale P, then x is equal to [(100 -a)-b] for clockwise graduation and [(100 — b)—a] for anticlockwise graduation.

Lab Manual Questions

1. How will increasing more divisions to a vernier scale on a vernier calliper affect the precision of the measurement?

Ans. Increases in vernier divisions don't do anything. In actuality, it will reduce the instrument's accuracy.

2. What makes a screw gauge a micrometre?

Ans. Since a screw gauge can measure lengths on the order of one micrometre, it's occasionally known as a micrometre.

3. The pitch is measured in which two units?

Ans. The pitch is measured using the circle and pitch scales, respectively.

4. What are the screw gauge's two fundamental components?

Ans. The main components of the screw gauge are the nut and the bolt.

Viva Questions

1. What are the direct methods of measuring length?

Ans. The direct methods of measuring length are measuring instruments such as Vernier callipers, micrometres, and coordinate measuring machines. These instruments are used to measure the dimensions of the target directly, also known as absolute measurements.

2. How do we use length in everyday life?

Ans. One of the most often used measurements daily is length. This may tell you your height, the width of a refrigerator, or how distant the closest town is. It can be used in science to measure things on various scales, from the diameter of an atom to the size of the universe.

3. Why does the vernier scale differ from the main scale?

Ans. The Vernier calliper's main (stationary) scale is divided into millimetres. The Vernier (moveable) scale has 10 divisions and is 9 mm long. Therefore, the Vernier scale's divisions are each 0.9 mm long, 0.1 mm shorter than the divisions of the main scale.

4. What does "zero error" mean?

Ans. Zero error of measuring device is considered zero inaccuracy when it doesn't need to take a reading. When this occurs with Vernier callipers, it is known as a zero error since the main scale's zero does not match the vernier scale zero.

5. What does "pitch of a screw" mean?

Ans. Pitch is the separation along the axis of the screw between the two closest (consecutive or successive) threads.

6. How is the L.C. of a screw gauge found?

Ans. Using the relation, we can find the least count of Screw Gauges.

 L.C. = Pitch of the screw/ No. of circular scale divisions.

7. Why is the instrument given the name “spherometer”?

Ans. The spherometer is named a spherometer because it is used to determine the radius of curvature of a spherical surface.

8. How can the least count of the spherometer be determined?

Ans. 

L.C. of spherometer = Pitch of screw/ no. of circular divisions

9. When is Z.E. positive and when is Z.E. negative in the screw gauge?

Ans. The zero error is positive if the edge of the circular disc is at the main scale's zero and the circular scale's zero is in front of the main scale's edge. The Z.E. is negative if it is behind the main scale's edge.

10. Name the physical quantity which is measured using a metre scale.

Ans. The physical quantity which is measured using a metre scale is length.

Practical Based Questions

1. To reduce the least count error, instruments need higher

1. Accuracy

2. Resolution

Ans. (b) To reduce the least count error, instruments need higher Resolution.

2. Who invented vernier callipers?

1. Pierre Vernier

2. William Gascoigne

3. Johann Schweigger

Ans. (a) Pierre Vernier invented vernier callipers.

     3. If the reading is 0.05 mm, what would be the positive zero error?

1. 0 

2. 0.1 mm 

3. +0.05 mm 

4. -0.05 mm

Ans. (c) If the reading is 0.05 mm then the positive zero error is +0.05 mm.

4. Which of the following devices cannot measure distance? 

1. Vernier Calliper

2. Micrometre

3. Ruler

4. Protractor

Ans. (d) The protractor cannot measure the distance. Vernier Callipers and Micrometres are used to measure distances accurately. The ruler's accuracy rating is one-tenth of a millimetre.

5. How are systematic errors removed usually for an instrument?

1. By replacing it

2. By re-calibrating it

3. By using a repair service

4. By not using it for some time

Ans. (b) Carelessness or excessive usage of an instrument can lead to systematic mistakes. By recalibrating the instrument and keeping it in good working order, it is simple to remove.

6. How many divisions are there in the vernier scale?

1. 2

2. 5

3. 10

4. 20

Ans. (c) The main (fixed) scale on the Vernier calliper is divided into millimetres. The Vernier (moveable) scale has 10 divisions and is 9 mm long.

7. What is the least count of the spherometer?

1. 0.1 mm

2. 0.1 cm

3. 0.01 mm

4. 0.01 cm

Ans. (c) The least count of the spherometer is 0.01 mm.

8. What is the least count of the metre scale?

1. 0.1 mm

2. 0.1 cm

3. 1 mm

4. 0.01 cm

Ans. (c) The least count of the metre scale is 1 mm. 

9. What is the least count of screw gauges?

1. 0.1 mm

2. 0.1 cm

3. 0.01 mm

4. 0.01 cm

Ans. (c) The least count of the micro-meter is 0.01mm. 

10. Who invented the Screw Gauge?

1. Pierre Vernier

2. William Gascoigne

3. Johann Schweigger

Ans. (b) William Gascoigne invented Screw Gauge.

Conclusion

From the above experiment, we learn how to measure the length of a body using various measuring instruments. The physical quantity length can be measured using a metre scale, vernier calliper, screw gauge, and a spherometer. Further, we have discussed how we can measure length using a metre scale, vernier callipers and what things we should keep in mind to get 100 per accuracy. We have also learnt about the construction of these measuring instruments, what parts they have, what is Pitch scale, what is Ritchet and much more. Also, we can reduce the chance of errors by recalibrating the instrument and keeping it in good working order. In the end, we have learnt how these measuring instruments differ from each other to measure with different accuracy.