Motion of a Body Down an Inclined Plane

The normal force behaves differently on an inclined plane than it does normally. Normal force has always been perceived to be upward and clockwise in relation to the direction of gravity up to this point. Technically, normal forces are never upward, but are always perpendicular to the surface an object is on. Calculating the net force acting on an object on an inclined plane is difficult because the two forces acting on the body are not moving in opposite directions. If one of the forces acting on the object can be divided into perpendicular components, adding additional forces will be simpler.

When we move the heavier objects we take help of the inclined plane to reduce the efforts just like loading and unloading the heavy appliances or objects from a building or in a mini truck/van. It is believed that in the construction of famous Egyptian pyramids the inclined planes were effectively used to move the heavier stone blocks.

Aim

• To evaluate the downward force along an inclined plane acting on a roller as a result of the earth's gravity.

• To understand the relationship with the angle of inclination θ by plotting a graph between the applied force and sin θ.

Theory

Take a look at the configuration in image A. A roller with mass M1 has been positioned in this instance on an inclined plane at an angle θ of with the horizontal. By changing the weights on the pan suspended with a string and connecting its other end to the mass through a pulley mounted at the inclined plane's top, an upward force along the inclined plane could be delivered to the mass M1. When mass M1 is travelling with constant speed v, the force acting on it is 

\[W = {M_1}g\sin \theta  - {f_r}\]

where W is the overall tension in the string \[W = weight~suspended\], M1 is the mass of the roller, and fr is the rolling-induced friction force. assuming that there is no resistance between the string and the pulley.

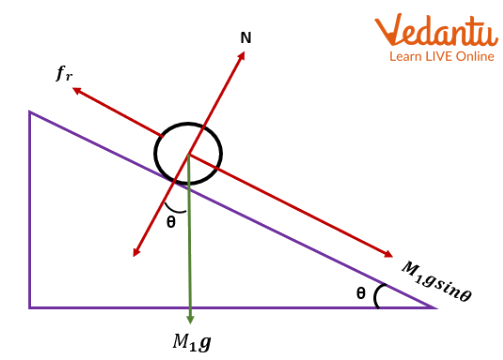
Free Body Diagram of an Object on an Inclined Plane.

The above image suggests that the perpendicular component of gravity, which is pointing in the opposite direction, balances the normal force. The parallel component of gravity is what causes this acceleration. A parallel component of gravity is the net force.

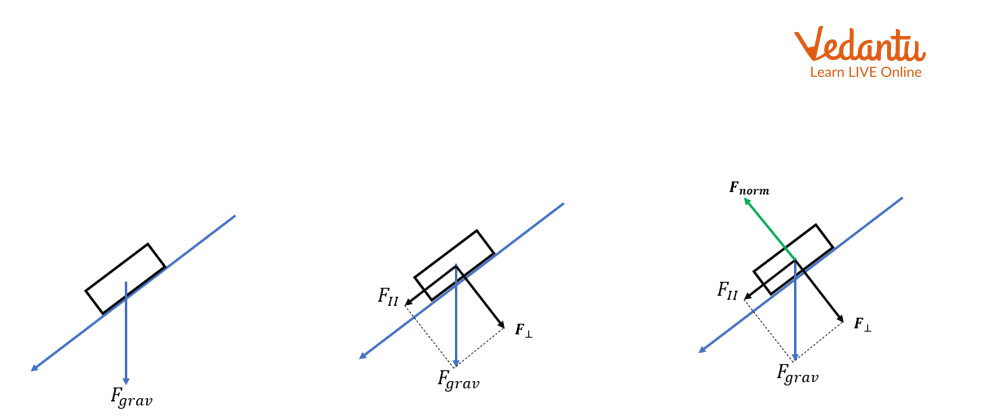
Force Free Body Diagrams.

Here,

\[{F_ \bot } = {F_{norm}}\]

And FII is the net force

so,

\[{F_\parallel } = mg\sin \theta \]

\[{F_ \bot } = mg\cos \theta \]

Apparatus required

• Pulley

• Roller

• Weight box

• Incline plane with protector

• Spirit level

• Spring balance

• Pan and thread

Procedure

• As indicated in image B, place the inclined plane, roller, and masses in the pan. Make sure there is no friction on the pulley. If necessary, lubricate it with machine oil.

• To begin, let's adjust W's value such that it may be used to calculate the roller to maintain its resting position on the incline plane.

• Start gradually reducing the masses in the pan until the roller just begins to descend the plane with a constant velocity. Take note of W and the angle θ. The free body diagram for the scenario in which the roller is just starting to descend is shown in Image A.

• Steps 2 and 3 should be repeated for various values of. Make a list of your findings.

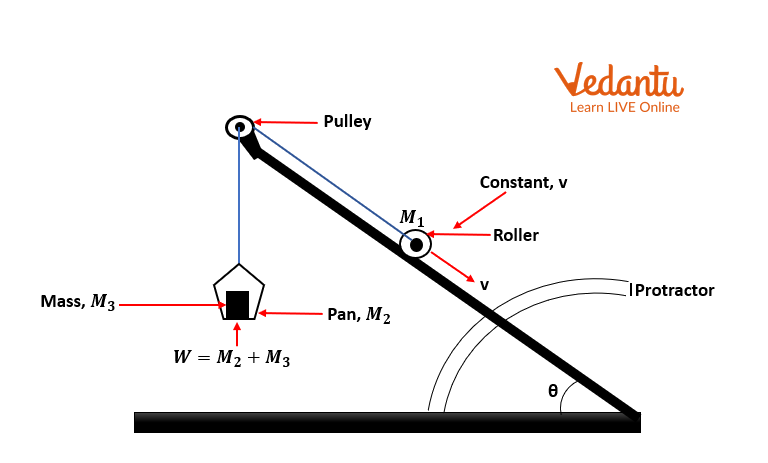
An Experimental Setup to Determine the Downward Force Along an Inclined Plane

Observations

• Gravitational acceleration, g = _____m/s2

• Mass of the Roller, m = ____$M_1$g

• Mass of the pan = _____$M_2$g

Graph

Plotting the relationship between sin and force W. It ought to be a straight line.

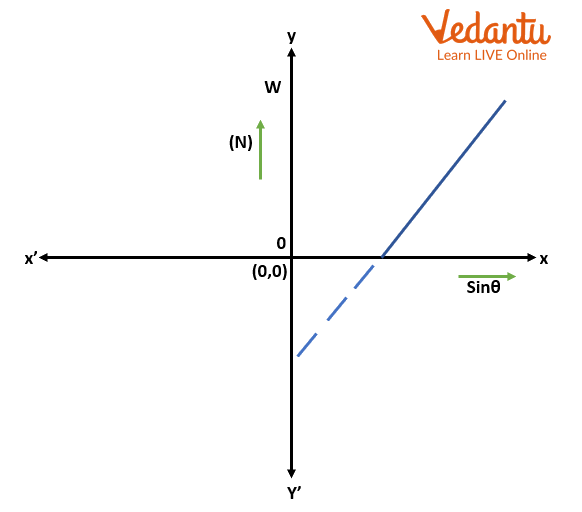
Graph Showing the Relationship between W and Sin Θ

Result

Consequently, within experimental error, downward force along inclined plane has a direct relationship to sinθ, where sinθ is the angle of inclination of the plane.

Precautions

• Using the spirit level, make sure the inclined plane is positioned on a horizontal surface.

• A frictionless pulley is required.

• The weight shouldn't touch the table or any other objects and should hang freely.

• The roller should move without slipping or smoothly.

• We should be reduced gradually as weight.

Lab Manual Questions

1. Give an example of a situation where the direction of motion and the force of friction are the same.

Ans: The car accelerates forward as you pull away from a stoplight due to ground friction on the tyres. As you move forward from a stop, the floor's friction with your shoes produces your acceleration.

2. What correlation existed between the plane's angle of inclination and the downward force due to the object's weight?

Ans: \[w - mg\sin \theta \] , describes the relationship between the downward force and angle of inclination.

3. How will you ensure that the roller travels up and down with continuous speed?

Ans: It must not be being affected by any outside forces. There won't be any acceleration if there is no force at work.

4. Why are we using an inclined plane for this experiment?

Ans: To evaluate the downward force along an inclined plane acting on a roller as a result of the earth's gravity and a load can be raised or lowered with the help of an inclined plane.

Viva Questions

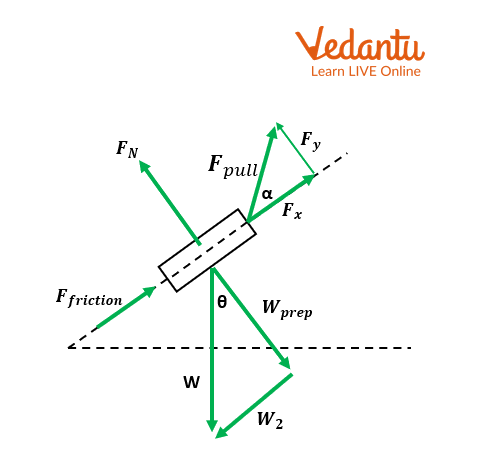
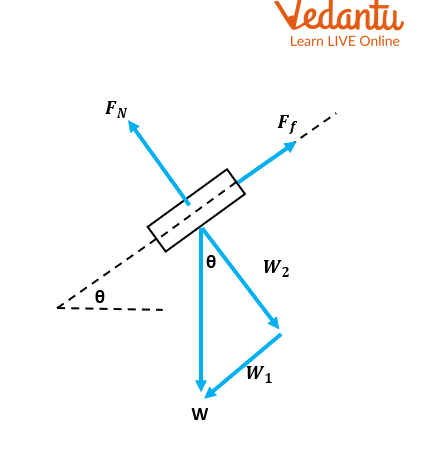
1. A block being driven DOWN an inclined plane by a force parallel to the incline should have its complete free-body diagram drawn. Assume that the slope is NOT frictionless and has an angle of inclination of θ degrees.

Ans.

2. On an inclined plane with a 10o of inclination, a 100 kg block is positioned. Find:

1. the parallel and perpendicular components of the gravitational force.

2. The normal force 

3. the amount of friction keeping the block in place.

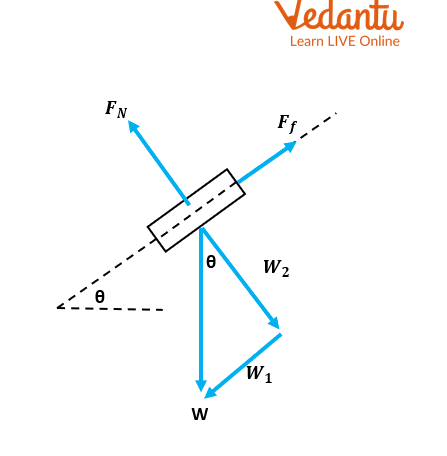
Ans. \[W = mg = 100kg.(9.8m/{s^2}) = 980N\]

\[{W_1} = W.\sin \theta  = 100kg.(9.8m/{s^2}).\sin (10) = 170.2N\]

\[{W_2} = W.\cos \theta  = 100kg.(9.8m/{s^2}).\cos (10) = 965.1N\]

\[{F_f} = {W_1} = 170.2N(uphill)\]

\[{W_2} = 965.1N\]

3. The parking brake is engaged on a 1000 kg car that is parked on a 20° slope. Find the amount of pressure the brake has to exert to stop the car and also find the typical force acting on the automobile.

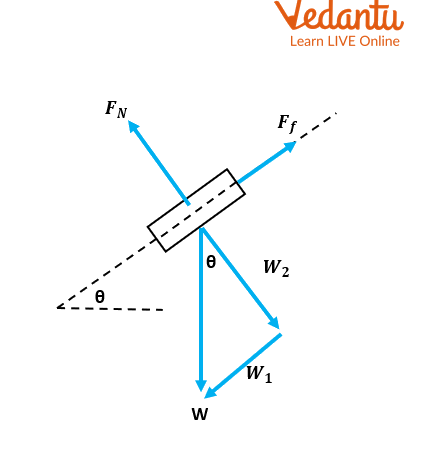
Ans. \[W = mg = 100kg.(9.8m/{s^2}) = 980N\]

\[{W_1} = W.\sin \theta  = 1000kg.(9.8m/{s^2}).\sin (20) = 3351.8N\]

\[{W_2} = W.\cos \theta  = 1000kg.(9.8m/{s^2}).\cos (20) = 9209N\]

\[{F_{brakes}} = {W_1} = 3351.8N(uphill)\]

\[{F_N} = {W_2} = 9209N\]

4. On a 25o inclined plane, a 4 kg block is placed. Calculate the acceleration of the box assuming a frictionless surface.

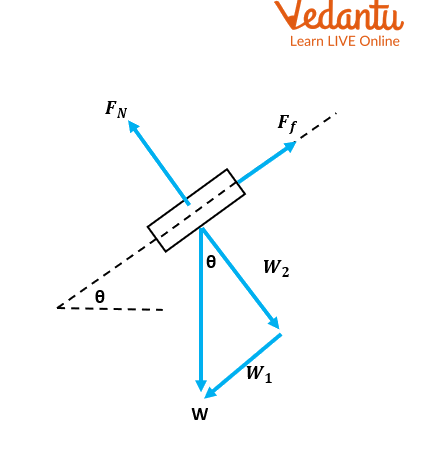
Ans. ${W = mg = 4kg.(9.8m/{s^2}) = 39.2N\ }$

${W_1 = w. \sin (\theta) = m.g. \sin (\theta) = 4 kg .(9.8). \sin (25) = 16.6 N}$

${{F_f} = 0(frictionless) }$

${{F_{net}} = {W_1} - {F_f} = 16.6N(downhill) }$

${{F_{net}} = ma }$

${16.6N = 4kg.a }$

${a = 4.2m/{s^2}(downhill) }$

5. An incline has a changeable inclination angle. After placing a 20 kg block on the slope, the angle is raised until the block starts to slide. Determine the angle at which the block slides if the block and the incline have a coefficient of static friction of 0.6.

Ans. ${W_1 = w. \sin (\theta) = m.g. \sin (\theta)}$

${F_{fstatic} = \mu_s.F_N}$

${F_N = W_2 = m.g. \cos (\theta) }$

${F_{fstatic} = \mu_s.F_N = \mu_s  m.g. \cos (\theta) }$

when the box begin to slide, it becomes

${W_1 > f_{static}}$ 

${mg\sin \theta  > {\mu _s}mg\cos \theta \\}$

${sin \theta  > {\mu _s}\cos \theta \\}$

${\frac{{{\mathop{\rm Sin}\nolimits} \theta }}{{\cos \theta }} > {\mu _s}\\}$

${\theta  = {\tan ^{ - 1}}({\mu _s})\\}$

${\theta  = {\tan ^{ - 1}}(0.6)\\}$

${\theta  = 31^\circ }$

6. Why isn't an inclined plane 100% effective?

Ans. It is because some of the input work is used to overcome friction, the output work is always less than the input work. As a result, efficiency is never 100%.

7. Why does a inclined plane reduce function?

Ans. Moving an object is much simpler when using an inclined plane. When moving something up an inclined plane, it requires less force than when lifting something straight up. Due to the ramp's mild slope, less force is required, but a greater distance must be travelled with the weight.

8. What benefits do inclined planes offer us?

Ans. In order to load and unload cargo into trucks, ships, and aeroplanes, inclined planes are frequently utilised in the form of loading ramps. By leveraging the normal force of the plane to offset the gravitational force, inclined planes also enable the safe vertical descent of large, fragile objects, including people.

9. What are wedges and inclined planes?

Ans. Simple machines like inclined planes assist disperse the force needed to complete a task. Two forms of inclined planes that typically require movement to function are wedges and screws. Like a knife, wedges typically concentrate force in order to divide or cut through objects.

10. How can the net force on an inclined plane be determined?

Ans. Because the two forces acting on the body are not in opposing directions, it is challenging to calculate the net force acting on an item on an inclined plane. It will be easier to add other forces operating on the item if one of the forces acting on it can be broken down into perpendicular components.

Practical Based Questions

1. A man is facing the engine of a moving train. When he throws a coin, it lands behind him. The train is

1. travelling forward at a constant rate.

2. accelerating forward motion

3. going backwards at a constant speed.

4. travelling slowly forward.

Ans:  [B] Accelerating forward motion

2. Where does the reaction to a jet plane flying in the atmosphere come from?

1. Atmosphere and gravity

2. Atmosphere

3. Gravity

4. Gases ejected by the plane

Ans: [D] Gases ejected by the plane

3. What is being measured by the ratio of force and acceleration?

1. Momentum

2. Impulse

3. Velocity

4. Inertia

Ans: [D] Inertia

4. In which principle of conservation, rocket works,

1. Momentum

2. Mass

3. Energy

4. All of the above

Ans: [A] Momentum

5. A wire cage with a bird inside is suspended from the spring balance. Let W1 be the spring balance's reading. The spring balance's readout becomes W2 if the bird flaps around inside the cage. Which statement is accurate?

1. W1=W2

2. W1>W2

3. W1<W2

4. None of the above

Ans: [B] W1>W2

6. A body must be pulled down from an inclined plane after being placed there. The typical reaction's angle with the vertical will be

1. equal to the friction angle.

2. greater than the friction angle

3. equal with the angle of repose

4. less than the angle of repose

Ans: [D] less than the angle of repose

7. Friction can be reduced by lubrication because

1. The liquid and solid are moving relative to one another.

2. The limiting friction laws do not apply.

3. Lubricant molecules make a thin film which reduces the friction.

4. None of the above.

Ans: [C] Lubricant molecules make a thin film which reduces the friction

8. Sometimes, a car will flip while turning. When it turns over, it is

1. The first wheel to lift off the ground is the inner wheel.

2. The first wheel to lift off the ground is the outer wheel.

3. Both wheels lift off the ground at the same time.

4. Either of the wheels lifts off the surface first.

Ans: [A] The first wheel to lift off the ground is the inner wheel

9. On a stretched telegraph wire, a bird detaches. The additional tension that the wire experiences is

1. zero.

2. equal to the bird's weight.

3. more than the bird's weight.

4. less than the bird's weight.

Ans: [C] more than the bird’s weight

10. which of the following options talks about self-adjusting force

1. Static friction

2. Dynamic friction

3. Limiting friction

4. Sliding friction

Ans: [A] Static friction

Conclusion

Starting at zero degrees of inclination, the value of mgsinθ grows, and the frictional force increases in step with it. Therefore, we do not need to apply any tension to the string until the limiting friction W = 0.

Further tilting the angle causes net tension in the string to need to balance \[mg\sin \theta  - {f_r}\]  or else the roller will fall faster.

It is challenging to calculate W's precise value. In order to help, we can:

When the roller is just about to roll down tension \[{W_1} < W\] and just about to roll up tension \[{W_2} > W\], respectively.

So, ${W=\dfrac{{W}_{1}+{W}_{2}}{2}}$