To Study the Effect of Load on Depression of a Suitably Clamped Meter Scale

Buckling (depression) is defined as a sudden change in shape (deformation) of a structural component under loads, for instance, a column bowing under compression or a plate wrinkling under shear. When a structure is subjected to a gradually increasing load, a constituent may suddenly change shape, and the structure and component are said to have buckled.

Even if the stresses that develop in the structure are well below those required to cause a fault in the material of which the structure is composed, depression (buckling) may occur. Further loading may result in significant yet unexpected deformations, potentially resulting in the constituent's complete loss of load-carrying capacity. Nevertheless, if the deformations induced by depression do not end up causing the constituent to collapse completely, the constituent will continue to bear the load that caused it to buckle. If the depressed constituent is part of a larger assemblage of components, such as a building, any additional load applied to the structure's buckled portion will be redistributed.

An axial load is applied to a column when it is used through the center of gravity (centroid) of its cross-section. An eccentric load is a load that occurs at any other point in the cross-section.

Table of Contents:

• Aim 

• Apparatus Required

• Theory 

• Procedure 

• Observations

• Calculations

• Result.

• Precautions

• Sources of Error.

• Lab Manual Question

• Viva Questions

• Practical Based Questions

Aim

To study the effect of load on depression of a suitably clamped meter scale loaded at (i) its end (ii) in the middle.

Apparatus Required

• A straight, uniform wooden meter rod (scale)

• Two G clamps 

• Pointer pin 

• A thread

• 50 g slotted weights

• Wax

• A vertical scale

• A clamp stand.

Theory

The depression (buckling) is $\delta$ caused by the load in the wooden rod of the length 'l'.

$\delta=\dfrac{mgl^{3}}{4Ybd^{3}}$

Where, 

m= total mass of slotted weights

Y= young’s modulus

b=breadth

d=depth

From the above-mentioned formula it can be said that for a given rod,

$\delta\ltimes~mg$

This implies that the depression created is proportional to the weight (load) suspended from one end.

Diagram: The clamp stand diagram is given below.

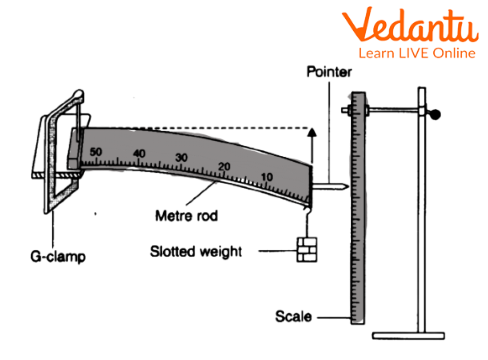
Effect of load on depression of a suitably clamped meter scale

Procedure

(i) When one end of the meter scale is loaded:

• Secure the meter scale with a G-clamp at one edge of a table corner, ensuring that it remains straight in the horizontal plane.

• At the free end of the meter scale, the pointer pin or needle should be wax-attached (a student needs to take 50g wax).

• Place the scale vertically on a stand to take readings.

• When no weights are suspended, the first reading on the vertical scale corresponds to the pointer's tip.

• Using a strong thread, suspend the weights in steps at the free end of the meter scale and record the corresponding measurements on the vertical scale.

• Start unloading the weights one at a time after 56 readings, acknowledging the reading on the scale each time.

(ii) When the meter scale is center-loaded:

• To find the C.G. of the meter scale, suspend it with a thread.

• Set the meter scale symmetrically on two knife edges 85 cm apart and check that it is perfectly horizontal.

• A pointer is waxed or taped to the scale's middle point to take the reading.

• Steps 3-6 should be reiterated, and observations should be noted in the table.

Observations

Initial pointer reading on a vertical scale without loading at the free end = $x_0=...cm$

Load and Depression Table When Meter ROD is Loaded at its End

Initial pointer reading on a vertical scale without loading in the middle=$x_0=...cm$

Load and Depression Table When Meter ROD is Loaded in the Middle

Graph:

Make a graph with a load on the X-axis and depression on the Y-axis for both cases. In both cases, the graphs form a straight line, as illustrated below.

Graph of load and depression

Result

The graphs of load and depression are straight lines, indicating that depression is proportional to load.

$\delta\ltimes~mg$

Precautions

• The meter scale must be linear and uniform and locked in place.

• The pointer's tip should not keep in touch with the vertical scale.

• The scale's elastic limit should not be exceeded.

• Meter scale readings should be taken with caution.

Sources of Error:

• The meter scale may be uneven.

• The pointer's tip may not be very sharp.

Lab Manual Questions 

1. Why is a pointer attached to the scale's midpoint or at the free end of the meter rod with wax or adhesive tape?

Ans: It is done to take the reading.

2. What will happen if the scale is loaded beyond its elastic limit?

Ans: It will undergo permanent deformation.

3. What do you mean by elastic limit?

Ans: It is the maximum stress that a material can endure before permanently deforming.

Viva-Based Questions

1. What do you mean by Young’s modulus?

Ans: It is a material property that explains how easily it can extend and deform and therefore is defined as the tensile stress to tensile strain ratio.

2. What is stress?

Ans: Stress is the force acting on a material's unit area.

3. Explain the similarity between a stress-strain curve and a load-depression graph.

Ans: The nature of both graphs is a straight line.

4. How will you define Plasticity?

Ans: The property of a body that does not resist the deforming force applied and causes the body to be permanently deformed.

5. What is a center of gravity?

Ans: It is the imaginary point at which the body's weight appears to be accumulated.

6. What is the purpose of this experiment?

Ans: To understand the effect of load on depression. 

7. What is the use of a clamp during the experiment?

Ans: To lock the meter scale in one place.

8. Explain Hooke’s law.

Ans: A law that states the strain in a solid is proportional to the applied stress only within the solid's elastic limit.

9. State two disadvantages of Hooke’slaw.

Ans: Hooke's law isn't a universal law and is only applicable in the elastic region.

10. What exactly is the distinction between load and effort?

Ans: A load is a large or heavy object that demands effort to move or lift. An effort is a force applied to cause the desired shift in the position of the load.

Practical-Based Questions

1. What type of load will be when the metering rod is loaded at its center/centroid?

(a) Radial

(b) Axial

(c) Both (a) and (b)

(d) None of the above.

Answer: (b) Axial

2. When a body fully regains its former size and shape after being subjected to an external deforming force, it is referred to as

(a) A deformed body.

(b) Perfectly elastic body.

(c) Perfectly plastic body.

(d) None of the above.

Answer: (b) Perfectly elastic body.

3. When a load is removed, a material's ability to return to its former size or shape is referred to as

(a) Viscosity

(b) Elasticity

(c) Plasticity

(d) None of these

Answer: (b) Elasticity

4. A material's malleability is its

(a)Ability of a material to experience significant, long-lasting deformations in tension.

(b)The capacity of a material to experience significant, long-lasting compressive deformations.

(c)The ability of a substance to regain its original size and shape after being subjected to a deforming force

(d)None of the above.

Answer: (b)The capacity of a material to experience significant, long-lasting compressive deformations.

5. Which of the following physical quantities best describes stress?

(a) Impulse/volume

(b) Restoring force/area

(c) Force/length

(d) Energy/area

Answer: (b) Restoring force/area

6. Select the physical quantity that is a unit less.

(a) Young’s modulus

(b) Strain

(c) Pressure

(d) Stress

Answer: (b) Strain

7. Young's modulus is the ratio of the normal stress to the

(a) Longitudinal stress within acceptable bounds.

(b) Stress along a length as a yield point.

(c) Within the elastic limit, normal strain.

(d) Reciprocal of the elastic limit's normal strain.

Answer: (c) Within the elastic limit, normal strain.

8. By placing a load on the free end of the spring, it can be stretched. The spring is under strain due to:

(a) Shear

(b) Volumetric

(c) Longitudinal and shear

(d) Longitudinal

Answer: (c) Longitudinal and shear

9. Hooke's law describes which property?

(a) Elasticity

(b) Plasticity

(c) Both (a) and (b)

(d) None of the above.

Answer: (a) Elasticity

10. What is the CGS unit of stress?

(a) $Dyne~cm^{-2}$

(b) $Dyne~m^{2}$

(c) $N~cm^{-2}$

(d) None of the above.

Answer: (a) $Dyne~cm^{-2}$

Conclusion

Whenever the load (loading) on the metal rod increases, depression also increases. Similarly, a decrease in the load (unloading) leads to decrement in depression. This establishes a linear relationship between load and depression, resulting in the graph forming a straight line. Thus, load and depression are directly proportional to each other.