CBSE Physics Experiment To Find the Force Constant of a Helical Spring

Of all the things we use daily – such as computer keyboards, pens, clocks, door handles, kitchen toasters – involve the use of springs. Therefore, it becomes essential to know about the force constant of spring and the spring’s elastic limit.

Following is a simple experiment aimed at finding the force constant of a helical spring by studying the load versus elongation graph for four wires.

Table of Contents

• Aim

• Theory

• Apparatus Required

• Procedure

• Observations

• Result

• Precautions

Aim

To find the force constant of a helical spring by studying the graph between force and displacement.

Theory

In the constant spring experiment, we will be using Hooke’s law, where the force exerted by spring can be given as

\[F =  - kx\]

to determine the spring constant of given springs by plotting a graph between the force applied on them and their respective displacements from the inverse slope of the graphs. We’ll be doing this for four springs made up of different materials to analyse whether the spring constant obtained has any material dependence (like that of the modulus of elasticity).

Apparatus Required

• A rigid support

• Four springs of different materials, each having a length of about 50 cm and diameter of about 3 cm

• A light hanger with hook

• Six small slotted weights in steps of 100g

• A vertical wooden scale

• A fine pointer

Procedure

1. Suspend the first spring from a rigid support and attach the light hanger with a hook with its free end. Attach the pointer with a hanger.

2. Arrange the wooden scale vertically such that the spring with its pointer overlaps with the markings on the scale. Tabulate the displacement by looking at the pointer with the scale against zero loads.

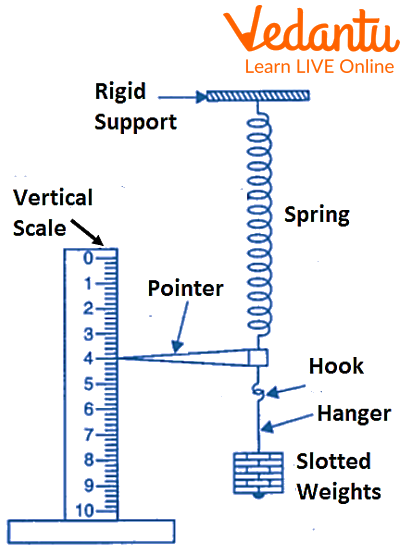
Experiment Apparatus to Find the Force Constant of Helical Spring

3. Gently add the lightest load of 100g into the hanger. Wait for the spring to stabilise its position against the scale.

4. After the spring stops oscillating, note the reading on the scale against the fine pointer.

5. Add a load of 100 g into the hanger and again note the reading after spring comes to rest. Repeat the procedure for all loads. Tabulate the observations.

6. Now start decreasing the loads in the steps of 100g. Similarly note the displacements each time.

7. Repeat the procedure for other springs as well. Tabulate in four observation tables.

Observations

Least count (LC) of the wooden scale = 

Observation Table

Graph

Plot a graph with the load applied on the x-axis and the displacement corresponding to the load along the y-axis for each spring. It will be a straight line passing through the origin in each case. This line's inverse slope gives the absolute value of the spring constant for each spring.

Slope, \[m = \dfrac{y}{x} = \dfrac{\text{Displacement (x)}}{\text{Load applied (F)}}\]

\[\Rightarrow m = \dfrac{x}{F}\] and since \[\left| F \right| = k\left| x \right| \to k = \dfrac{{\left| F \right|}}{{\left| x \right|}} = \dfrac{1}{m}\]

\[\Rightarrow k = \dfrac{1}{m}\]

Use the units of displacement x in meters (m), and the load applied as the product of masses applied in kilograms (kg) and the acceleration due to gravity (\[g = 9.8\;m{s^{ - 2}}\]) in newtons (N).

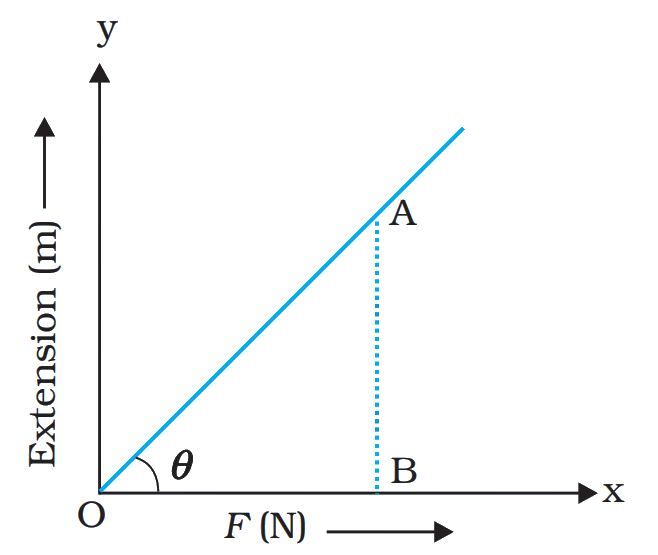
Load-extension Graph

Result

From the graphs obtained

1. The spring constants (in\[N/m\]) for each spring are as follows:

1. For spring-1, \[{k_1} = ..........\;N/m\]

2. For spring-2, \[{k_2} = ..........\;N/m\] 

3. For spring-3, \[{k_3} = ..........\;N/m\] 

4. For spring-4, \[{k_4} = ..........\;N/m\] 

2. The spring constants obtained are nearly the same for each spring made of specific material. Therefore, the spring constant is independent of the material of the spring.

Precautions

1. The springs should be rigidly fixed and should not jerk.

2. Readings must be noted only after the spring stops oscillating after adding load.

3. Loading the spring with a very light/hefty load should be prevented.

4. Displacement should be carefully noted, corresponding to the fine pointer.

5. Displacement of the spring corresponding to zero loads must be subtracted from the displacements in the presence of load.

Lab Manual Questions

1. What is the effect on the spring constant of spring if we alter the thickness of the wire, keeping the mass of the load the same?

Ans: The spring constant is directly proportional to the thickness of a wire. This is because a thicker wire will oscillate with a lesser time period, owing to a more spring constant value.

2. Enlist the factors affecting the spring constant of a given spring.

Ans: Spring constant of a given spring depends on the following factors:

1. Softness/ hardness (or the stiffness) of the material.

2. Thickness of the wire of the spring.

3. Turn the density of the coil.

4. Length of the spring.

3. How is the period of oscillation of a spring related to its stiffness?

Ans: A spring with a larger spring constant value will have more stiffness. As a result, it will extend/ compress by a smaller distance and consequently have a short time.

4. If you are given a spring with a known spring constant of 100 N/m, what does it imply physically?

Ans: In such a case, its physical implication would be that it takes exactly 100 N of force to stretch/compress that spring by 1 meter.

Viva Questions

1. How does the force constant depend on the loaded weights?

Ans: The force constant is independent of the mass of loaded weights. It is only a characteristic of the material.

2. Why must spring have a uniform turn density?

Ans: This is because the force constant of a spring depends upon turn density and increases with the increase in turn density, i.e., the number of turns per unit length.

3. How does the spring constantly change with the length of the spring?

Ans: The spring constant of a spring is inversely proportional to the length of the spring.

4. What are the SI and CGS units of force constant?

Ans: The SI unit of force constant is Newton per metre (N/m) while its CGS unit is dyne per centimetre (dyne/cm).

5. Why should we wait for some time after removing a weight?

Ans: We should wait because it takes some time for the wire to reach a steady state. 

6. Why should we remove kinks before starting the experiment?

Ans: If we do not remove kinks, they get opened up by the load and show more wire extension.

7. What is elastic fatigue?

Ans: The quick drying-out of vibrations due to prolonged oscillations is known as elastic fatigue.

8. What is the elastic after-effect?

Ans: Elastic after-effect is defined as the tendency of the strain to persist for some time after the stress removal.

9. Calculate the work done when an object of mass m falls vertically on the free end of a spring from a height h and compresses the spring by a distance x. Take the spring constant of the spring to be k.

Ans: Work done by the gravitational force,\[{W_g} = mg(h + x)\]

Work done on the spring to compress it,\[{W_S} =  - \dfrac{1}{2}k{x^2}\]

Hence total work done,\[{W_g} + {W_S} = mg(h + x) - \dfrac{1}{2}k{x^2}\]

10. How is stress measured?

Ans: Stress is measured by the external deforming force applied per unit area within the elastic limit.

Practical Based Questions

1. A leaf spring is

1. A closely coiled spring

2. A beam of uniform geometry

3. A beam of uniform strength

4. A bar of uniform strength

Ans: (C) A leaf spring is a beam of uniform strength.

2. The maximum shear stress for helical spring is inversely proportional to:

1. Thickness of spring

2. Square of radius of spring

3. Pitch of helical spring

4. Amount of stress applied

Ans: (A) The maximum shear stress for helical spring is inversely proportional to the thickness of spring.

3. .......... spring is used to absorb shocks and vibrations.

1. Torsion

2. Leaf

3. Disc

4. Conical

Ans: (B) Leaf spring is used to absorb shocks and vibrations.

4. Stiffness of a spring is defined as the load required per unit ............ .

1. Area

2. Volume

3. Height

4. Deflection

Ans: (D) Stiffness of spring is defined as the load required per unit deflection.

5. Tick the correct option on which the spring constant of a helical compression is independent:

1. Material strength

2. Wire thickness

3. Coil diameter

4. Turn density

Ans: (A) The spring constant of a helical compression is independent of material strength.

6. If a coil is cut into two halves, the stiffness of cut coils will be:

1. Double

2. Half

3. Same

4. None of the above

Ans: (A) If a coil is cut into two halves, the stiffness of cut coils will get doubled as it is inversely proportional to length.

7. In SI units, force constant is expressed in:

1. \[Dyne/cm\]

2. \[N/m\]

3. \[Lb/{s^2}\]

4. None of these

Ans: (B) In SI units, force constant is expressed in \[N/m\].

8. Potential energy possessed by a spring is called:

1. Compressive

2. Deflection

3. Elastic

4. Extensive

Ans: (C) The potential energy possessed by a spring is called elastic potential energy.

9. If a spring of spring constant k compresses by a distance x due to an applied force F, then the potential energy stored in the spring is given by:

1. \[\dfrac{{2x}}{{{F^2}}}\]

2. \[\dfrac{{{F^2}}}{{2k}}\]

3. \[\dfrac{{2k}}{{{F^2}}}\]

4. \[\dfrac{{{F^2}}}{{2x}}\]

Ans: (B) Since \[\left| F \right| = kx\;\;\; \to \;\;\;\;x = \dfrac{F}{k}\]

So potential energy = \[\dfrac{1}{2}k{x^2} = \dfrac{1}{2} \times (kx) \times (x)\]

\[ = \dfrac{1}{2}k{x^2} = \dfrac{1}{2} \times F \times \dfrac{F}{k}\]

\[ = \dfrac{{{F^2}}}{{2k}}\]

10. Within the elastic limit, how would the potential energy stored in a spring change if it is compressed to twice the displacement?

1. Will remain unchanged

2. Increase by\[100\% \]

3. Increase by\[400\% \]

4. Increase by\[900\% \]

Ans: (C) The potential energy U of a spring is given by:

\[U = \dfrac{1}{2}k{x^2} \propto {x^2}\]

where F is the external force applied and x is the corresponding displacement in the spring. Since U depends on the square of x, hence doubling x will increase U by 4 times or \[400\% \].

Conclusion

From this experiment, we can conclude that the role of springs and Hooke’s law is indispensable in our society – from pens, switches, keyboards, and door handles to big-scale safety equipment such as the pillars used in a building, railway tracks and bridges.

In this experiment, we discussed the spring constant of a spring and studied a simple hands-on to study the relationship of the same in accordance with Hooke's law.

We hope that the reader has gotten some valuable insight into the topic from this experiment and that the article inspired him to further explore the topic in physics for the times to come.