To Study the Dissipation of Energy of a Simple Pendulum by Plotting a Graph Between Square of Amplitude and Time

Introduction

One of the most popular applications for pendulums is to tell time. A pendulum inside a clock can maintain accurate timekeeping because its motion occurs at constant intervals of time. Also, the pendulum is used to gauge the gravitational effect because the force of gravity causes it to swing back toward its average position.

In this class 11 physics experiment, we'll talk more about a simple pendulum and how we can calculate the dissipation of energy of a simple pendulum.

Table of Content

• Aim

• Working of Simple Pendulum

• Result

Aim

To study the dissipation of energy of a simple pendulum by plotting a graph between the square of the amplitude of a simple pendulum and time.

Working of Simple Pendulum

The bob, or heavy point mass, of a basic pendulum is suspended from rigid support by a massless thread that cannot be extended. The pendulum is started when the bob is pulled to one side from its mean position and then released; the bob then alternately swings to the opposite side of its mean position. 

The pendulum oscillates back and forth, accelerating and decelerating. According to Newton's Second Law of Motion, as an object speeds up or decelerates, it creates force, which we can observe when the pendulum pulls on the string.

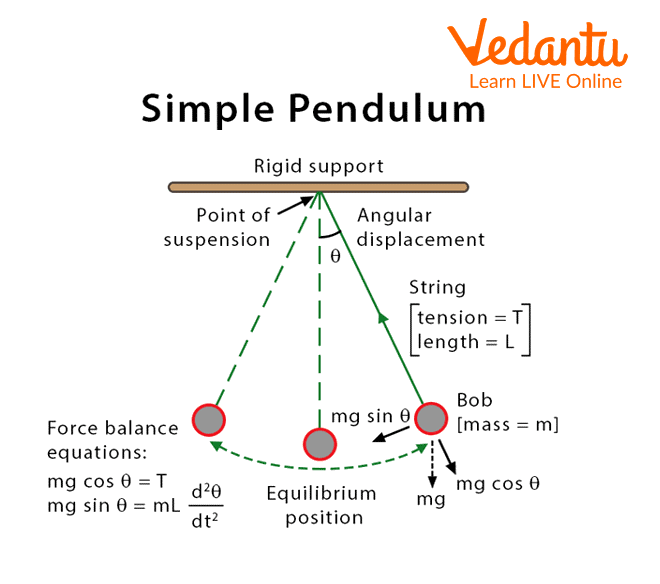
A Simple Pendulum

Galileo’s Principle

Galileo was the first to study the unique characteristics of a pendulum. Each pendulum, according to Galileo, has a fixed period. A pendulum's period is the time it takes to complete one oscillation or to swing back to its starting point. 

Apparatus Required

• A pendulum bob

• a split cork

• thread 

• metre scale 

• a clamp stand 

• stopwatch

• chalk piece

Theory

The restoring force F for a simple pendulum moving in simple harmonic motion is given by F(t) = -kx (t),

where x (t) represents the displacement at time t and k is a quantity known as the force constant (spring constant), k =mg/L. The negative sign shows the direction of F is towards the mean position. 

The displacement is x (t) = A₀ cos (ωt – θ), where ω is the (angular) frequency and θ is a constant. A₀ is the maximum displacement in each oscillation, which is called the amplitude.

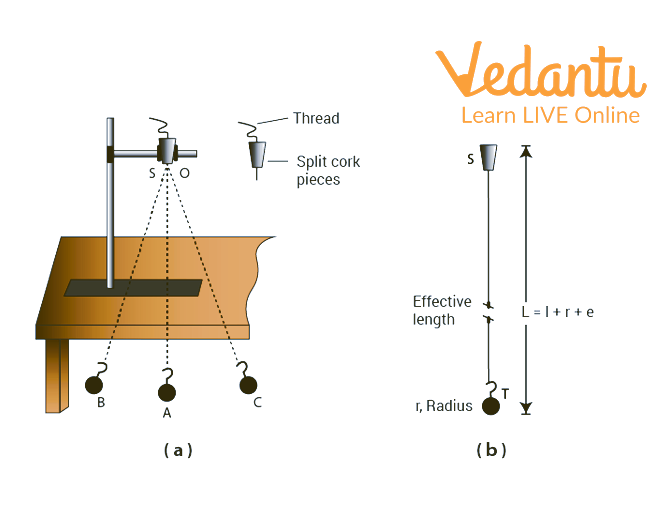
A Simple Pendulum and Length of a Pendulum.

The total energy of the pendulum, E₀ = ½ k A₀². The total energy remains constant in an ideal pendulum because its amplitude remains constant. 

However, the amplitude is not constant in a simple pendulum. It depends on time and decreases with time because of reasons like air resistance, imperfections in the rigidity of the string and suspension, etc. Therefore, in each succeeding oscillation, A₀ amplitude decreases over time. 

The total energy of the pendulum is E(t) = ½ kA(t) = E₀ e⁻ᵗ. Thus, the energy reduces with time because some energy is lost to the surroundings. A damped oscillator's frequency is mostly independent of its amplitude. As a result, we can measure the number of oscillations ($n$) in addition to the time. T is the period, and after n oscillations, t = nT. ‘$E_n$’ is the energy of the oscillator at the end of ‘n’ oscillations and can then be expressed in the form Eₙ = E₀e⁻ᵅⁿ.

Procedure

1. Find the bob's mass ‘m’ using physical balancing.

2. As shown in the diagram, take a cotton thread that is about 150 cm long, tie the bob to one end, and then pass the other end through a split cork to make the pendulum's effective length 130 cm. The effective length of the pendulum is equal to (the radius of the bob + the length of the hook of the bob-pendulum + the length of the thread). Clamp the two halves of the cork together tightly.

3. Now position the stand on the table so that the bob is 1 to 2 cm or so above the surface.

4. Just below the bob, place a metre scale so that a complete scale division is below the bob's centre.

5. Release the bob by moving it 5 cm away from its resting position (mean position) along the metre scale. The bob begins to vibrate about the mean position A, and as time goes on, you'll see that its amplitude lowers.

6. Set the bob to its mean position A (stop position). Find the stopwatch's lowest count.

7. Return the bob to the rest position A on the metre scale and move it 5 cm away before releasing it to have it vibrate in the same vertical plane.

8. When the bob is in its most extreme right position, start the stopwatch, mark the bob's location on the metre scale, and enter this time as zero.

9. Keep a watch on the bob's movement continuously, measuring its amplitude and keeping track of time after each alternative oscillation (i.e., 0, 2, 4, 6, etc.) until the amplitude falls to about 1 cm.

10. Record 10 observations in the table.

11. Create a graph by putting time (t) along the X-axis and the amplitude square ($A^2$) along the Y-axis.

Observations

Mass of the bob by physical balance is = ……(g) =..... x 10⁻³ kg.

The least count of a stopwatch is = ….. Sec

Mass of the pendulum bob m= ….g

Radius (r) of the simple pendulum bob = ... cm

Length of pendulum l = …..cm = ….m.

Force Constant kg = mg / l = ….. Nm⁻¹ 

Initial amplitude, A₀ = ... cm 

Initial energy which is equal to, $E_0$ = 1/2 (k ${A_o}^2$ ) = ... J

Table for the dissipation of Energy

Result

For a simple pendulum the graph between the square of the amplitude with respect to time is drawn. The graph displays the simple pendulum's energy dissipation over time.

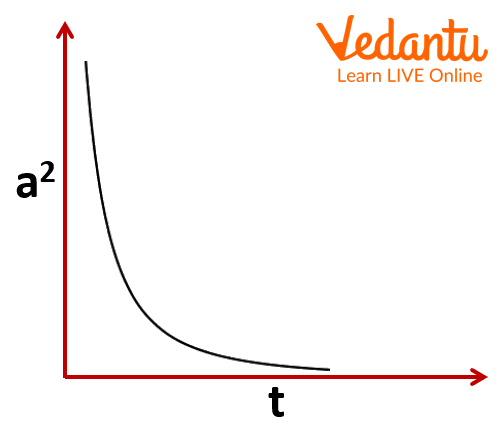
The Graph Between Square of Amplitude and Time.

Precaution

1. Support for the pendulum should be rigid.

2. It is best to keep the amplitude small.

3. The pendulum should have enough length (about 2 metres).

4. Pull on a string to prevent the metallic block from spinning.

5. The centre of the block's bottom should be taped with paper.

Lab Manual Questions

1. What is a simple pendulum? A pendulum clock uses a pendulum, but is it a simple pendulum? Justify your response.

Ans. It consists of a heavy point mass suspended from a rigid support by a massless, inextensible thread. The pendulum in the pendulum clock is not simple because it is an ideal example. Hence the answer is no. Given that it is the size of a point and has no mass, the mass cannot be heavy.

2. What is the time period?

Ans. The time period refers to the amount of time it takes a freely oscillating pendulum to complete one oscillation. Second is its SI unit (s).  It is the reciprocal of oscillation frequency.

3. What do you mean by amplitude?

Ans. The maximum deviation of the bob from its equilibrium position is the amplitude of a simple pendulum. SI unit of amplitude is metre (m). The pendulum hangs straight down while it is at rest, not swinging.

4. A simple pendulum is oscillating with an amplitude having angular velocity ω. What will be the ratio of kinetic energy to potential energy at displacement x from the mean position?

Ans. The velocity of a particle in S.H.M is given by

v= ω A²-x²,   where x is the displacement from the mean position

Therefore, K.E = ½ mv² = ½ mω² (A²-x²).....(i)

P.E = ½ kx² = ½ (mω²)x² …….(ii)

From (i) and (ii) we get, 

The ratio of K.E/ P.E = (A²-x²)/ x².      

Viva Questions

1. How will the time period change if the bob's mass is increased?

Ans. Time does not depend on the mass of the bob; instead, the time period remains unaffected.

2. What is energy expressed in SI units?

Ans. The joule is the same SI unit for energy as it is for work (J).

3. What is kinetic energy?

Ans. Kinetic energy is the force that causes motion, which can be seen in the movement of a particle, an object, or a group of particles. Any moving item uses kinetic energy, such as a person walking, a baseball being thrown, a piece of food falling from a table, or a charged particle in an electric field.

4. What is the relation between damping force and the velocity of the bob?

Ans. The damping force on an oscillator is directly proportional to the velocity of the bob.

5. How does the length of the pendulum affect the simple pendulum's time period?

Ans. The time period varies with the pendulum length because it is directly proportional to the square root of the pendulum length. 

6. Why would the amplitude be small in a simple pendulum experiment?

Ans. The angular displacement of the bob used in a basic pendulum is small when the vibrating pendulum's amplitude is small. The restoring force, in this case, is F= mgsinθ =mgθ =mgx/l, where x is the bob's displacement and l is the pendulum's length. Thus, F ∝ x, F is directed towards the mean position, hence if θ is small, the motion of the bob in a simple pendulum will be SHM.

7. What is the mechanical energy conservation principle?

Ans. According to the conservation of mechanical energy principle, a body or system's mechanical energy stays constant if it is only subjected to conservative forces.

8. Why does the amplitude of a simple pendulum decrease during the vibratory motion of the pendulum?

Ans. The amplitude of a simple pendulum decreases during the vibratory motion of the pendulum due to friction due to air. 

9. What do you mean by the energy of a simple pendulum?

Ans. Mechanical energy is conserved in a simple pendulum with no friction. Kinetic energy and gravitational potential energy combine to make up total mechanical energy. Kinetic energy and gravitational potential energy are constantly exchanging as the pendulum swings back and forth.

10. What will happen to the time of a simple pendulum if it is moved from the equator to the pole of earth?

Ans. The time period will decrease.

Practical Questions

1. What will happen if we double the period of a pendulum,

1. the length will decrease by 2 times 

2. the length will decrease by 4 times

3. the length will increase by 2 times

4. the length will increase by 4 times

Ans. If we double the period of a pendulum, the length is increased 4 times.

2. The velocity has a direct relationship with the damping force acting on an  oscillator. What is the units of the proportionality constant are

1. Kgs

2. Kgms

3. kgs⁻¹

4. kgms⁻²

Ans. As F= -K V, the unit of proportionality is kgs⁻¹.

3. If the oscillation amplitude decreases continuously it is called…….

1. Sustained Oscillation

2. Sinusoidal Oscillation

3. Overdamped Oscillation

4. Underdamped Oscillation

Ans.  If the oscillation amplitude decreases continuously it is called Underdamped oscillation. 

4. What is the oscillation time of the second pendulum?

1. 1 second

2. 2 second

3. 10 second

4. 50 second

Ans. The oscillation time of the second pendulum is 2 seconds.

5. The time periods of the 1 m long pendulum are approximately equal...

1. 6s

2. 4s

3. 2s

4. 1s

Ans. The time periods of the 1 m long pendulum are approximately equal to 2s.

6. The time period of one oscillation for a simple pendulum is given by

1. 2 π √ g/l

2. 2 π √ 2l/g

3. 2 √ l/ 2g

4. 2 π √ l/g

Ans. The time period of one oscillation for a simple pendulum is given by 2 π √l/g.

7. Which of the following has a vibration in S.H.M. that is not a sine curve?

1. Time period

2. Velocity

3. Displacement

4. Acceleration

Ans. In S.H.M., the time period does not have a sine curve.

8. What is the reason for the damping in oscillatory motion?

1. Friction

2. Restoring force

3. Both restoring force and friction

4. Neither friction nor restoring force

Ans. Friction is the reason for the damping in oscillatory motion.

9. If the amplitude of a simple harmonic oscillator is doubled, then

1. its energy is doubled.

2. maximum velocity is doubled.

3. time period is doubled.

4. time period remains the same.

Ans.  If the amplitude of a simple harmonic oscillator is doubled, the time period remains the same. 

10. If the mass of the bob of the pendulum is increased, then the frequency will…

1. Increase

2. Decrease 

3. Remain the same

4. None of these.

Ans. If the mass of the bob of the pendulum is increased, then the frequency remains the same.

Conclusion

We draw the conclusion from this experiment that the energy E of a simple pendulum is directly proportional to the square of amplitude A² (E= ½ k A₀²) and that the amplitude decays with time, leading the energy of the pendulum to dissipate.