Can You See Patterns – CBSE Class 5 Maths Worksheet & Free Solutions PDF
FAQs on Master Patterns: CBSE Class 5 Maths Chapter 7 Worksheet PDF
1. What are patterns?
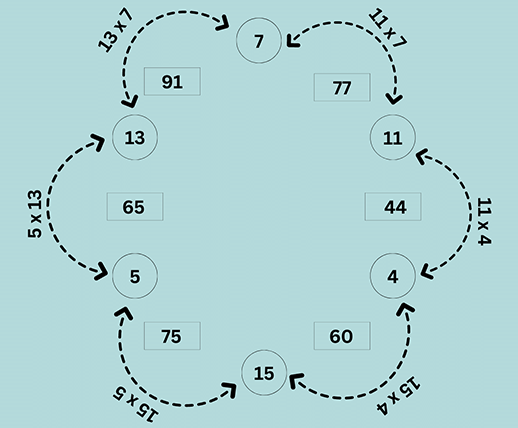
A pattern is formed when there is a repeated arrangement of shapes, numbers, colours, etc. A pattern can be related to any kind of object or event. The set of objects in a pattern is related to each other through a specific set of rules. Patterns are also referred to as sequences.
2. How can I help my child discover patterns?
Students can learn patterns in many different ways, but the key here is to practise as much as they can. The more children practise, the better they are able to understand hidden patterns in things.
Use stickers and stamps - You can create various patterns by using different stickers and stamps. This is an interesting way to teach patterns to kids.
Skip counting - By doing skip counting (in two’s, five’s, etc.), your child can learn addition as well as create different patterns.
Sudoku - Sudoku is a game of number patterns, and by solving simple sudoku, kids can gain a lot of insight into how patterns work.
3. What are different types of number patterns?
Below are listed some of the common number pattern types:
Repeated patterns - When the pattern rule keeps repeating over and over, it is called a repeating pattern.
Growing pattern - If a series of numbers are lined up in a way that they are increasing in magnitude from left to right, then it is a growing pattern.
Shrinking pattern - This is the opposite of the shrinking pattern where numbers decrease as we go from left to right.