ICSE Class 10 Mathematics Chapter 18 Selina Concise Solutions - Free PDF Download
Selina Concise Mathematics Class 10 Solutions Chapter 18 Tangents and Intersecting Chords are undoubtedly an essential study material for the students studying in ICSE Class 10. Vedantu Selnia Solutions provided here along with the downloadable PDF can help the students prepare effectively for their exams. Vedantu Selina Solutions Concise Maths Class 10 Chapter 18 Tangents and Intersecting Chords helps students to get a clear idea about the basic concepts.
The subject experts at Vedantu prepared the ICSE solutions for Class 10 to assist students in preparing for their ICSE board examination. Every step and concept used in solving a solution is explained clearly in the answers provided by Vedantu, leaving no question unsolved. Along with exam preparation, these Vedantu solutions can be used to check if the answers given to the exercise questions by the students are correct while doing their homework and assignments. So, it is advised to all the students to go through these Vedantu Selina Solutions regularly to stand out among the other students in the class and also to excel in the ICSE Board examination of Class 10 exam.
ICSE Class 10 Maths Solutions for Tangents and Intersecting Chords is one of the crucial and most scoring subjects in ICSE Class 10. Vedantu presents solutions for ICSE Class 10 Mathematics which will enable students to score well in the ICSE board examination.
Access ICSE Selina Solutions for Class 10 Mathematics Chapter 18 - Tangents and Intersecting Chords
Very Short A Type
1. The radius of a circle is 8cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10cm from its centre.
Ans:
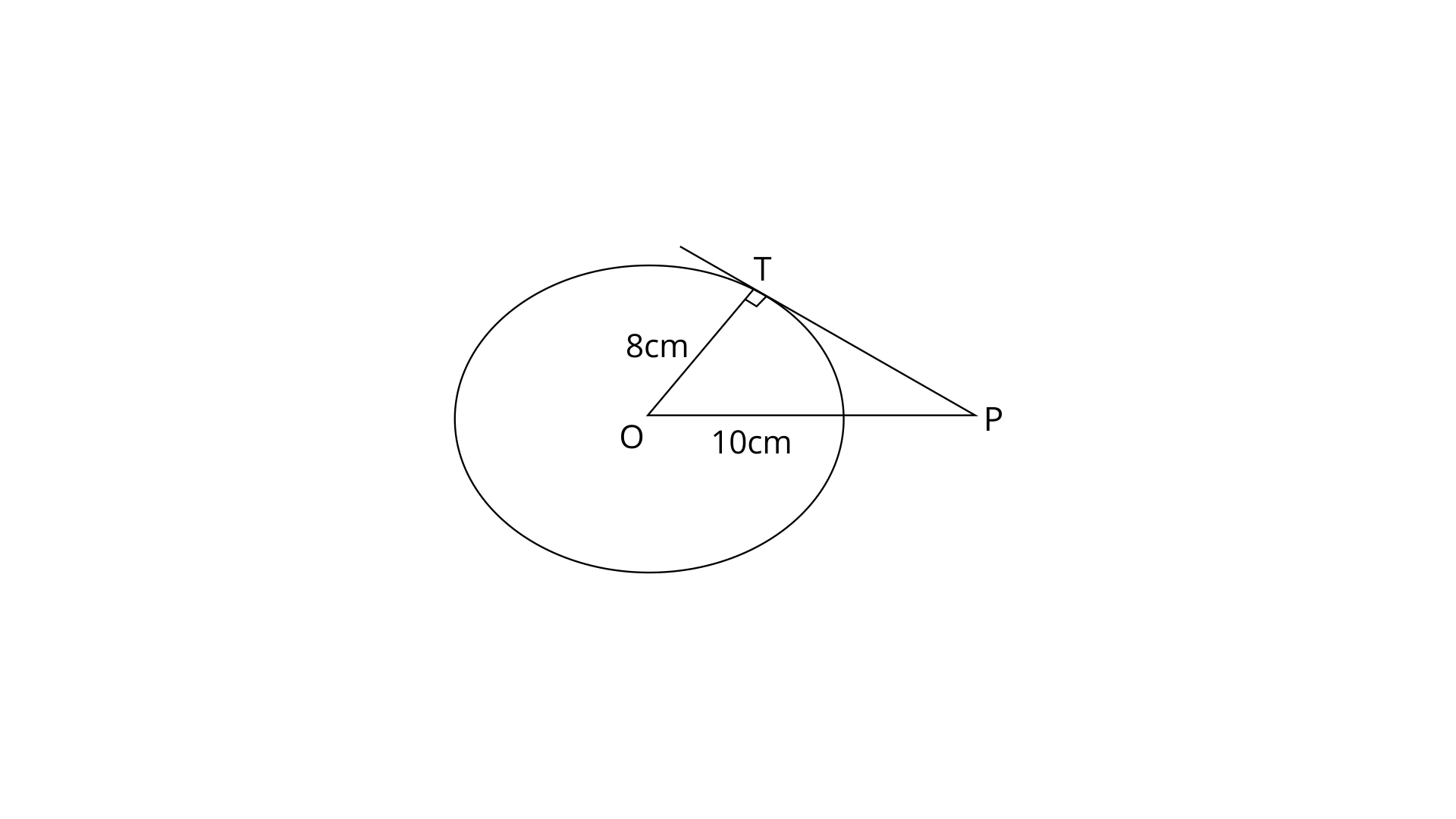
Given, Radius OT=8cm
OP=10cm
Radius is perpendicular to the tangent on the circle. Therefore
Now by using the pythagoras theorem in
Thus the length of the tangent is 6cm.
2. In the given figure, O is the centre of the circle and AB is a tangent at B. If AB=15cm and AC=7.5cm, calculate the radius of the circle.
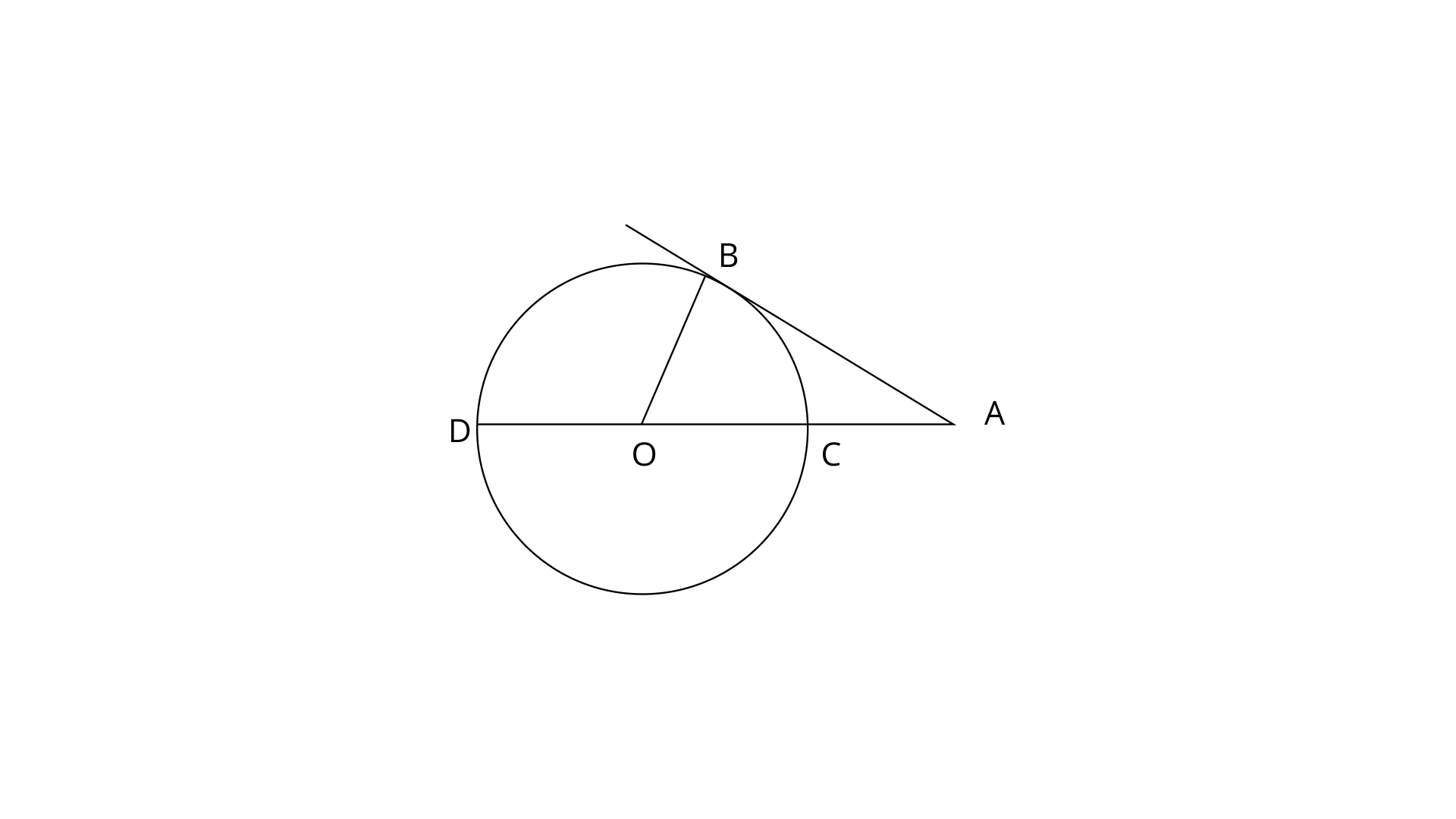
Ans:
Given, AB=15cm, AC=7.5cm
Let the radius of the circle is r.
OB=OC=r
Radius is perpendicular to the tangent, therefore
Now by using pythagoras theorem in
Therefore the radius of circle is
3. Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
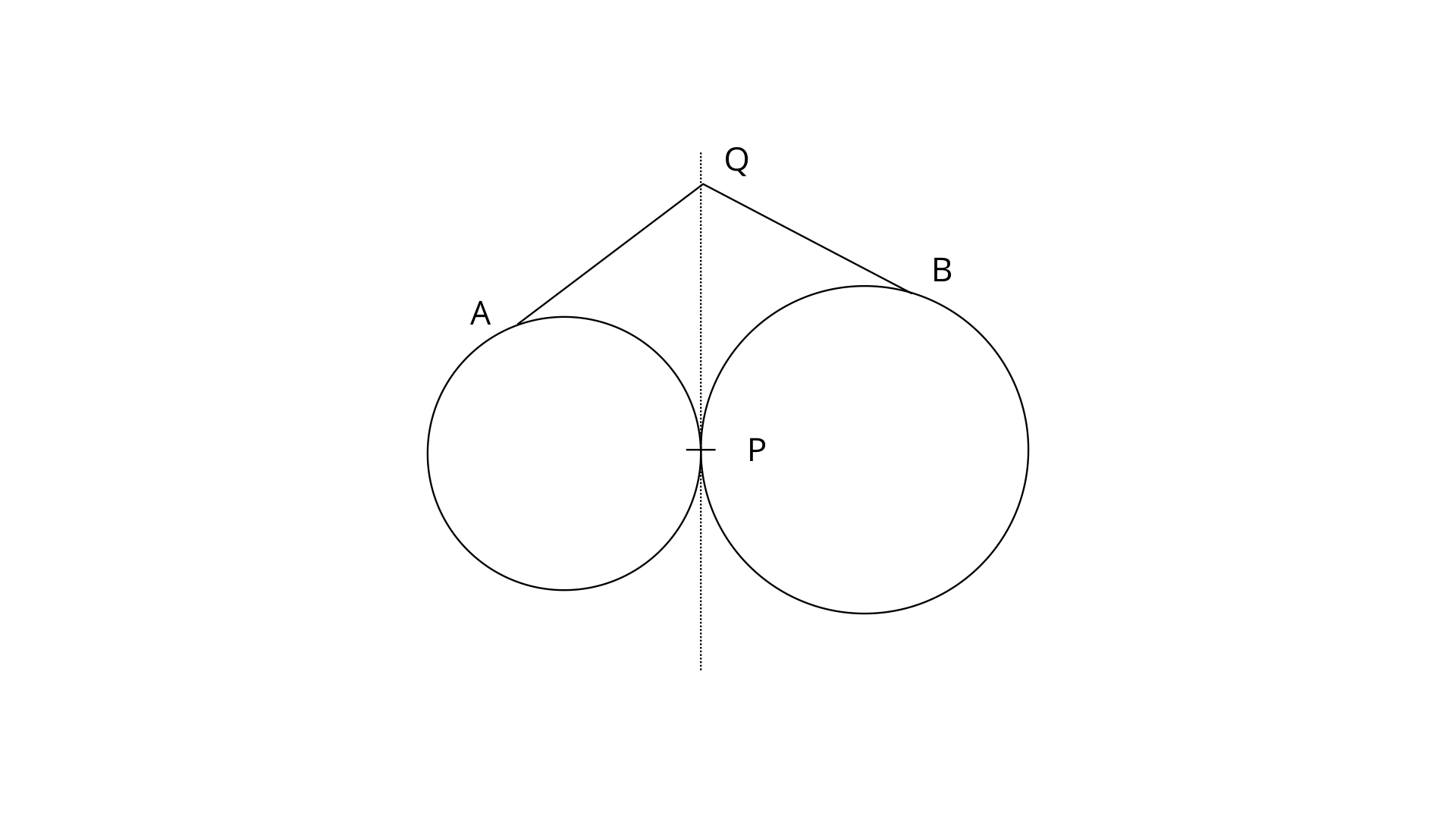
Ans: Tangents to circle from an exterior point are equal.
So, AQ=PQ------(1)
Again, BQ=PQ-----------(2)
From eq.(1) and (2)
AQ=BQ. (Hence proved)
4. Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
Ans:
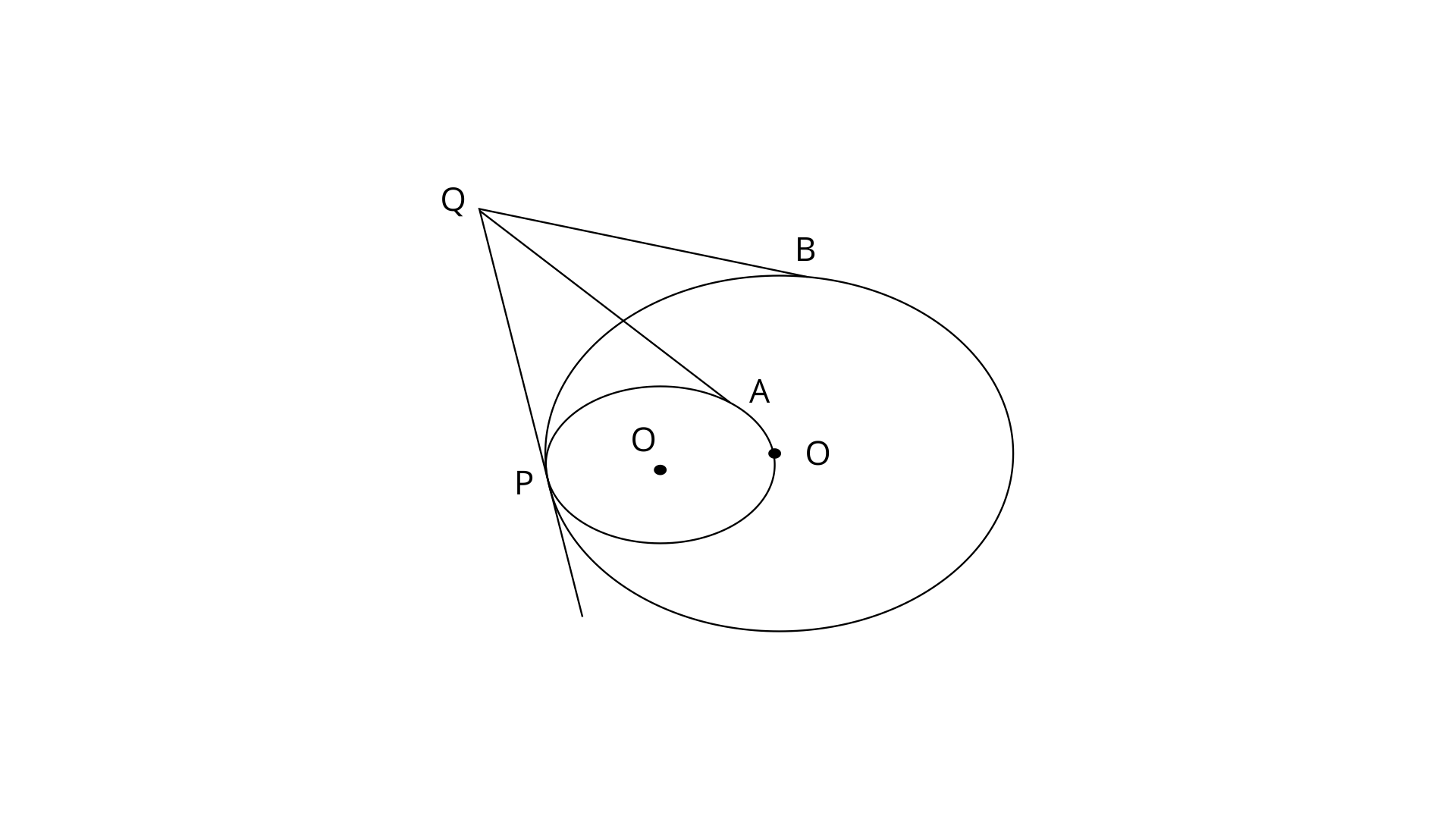
Tangents to a circle from an exterior point are equal.
Here PQ and QA are two tangents to the smaller circle from point exterior point Q.
Now, PQ and QB are two tangents to the large circle from point Q.
From eq. (1) and (2)
Hence proved.
5. Two circles of radii 5cm and 3cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Ans:
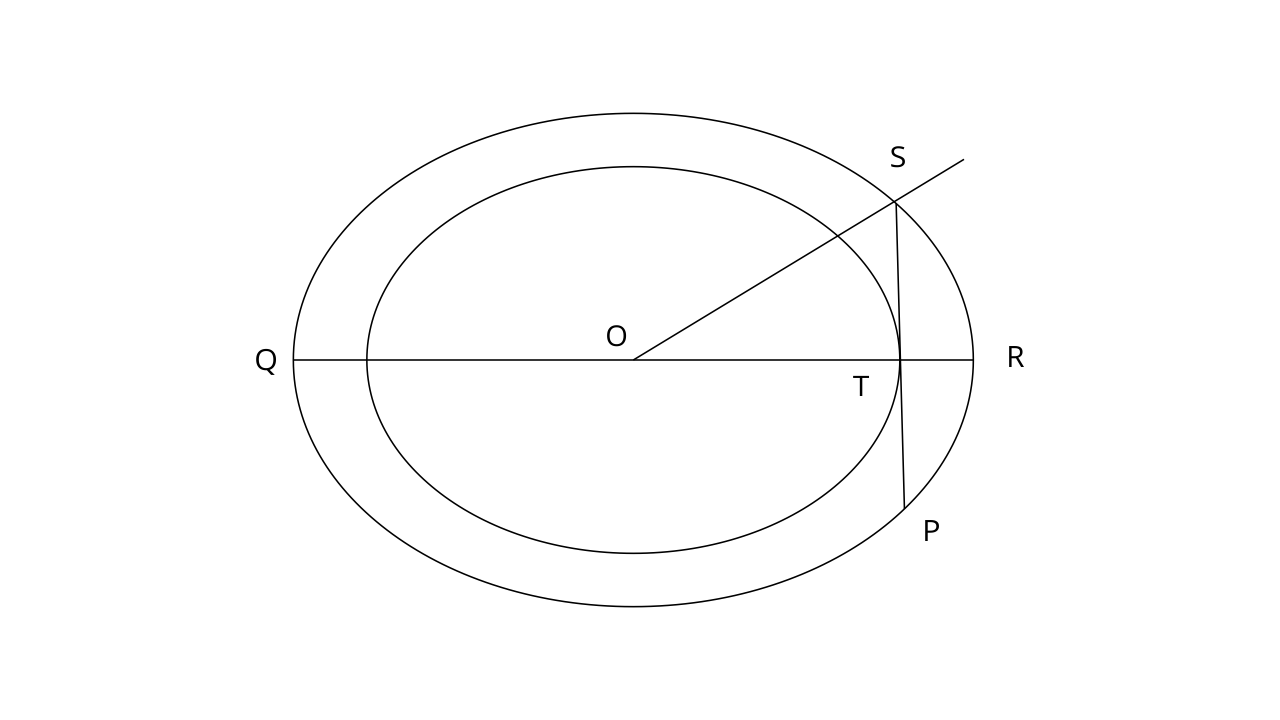
The radii of the concentric circles are 5cm and 3cm.
Sinc, SP is the chord of the larger circle and tangent to the smaller circle as well. OT is the radius of the smaller circle and we know that radius is perpendicular to the tangent. Therefore, OST is a right angle triangle.
By using pythagoras theorem in
OT is perpendicular to the chord SP, Hence SP bisects the SP.
Therefore,
Thus the length of the chord SP is 8cm.
6. Three circles touch each other externally. A triangle is formed when the centres of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6cm, 8cm and 9cm.
Ans:
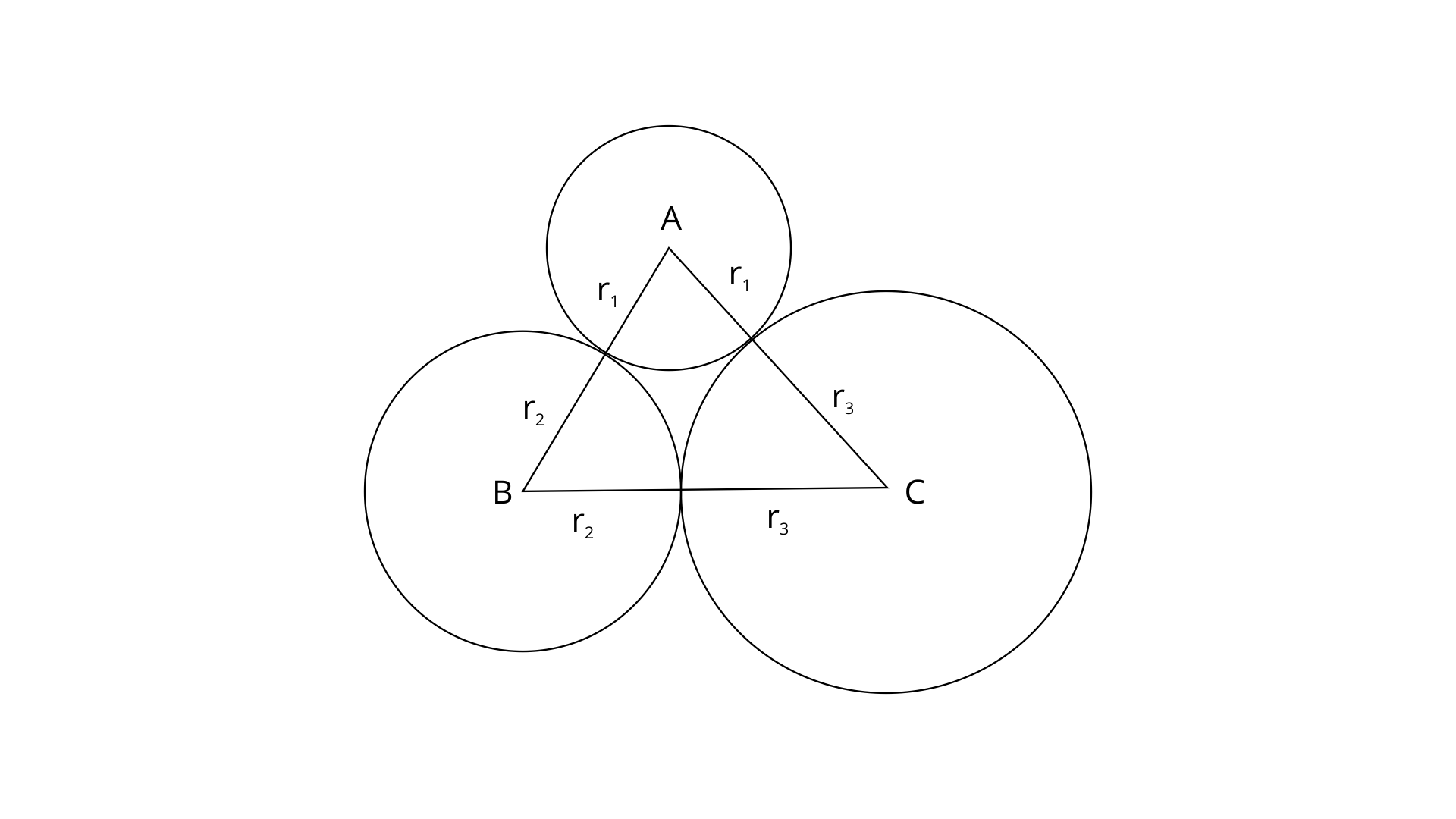
Let the radii of the circles are
Given, The sides of the triangle are 6cm, 8cm, 9cm.
From the diagram,
Adding eq.(1), (2) and (3)
Substituting
Now, substituting
Therefore, the radii of circles are 2.5cm, 3.5cm, 5.5cm.
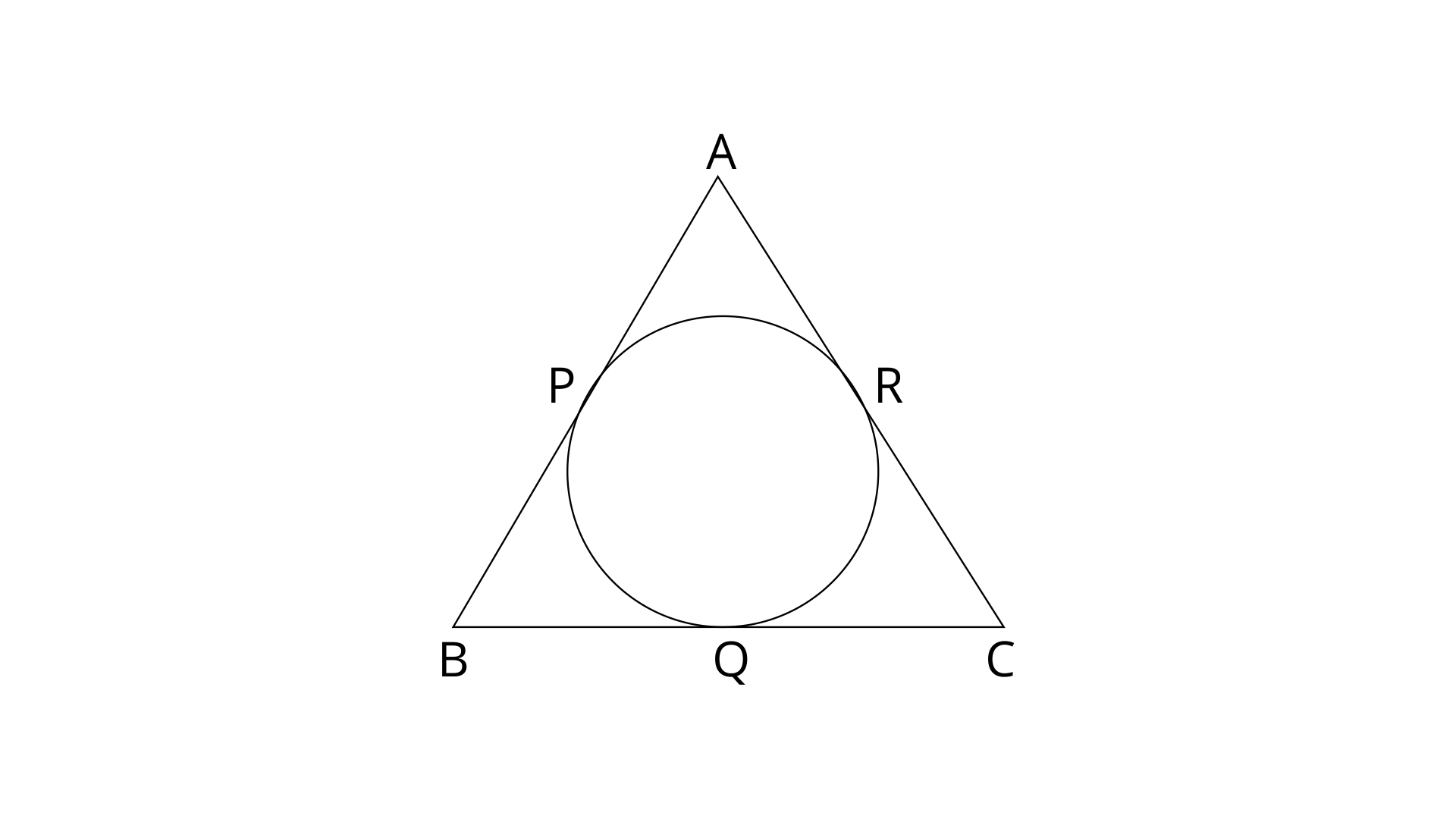
7. If the sides of a quadrilateral ABCD touch a circle, prove that:
AB+CD=BC+AD.
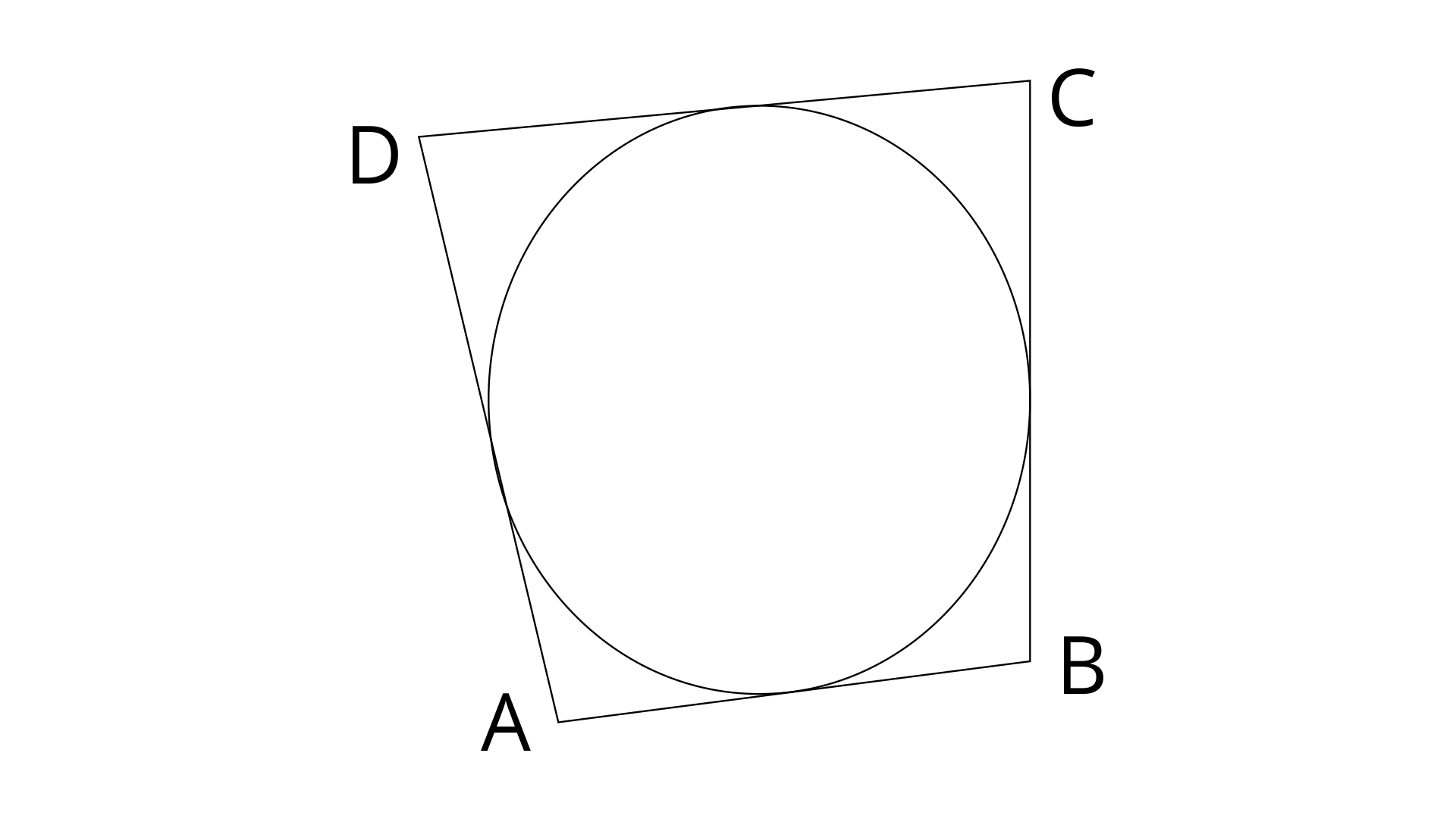
Ans:
Let the points P,Q,R and S are the points on sides AB, BC, CD and AD respectively.
Tangents to the circle from an exterior angle are equal.
Since AP and AS are the tangents to the circle from external point A.
AP=AS-----------(1)
Similarly,
BP=BQ-----------(2)
CR=CQ----------(3)
DR=DS-----------(4)
Add equation (1),(2),(3) and (4)
[since, AP+BP=AB, CR+DR=CD and AS+DS=AD, BQ+QC=BC]
Hence proved.
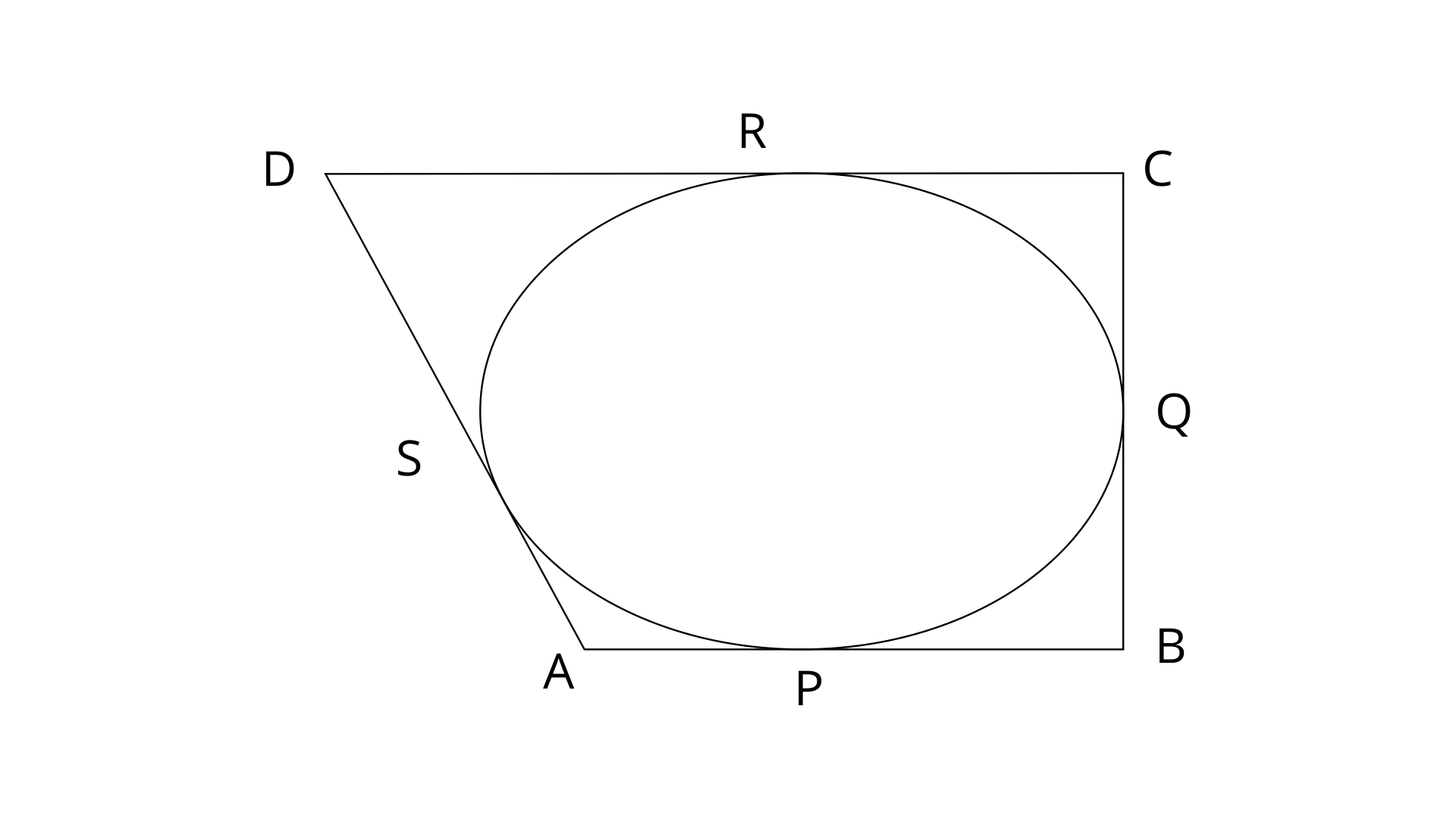
8. If the sides of a parallelogram touch a circle (refer figure of Q.7), prove that the parallelogram is a rhombus.
Ans:

Let P, Q, R and S are the points on the sides AB, BC, CD and AD respectively of the quadrilateral ABCD.
We know that the tangents to a circle from an external point are always equal.
Tangents from point A to the circle are AP and AS.
So, AP=AS -------------(1)
Similarly, BP=BQ ----------(2)
CR=CQ -----------(3)
DR=DS -----------(4)
On adding eq. (1),(2),(3) and (4)
AP+BP+CR+DR=AS+BQ+CQ+DS
(AP+BP)+(CR+DR)=(AS+DS)+(BQ+CQ)
[Since, (AP+BP)=AB, (CR+DR)=CD and (AS+DS)=AD, BQ+CQ=BC]
Since ABCD is a parallelogram. Therefore AD=BC and AB=CD
Now,
Therefore,
Thus the parallelogram ABCD is a rhombus.
9. From the given figure, prove that:
AP+BQ+CR=BP+CQ+AR. Also, Show that:
AP+BQ+CR=
Ans: Tangents drawn to a circle from an exterior point are always equal.
AP and AR are drawn to the circle from exterior point A.
Hence, AP=AR -----------(1)
Similarly, BQ=BP --------(2)
And, CR=CQ -------------(3)
On adding eq. (1), (2) and (3)
On adding AP+BQ+CR both sides
Perimeter of a triangle is the sum of all the sides.
Therefore,
10. In the given figure of Q.9; if AB=AC then prove that: BQ=CQ.
Ans:

Tangents to a circle from an exterior point are always equal.
Here, AP and AR the tangents to the circle from the point A.
Hence, AP=AR ---------(1)
Similarly, BP=BQ -----------(2) and CQ=CR ----------(3)
On adding eq.(1), (2) and (3)
Given,
Therefore,
11. Radii of two circles are 6.3cm and 3.6cm. State the distance between their centres if :
(i). They touch each other externally.
(ii). They touch each other internally.
Ans:
(i).
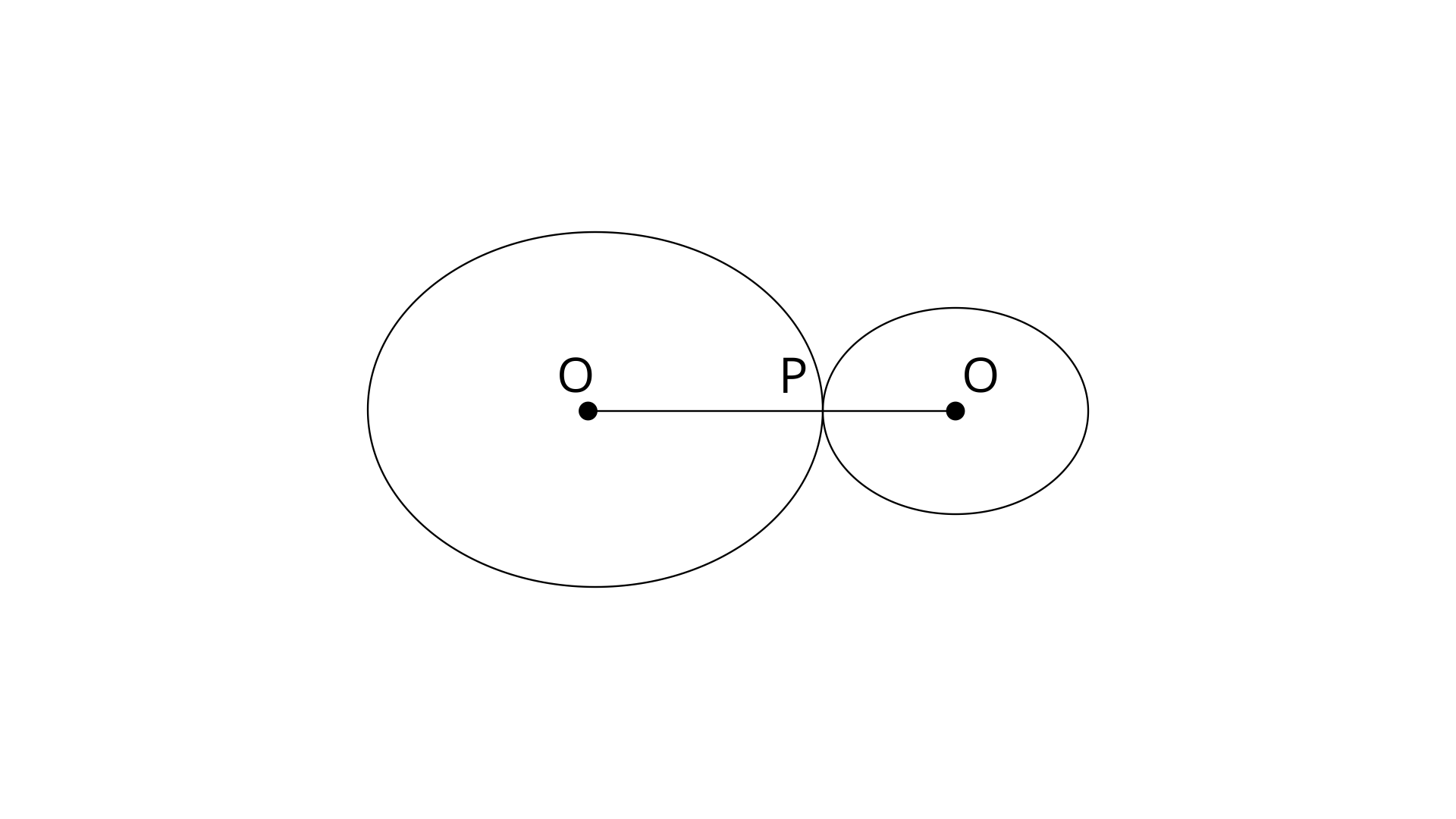
Let the centres of the circle be O,O’ and P is the touching points of the circles.
Radii of the circles are 6.3cm and 3.6cm.
Now the distance between centres is OO’=OP+O’P
=6.3cm+3.6cm=9.9cm
(ii).
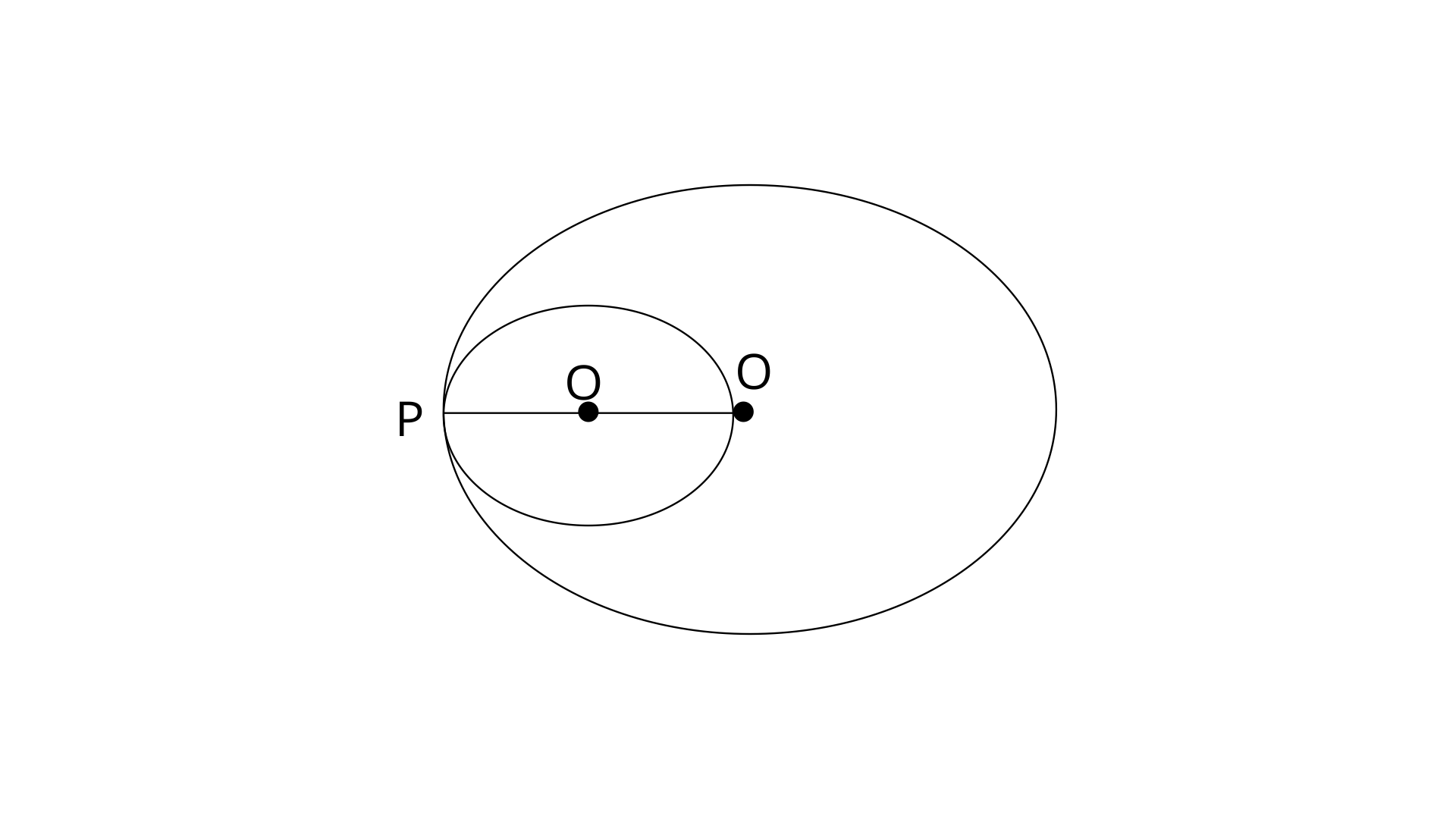
Radii of the circles are 6.3cm and 3.6cm. OP=6.3cm and O’P=3.6cm
Now the distance between centres is OO’=OP-O’P=6.3-3.6=2.7cm
12. From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that :
(i).
Ans:
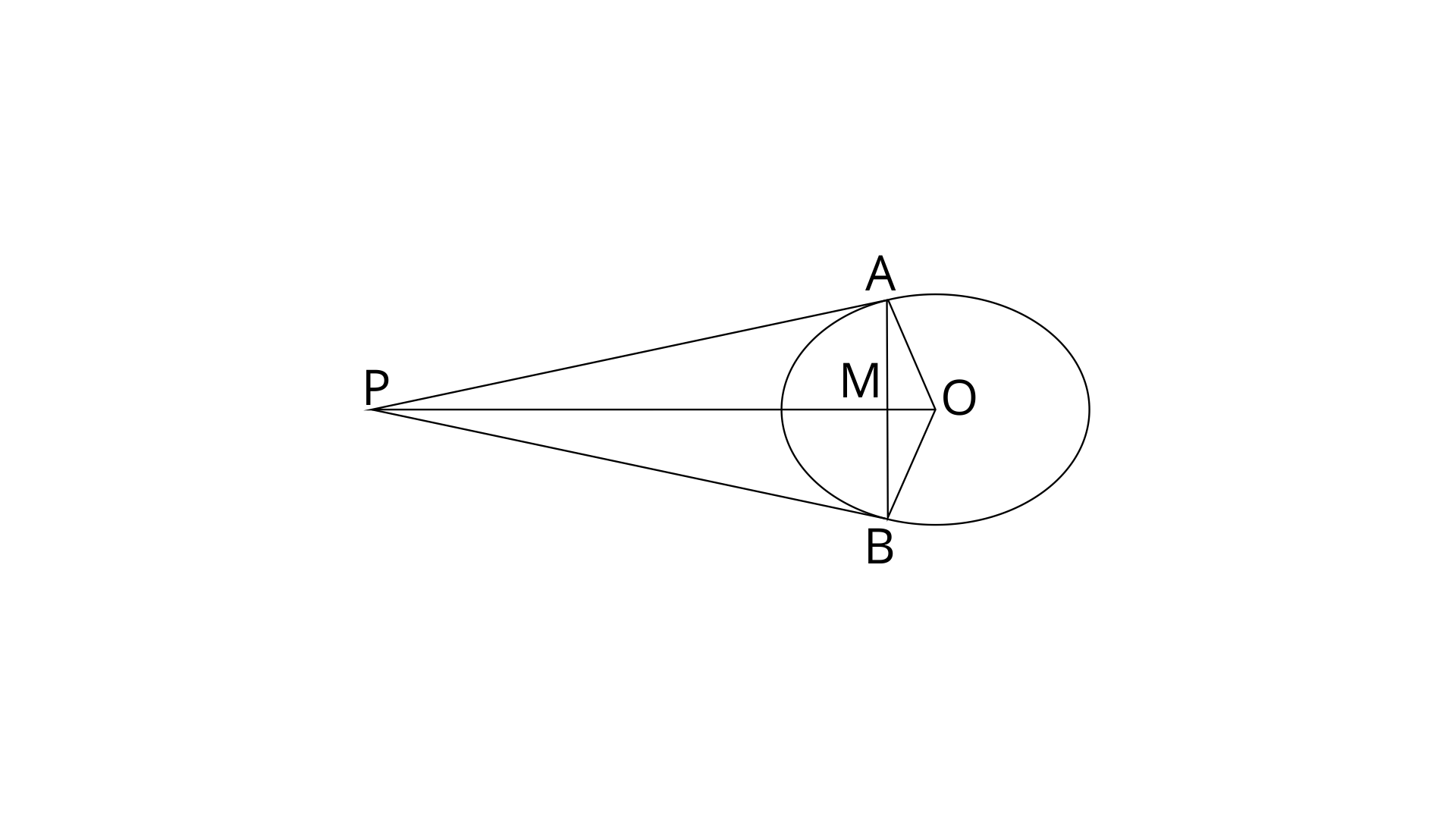
In
AP=BP (Tangents from an external points are equal)
OP=OP (common sides)
OA=OB (Radii of circle)
Therefore,
(ii). OP is the 丄 bisector of chord AB.
Ans: In
OM=OM (common sides)
OA=OB (Radii of same circle)
Therefore, AM=MB,
Since,
Thus OM and OP are perpendicular bisectors of chord AB.
13. In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
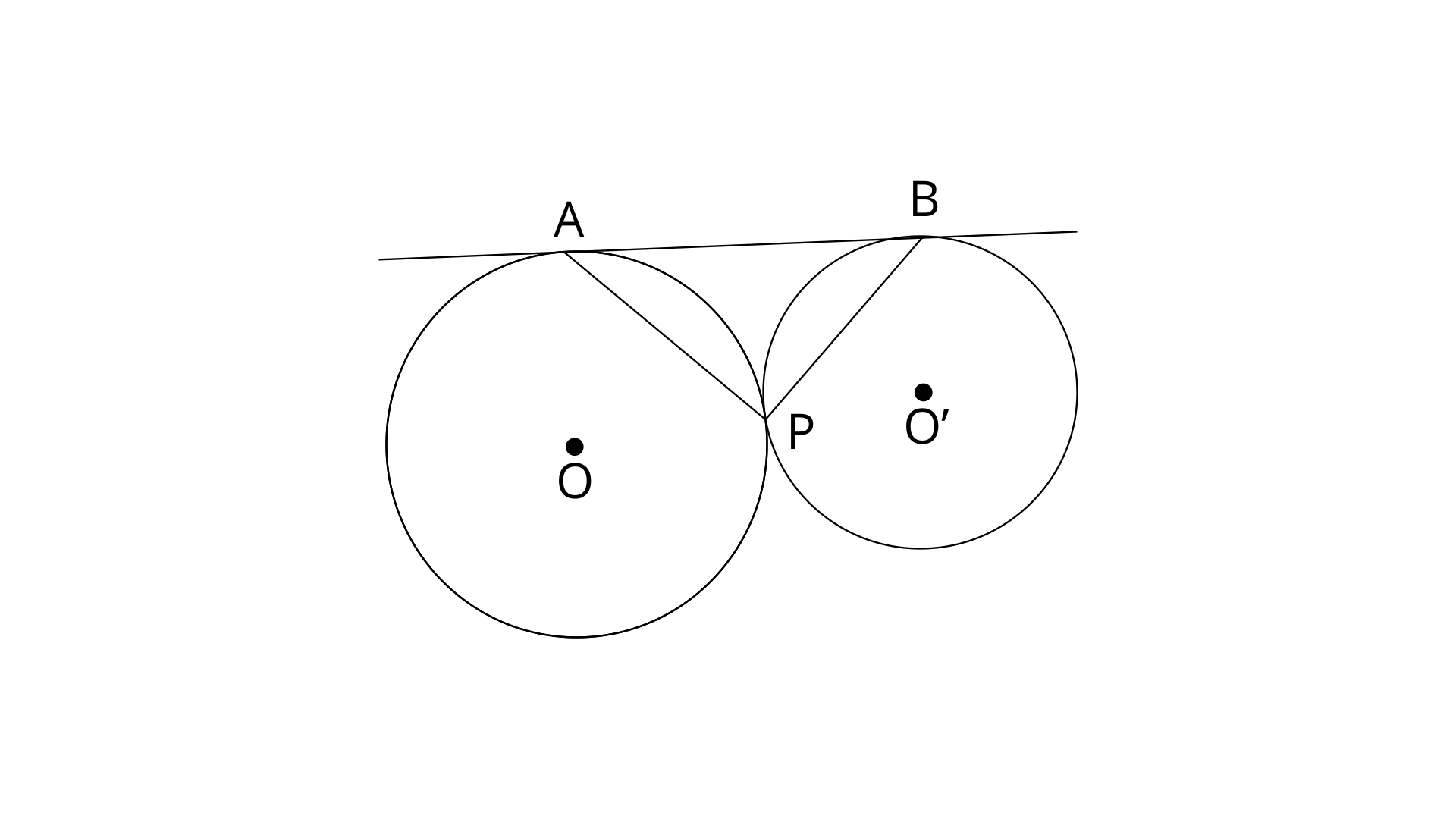
(i). Tangent at point P bisects AB,
Ans:
Let the common tangent touching both circles is TPT’
Tangents to a circle from an external point are equal. Here TP and TA are tangents to the circle from point T.
TA=TP ---------(1)
Similarly, AB=TB --------(2)
From eq.(1) and (2)
TA=TB=TP
Therefore TPT’ is a bisector of AB.
(ii). Angle
Ans: In
Since, TA=TB
Similarly,
TP=TB
On adding from eq. (1) and (2)
In
14. Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that :
Ans:
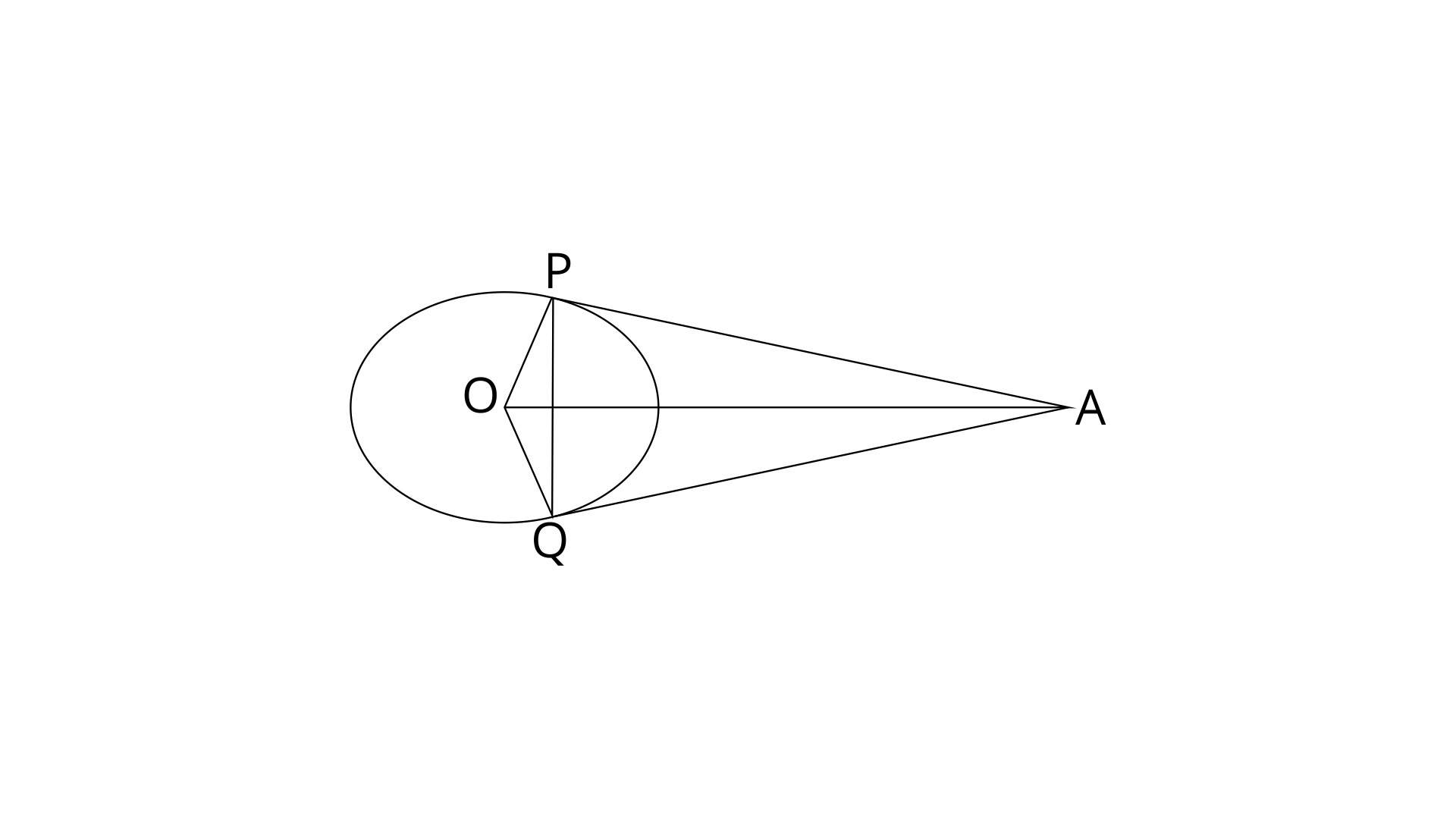
Radius is perpendicular to the tangent.
Therefore,
OPAQ is a quadrilateral and the sum of all the angles in a quadrilateral is
In
OP=OQ (Radii of same circle)
Using angle sum property,
From eq. (1) and (2)
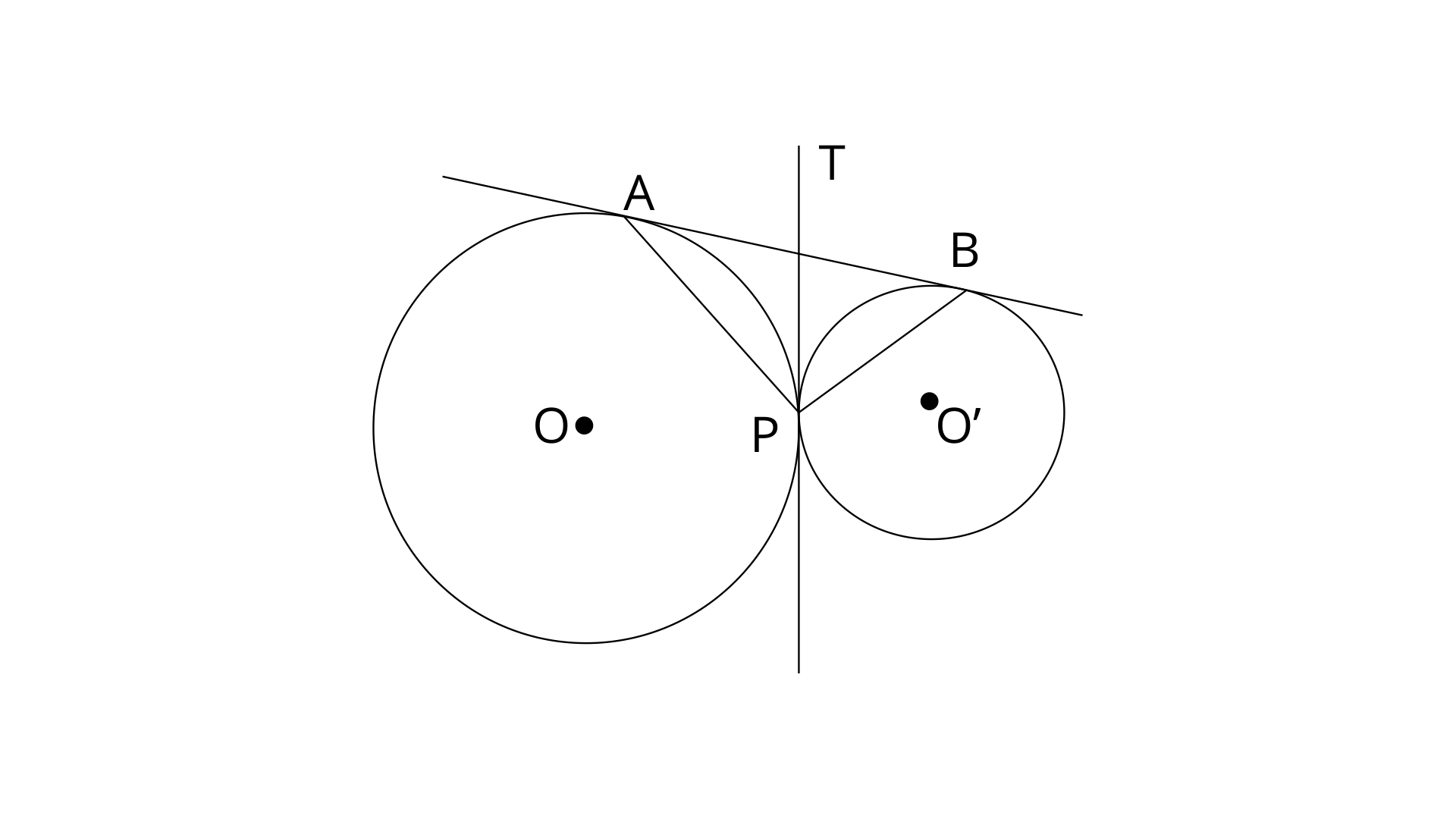
15. Two parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right at the centre.
Ans:
Join points OP, OQ and OC.
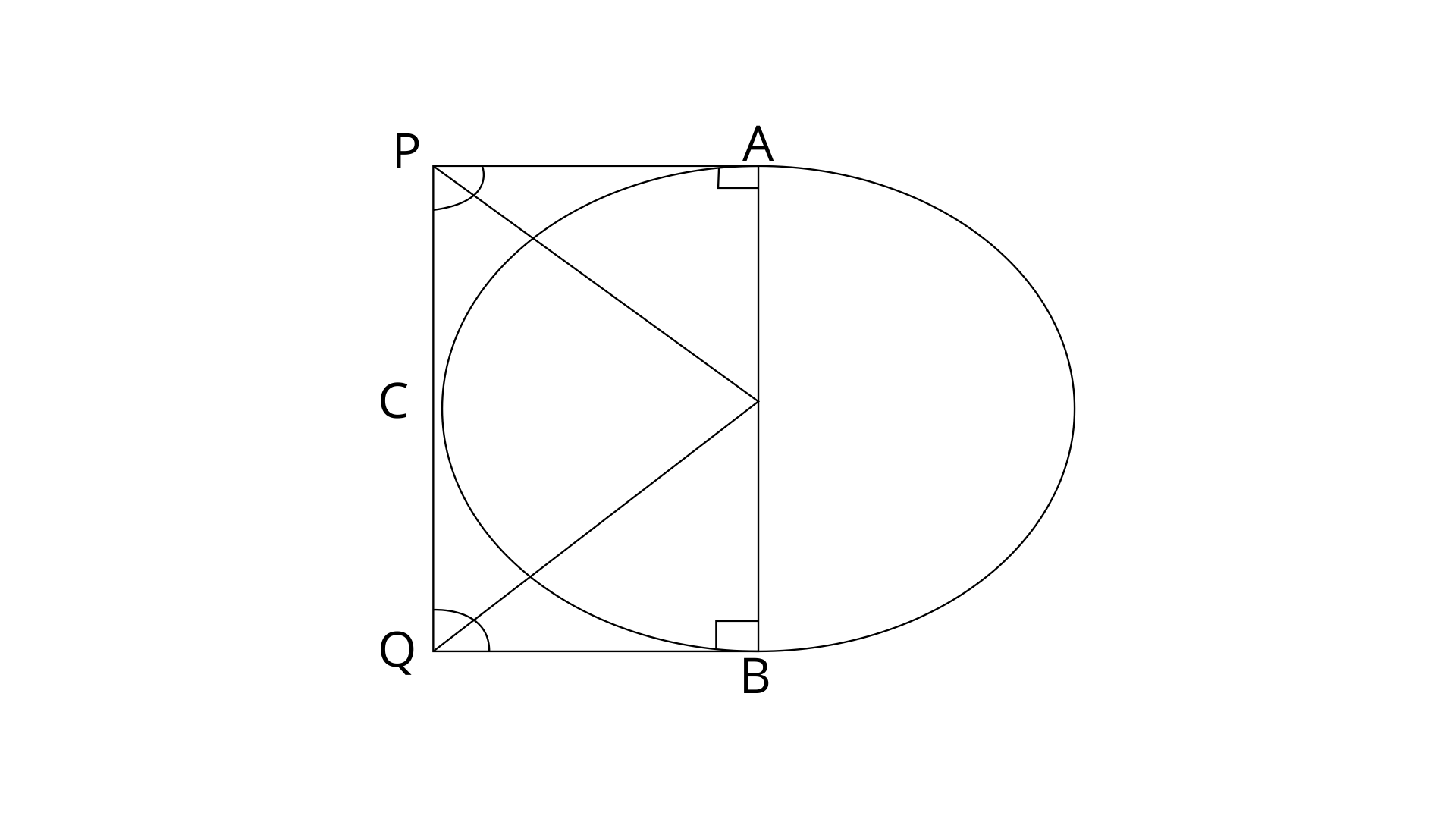
In
OP=OP (Common side)
OA=OC (Radii of same circle)
PA=PC ( Tangents to the circle from external point)
Therefore,
Similarly,
Therefore,
Since, AP||BQ
Now in
Thus PQ subtends the right angle at centre.
16. ABC is a right angled triangle with AB=12cm and AC=13cm. A circle, with centre O, has been inscribed inside the triangle.
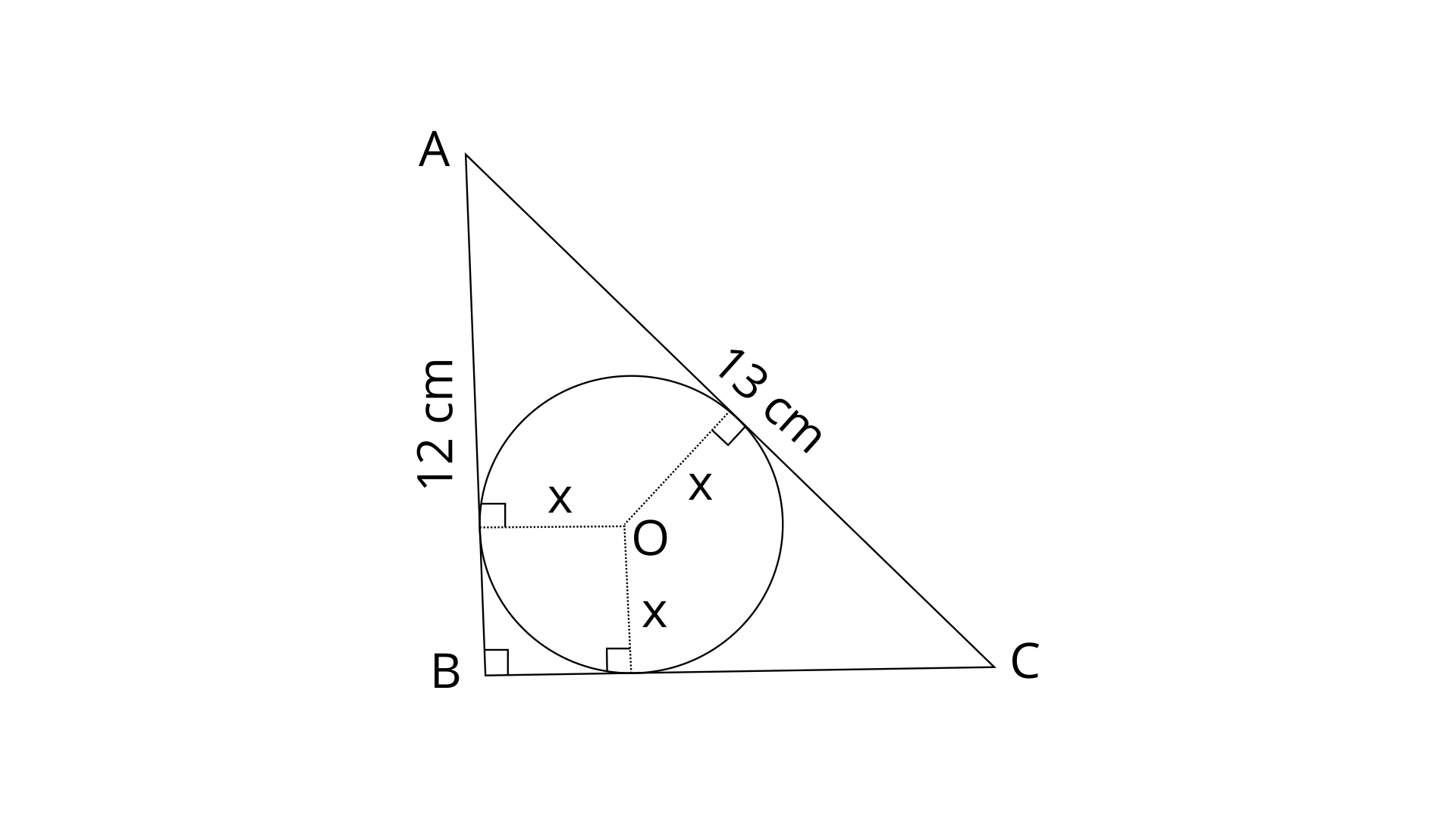
Calculate the value of x, the radius of the inscribed circle.
Ans:
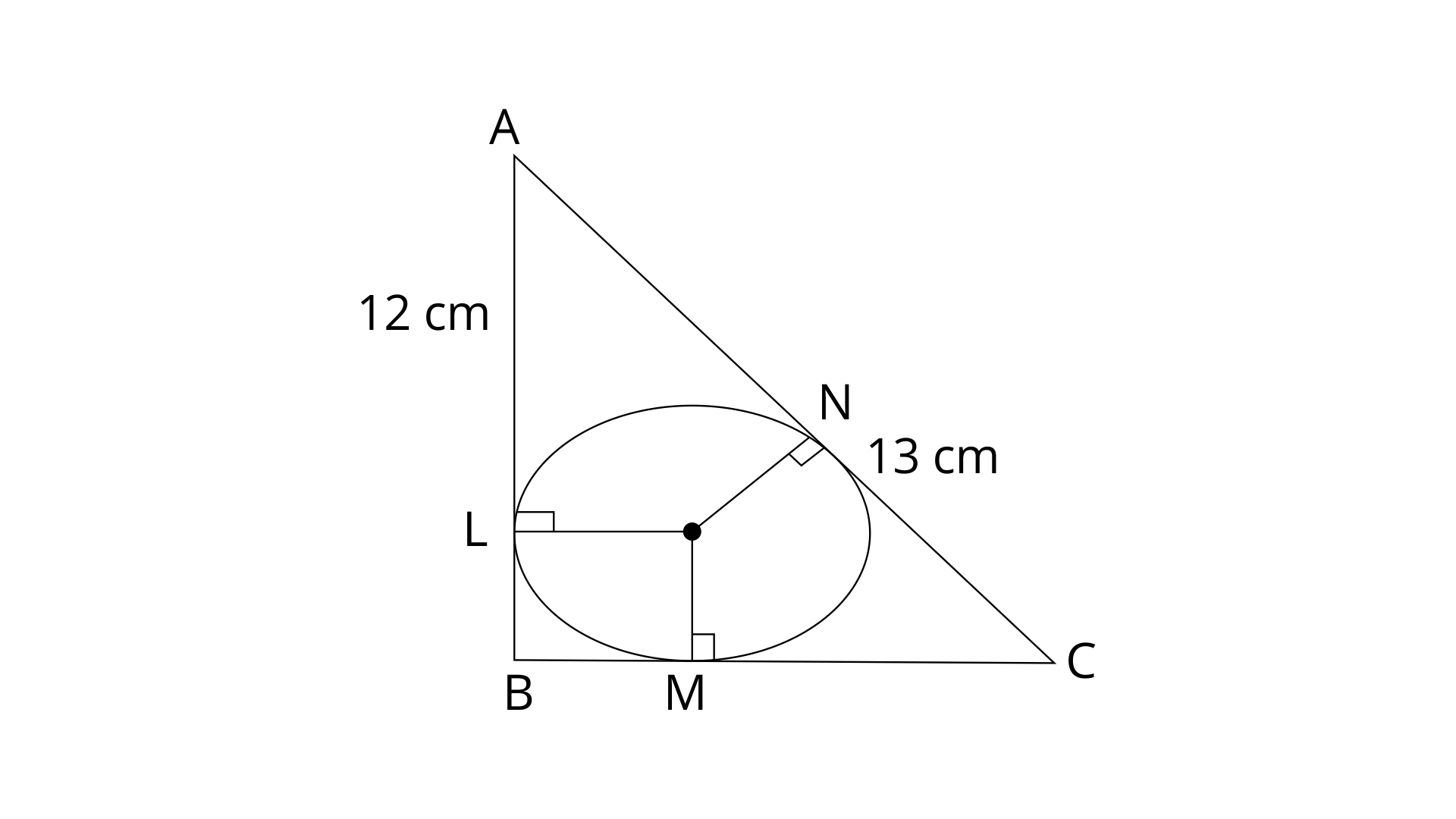
Let the altitude points are L, M and N on sides AB, BC and AC respectively.
In
LBMO is a square.
LB=MB=MO=OL=LN=x.
AL=12-LB=12-x.
Tangents to a circle from an exterior point are equal.
AN=AL=12-x
Since, ABC is a right angle triangle. So by using pythagoras theorem
Now, MC=BC-BM=5-x.
Tangents to a circle from an exterior point are equal.
NC=MC=5-x
Since,
Thus the value of x is
17. In a triangle ABC, the incircle(centre O) touches the BC, CA and AB at points P,Q and R respectively. Calculate that :
(i).
(ii).
given that
Ans:
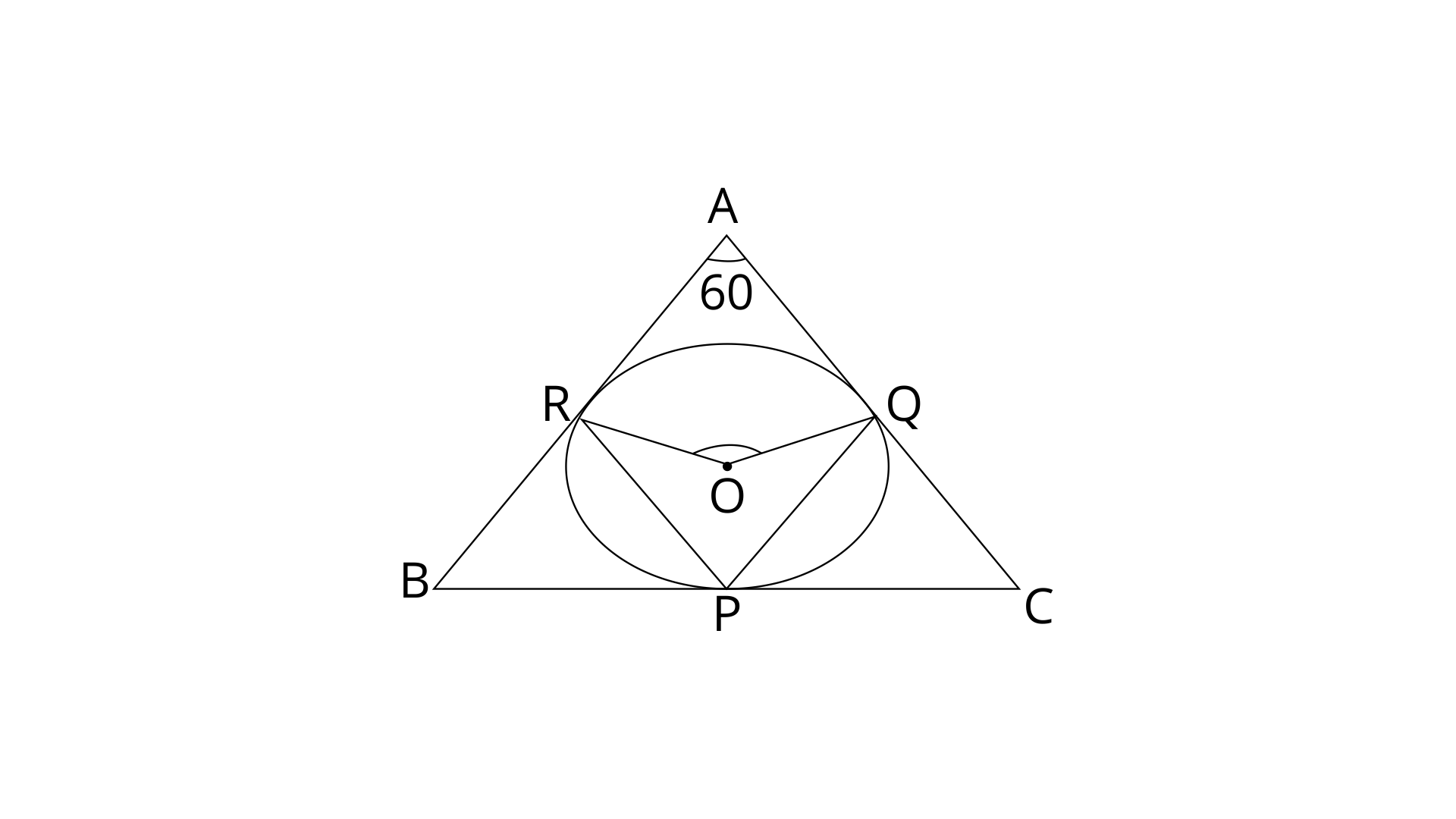
(i).
Ans: In triangle ABC, the circle touches AB, BC and AC at points R, P and Q respectively.
In quadrilateral AROQ the sum of all the angles is
Since OR, OQ are radii and AR, AQ are tangents to the circle from external point A. We know that the radius is perpendicular to the tangent.
Hence,
Thus the value of
(ii).
Ans: In a circle, the angle at the centre is doubled the angle at circumference subtended by the same chord.
Thus the value of angle
18. In the following figure, PQ and PR are tangents to the circle, with centre O. If
(i).
(ii).
(iii).
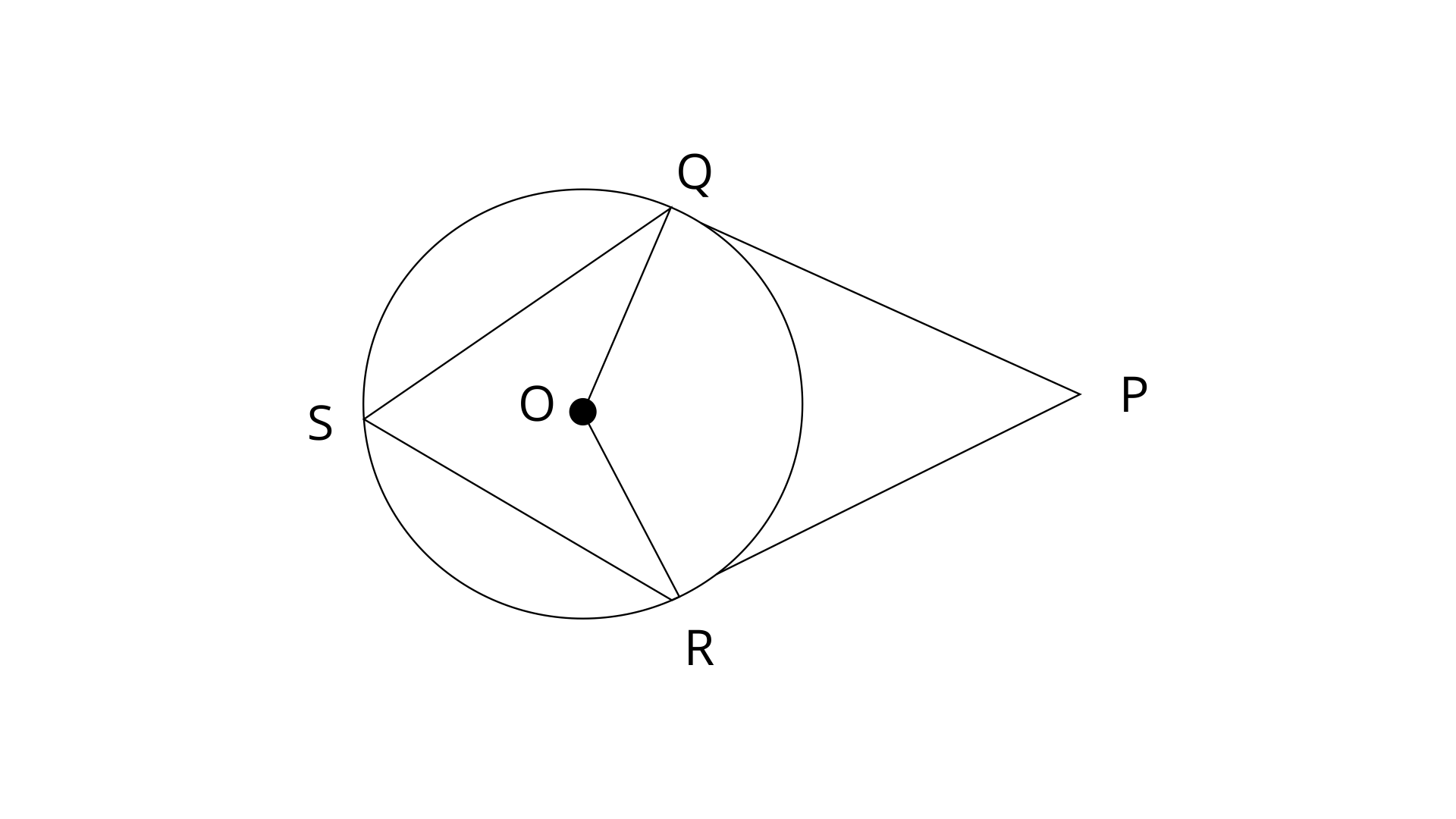
Ans: Join the points QR.
(i).
Ans: PQ and PR are the tangents to the circle from external point P.
Hence, PQ=PR
Tangent is perpendicular to the radius.
PQOR is a quadrilateral and in a quadrilateral the sum of angles in a quadrilateral is
Thus the value of
(ii).
Ans: In
OQ=OR (Radii of same circle)
Therefore,
Now, By using angle sum property,
Thus the value of
(iii).
Ans: In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
Thus the value of
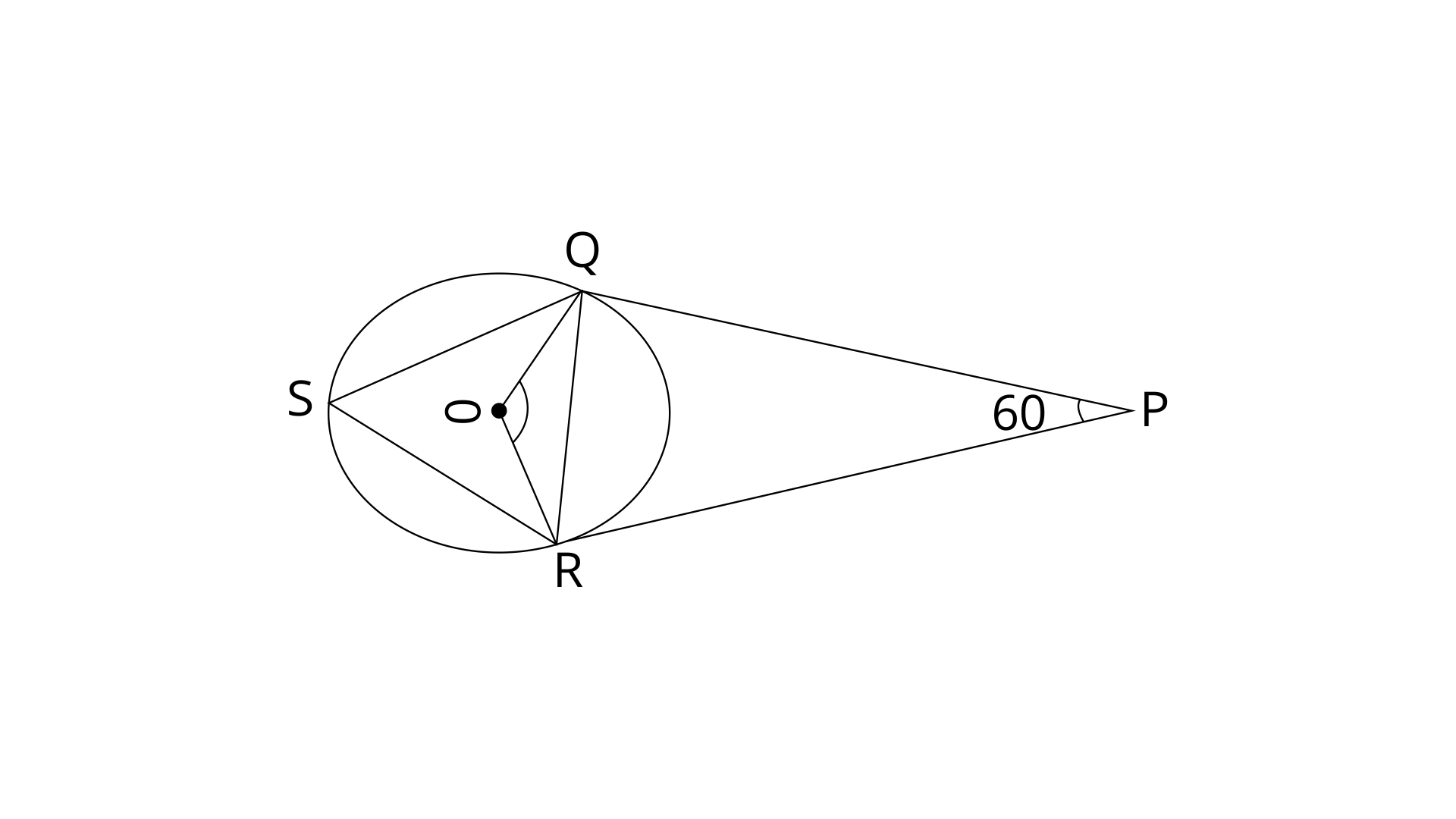
19. In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
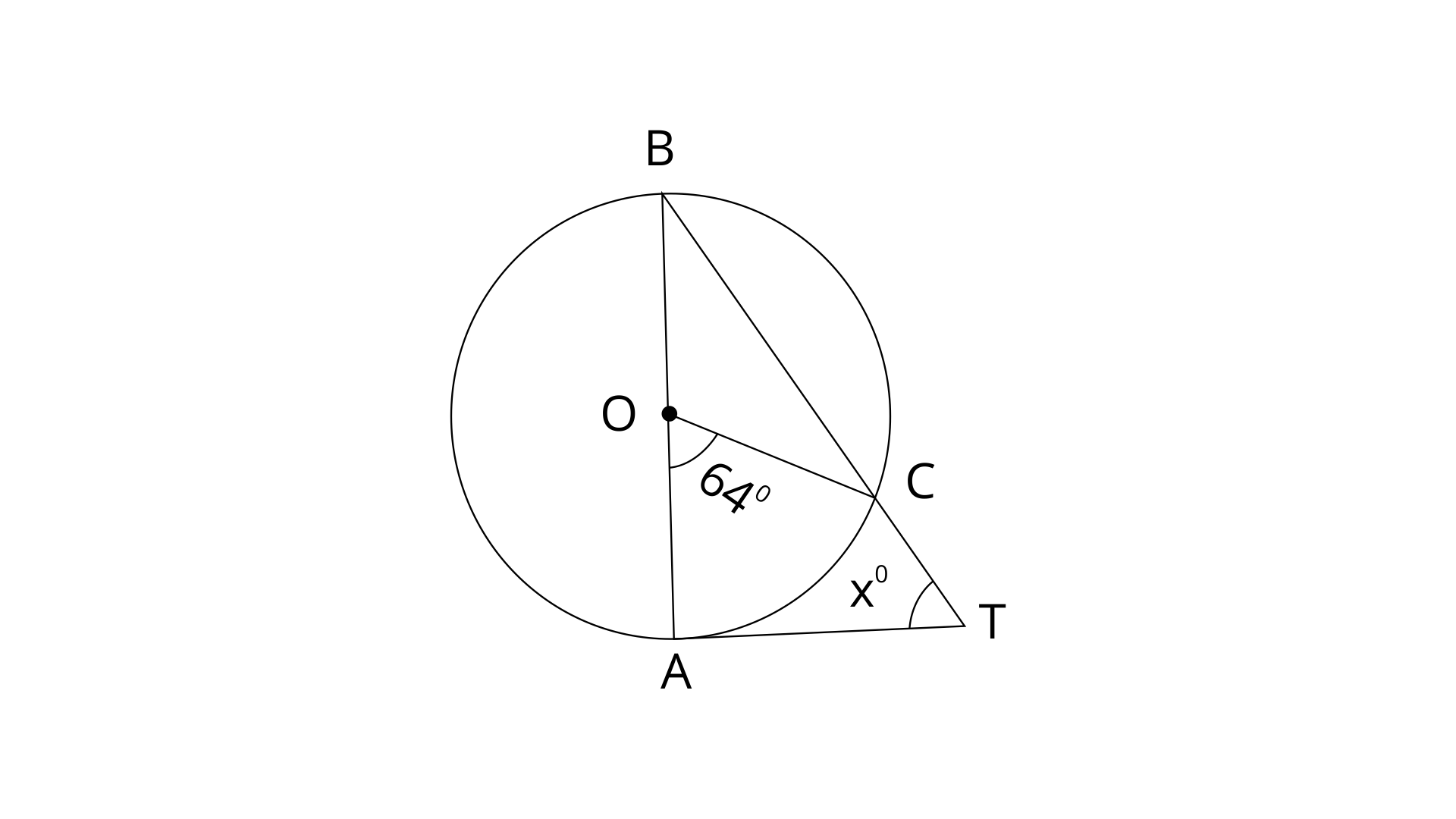
Ans:
In
OB=OC (Radii of same circle)
Exterior angle in a triangle is the sum of the opposite angles. Here angle
Now in
Since AT is tangent and AB is a diameter. We know that the radius is perpendicular to the tangent. Hence,
Thus the value of
20. In quadrilateral ABCD; angle
Ans:
In quadrilateral ABCD,
Tangents to a circle from an external point are equal. Here BQ and BR the tangents from the external points B.
Therefore, BQ=BR=27cm
∵BC=38cm
Since, Tangents CS and CR are tangents from external point C.
Therefore CS=CR=11cm.
Now, DS and DP are tangents to the circle from external point D.
Therefore, DP=DS=14cm
AD, DC are tangents and OP, OS are radius. Radius is perpendicular to the tangent.
Therefore the radius OS is 14cm.
21. In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given
Prove that:
(i).
(ii). Write an expression connecting x and y.
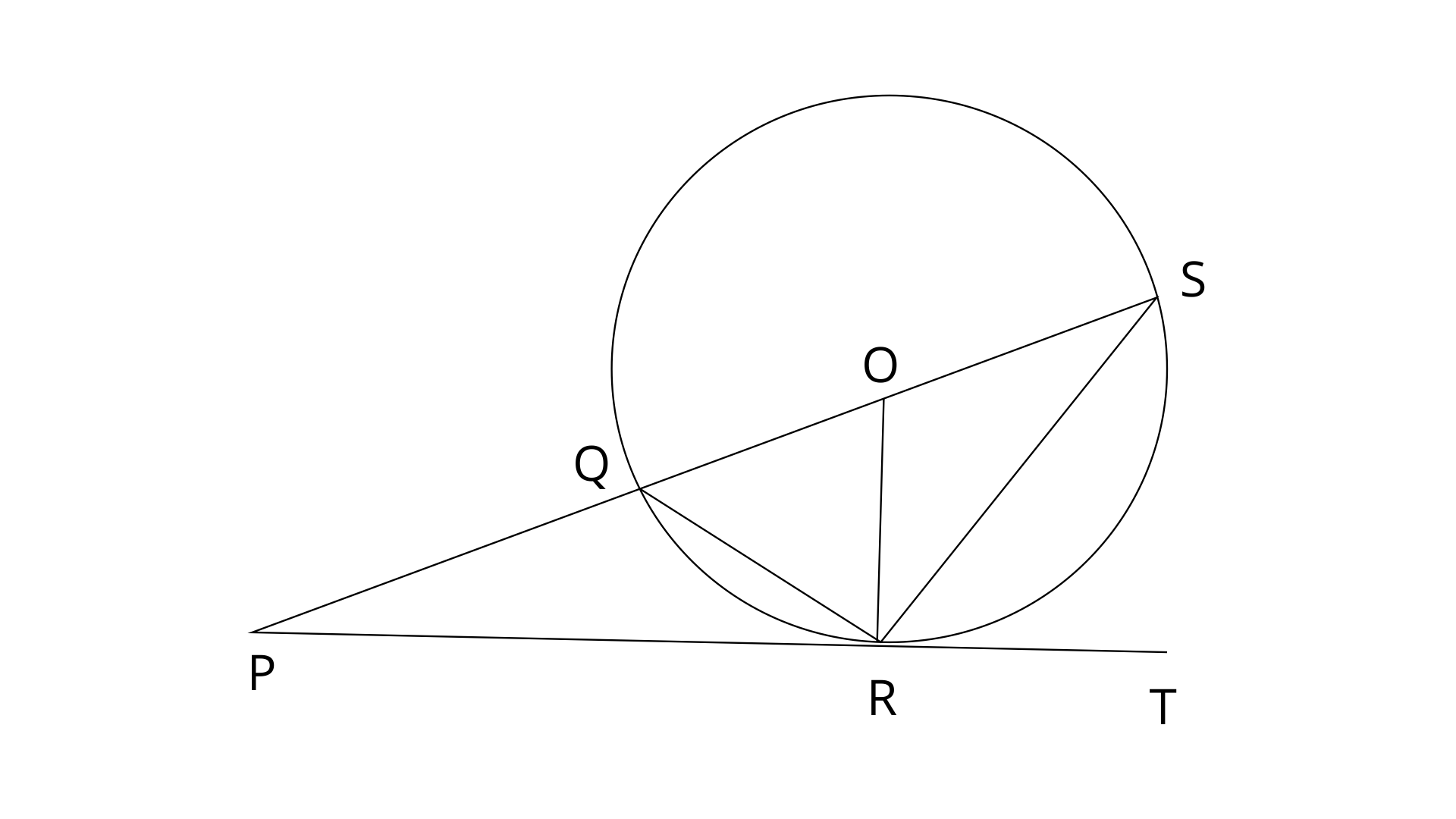
Ans:
Since PT is a tangent at point R and OR is the radius of the circle.
Hence,
Given,
Since,
Therefore,
Since, OS=OR (Radii of same circle)
(ii). Since, OR=OQ (Radii of same circle)
ext.
22. PT is a tangent to the circle at T. If
(i).
(ii).
(iii).
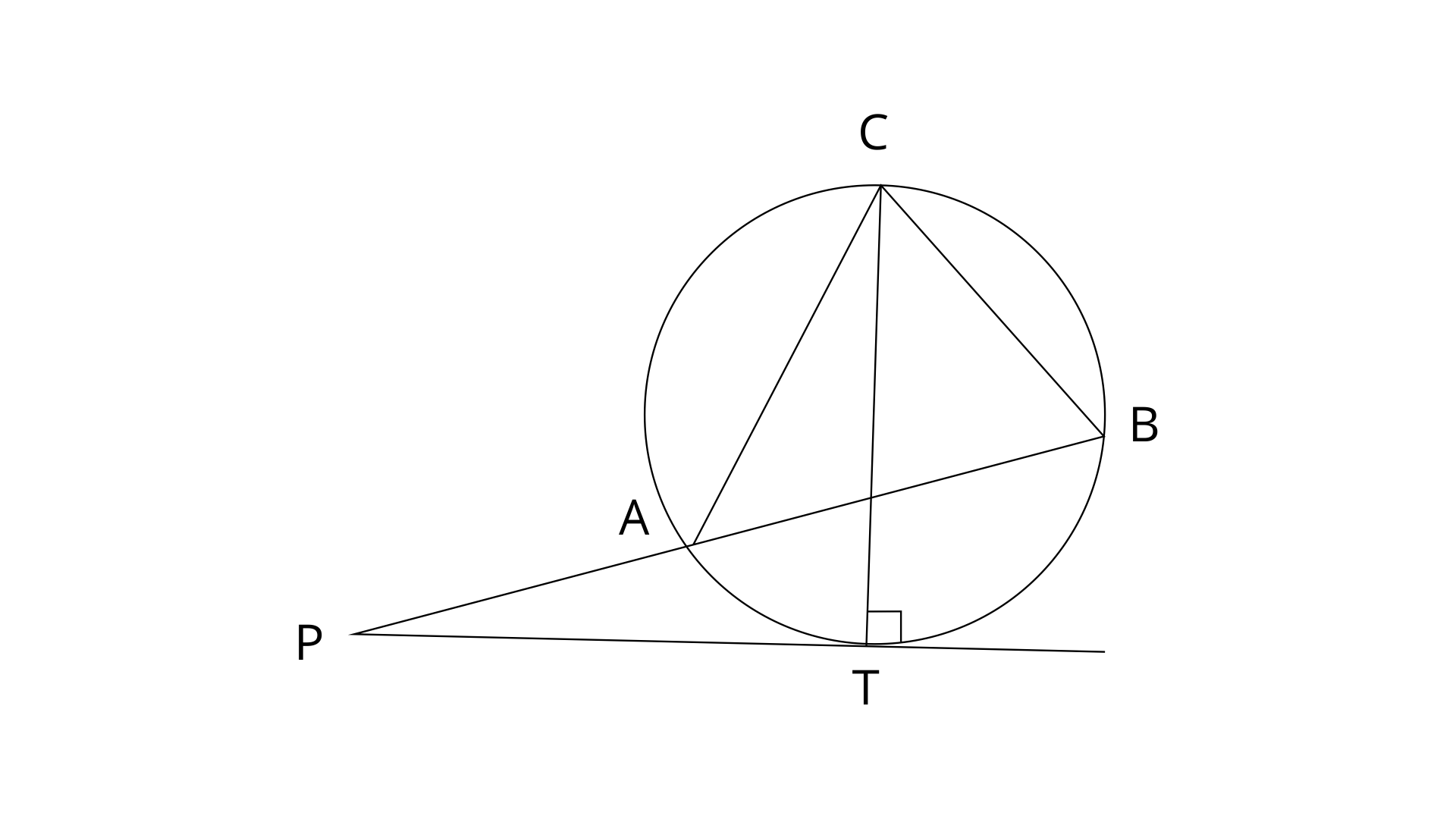
Ans: join the points AT, BT
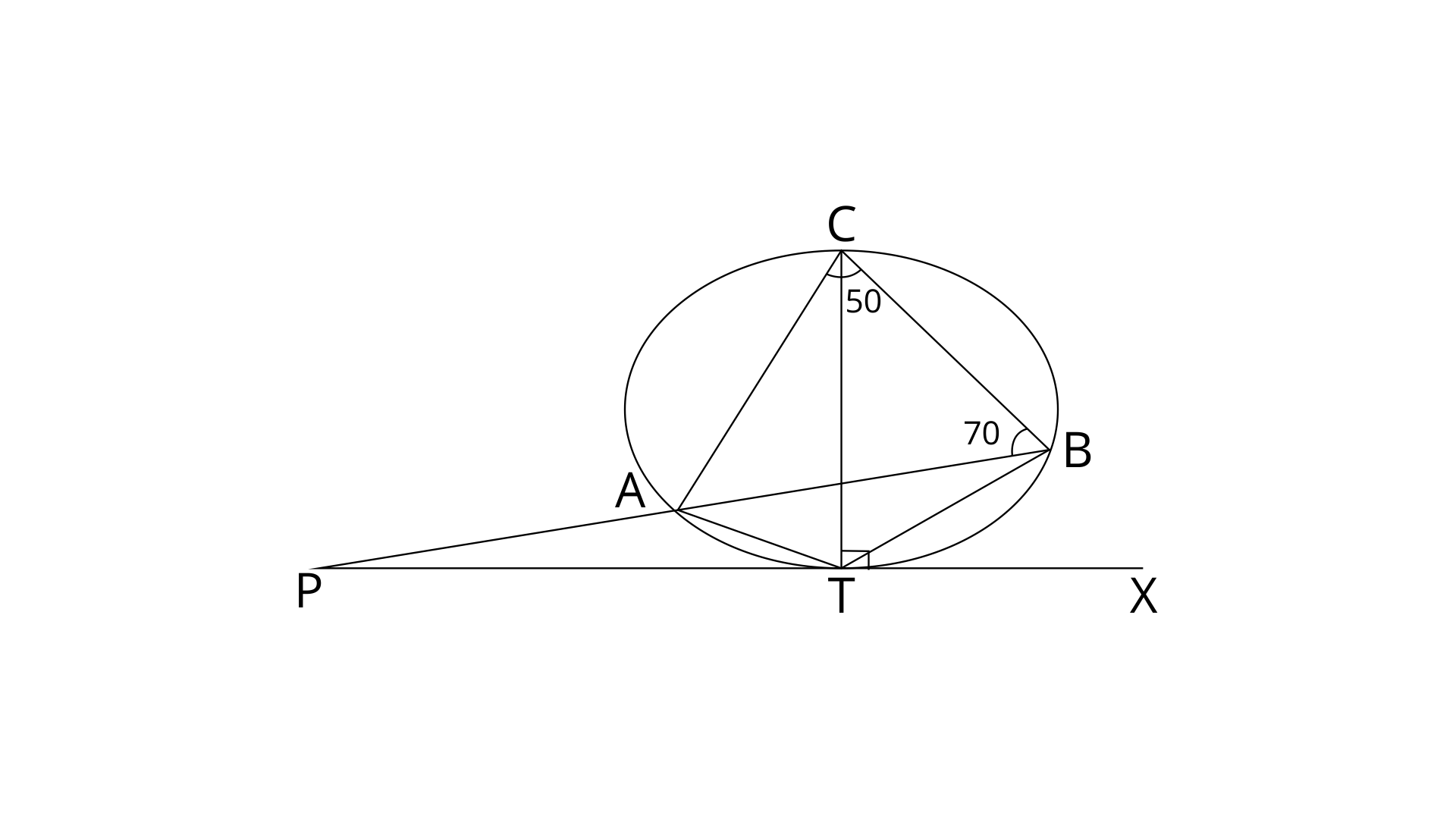
(i).
Ans: PX is a tangent to the circle at point T.
Angle
Hence,
(ii).
Ans: In
Hence,
(iii).
Ans: PT is tangent and AT is a chord,
23. In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle
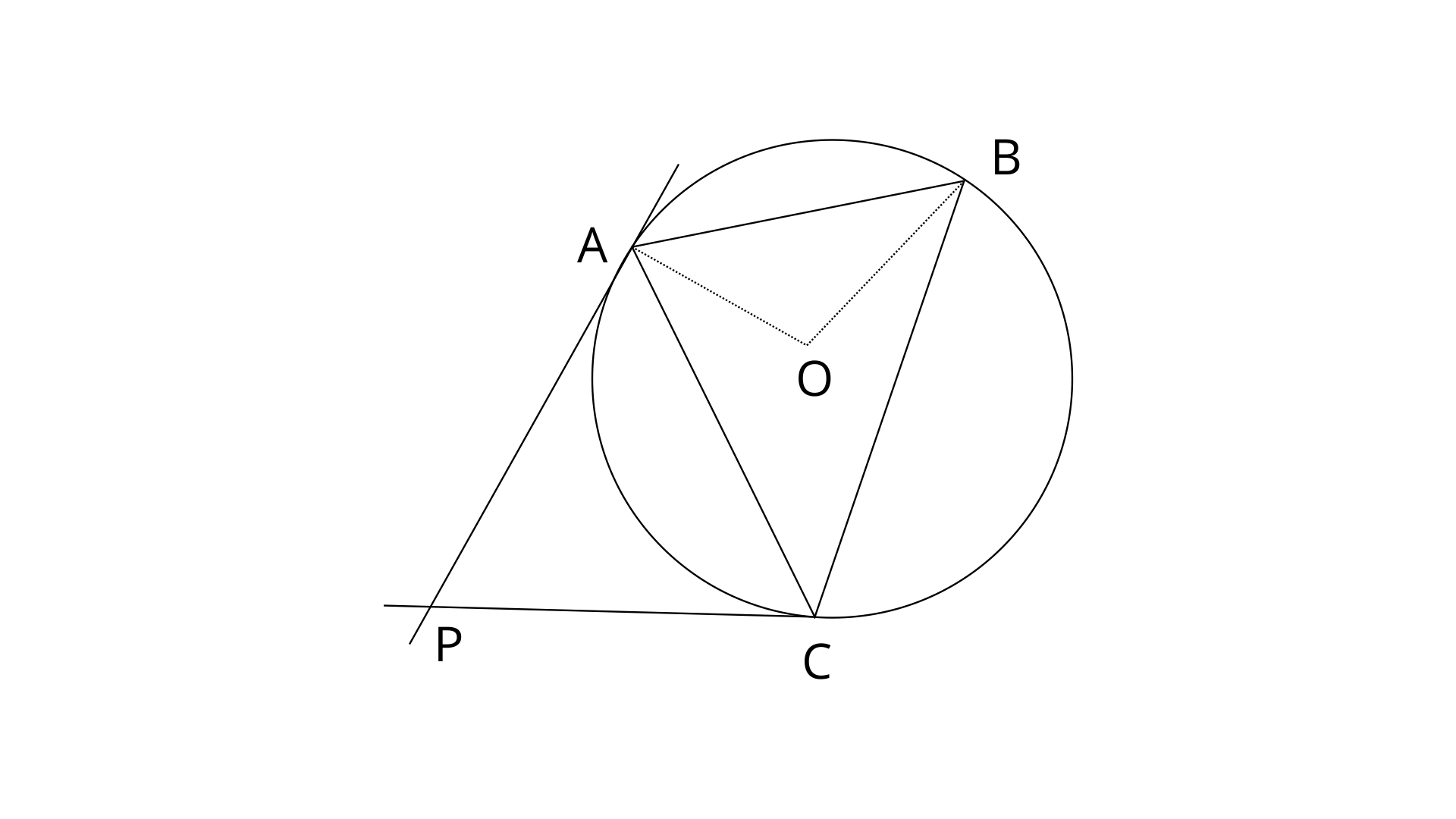
Ans: Join points OC.
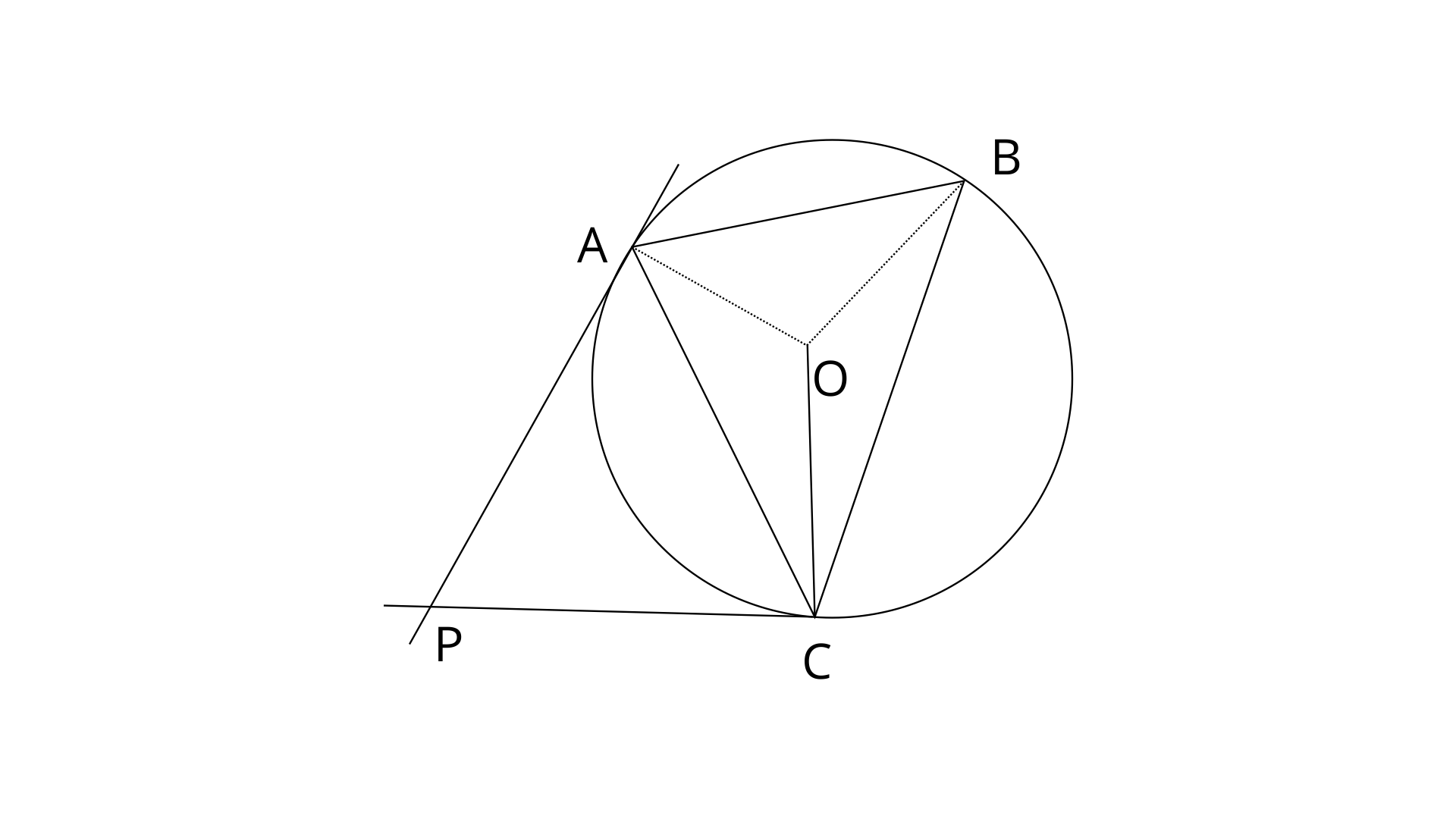
PA and PC are two tangents to the circle at points A and C.
In quadrilateral APCO,
Now,
Angle at the centre is doubled the angle at the circumcentre subtended by the same chord. Here
Therefore,
24. In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of
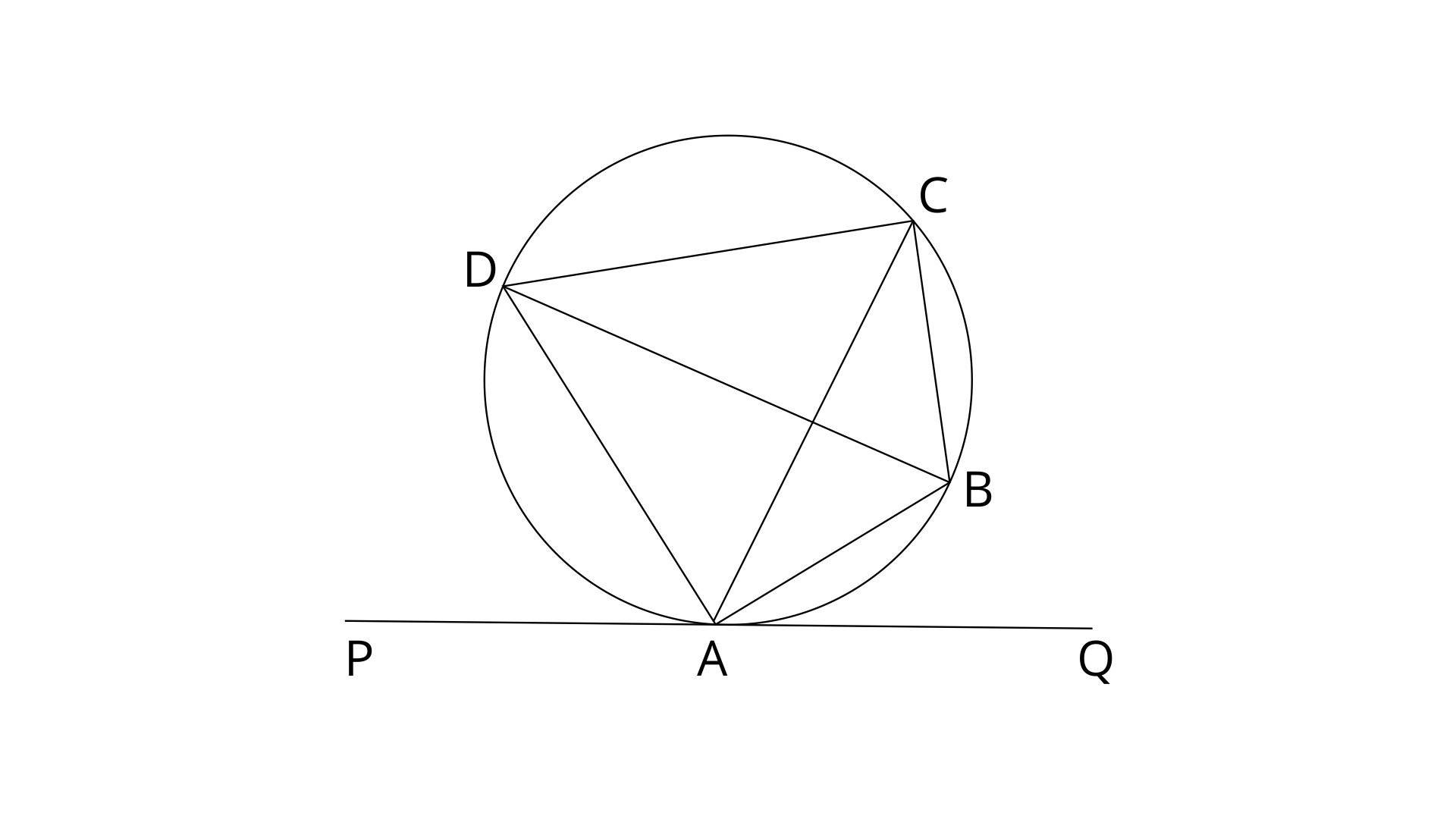
Ans: Since PQ is tangent to the circle at point A.
AB is bisector of
Therefore,
Since PQ is a straight line.
Hence,
AD is bisector of
Now,
Thus we can say
Therefore, BD is the diameter of the circle.
Exercise 18.2
1. (i) In the given figure,
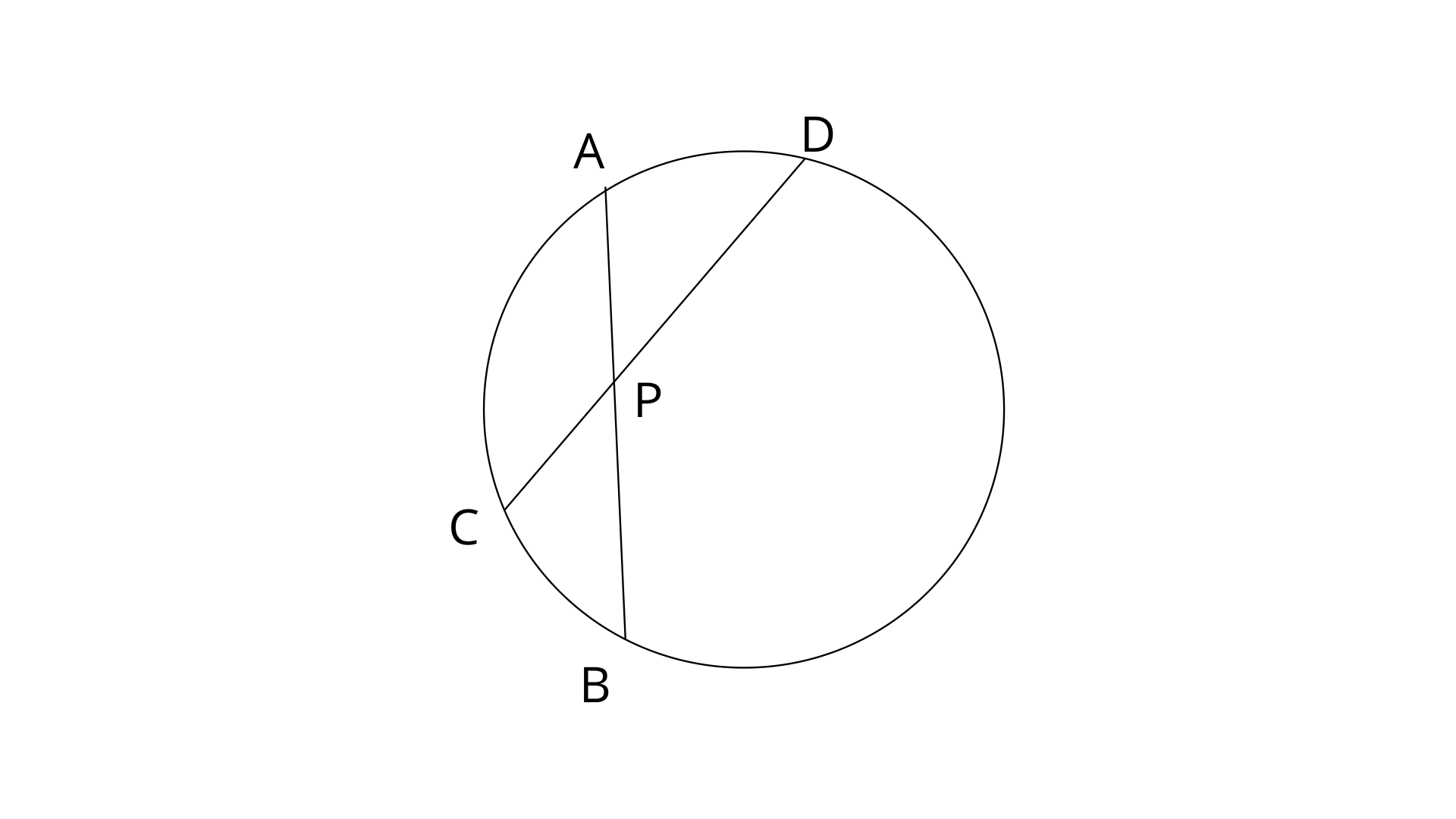
Ans:
Given that
Since two chords AB and CD intersect at point P.
Therefore,
Thus the value of PB is
(ii). In the given figure,
Ans: Given that
And,
Since two chords intersect each other at point P.
Therefore,
Now,
Thus the value of
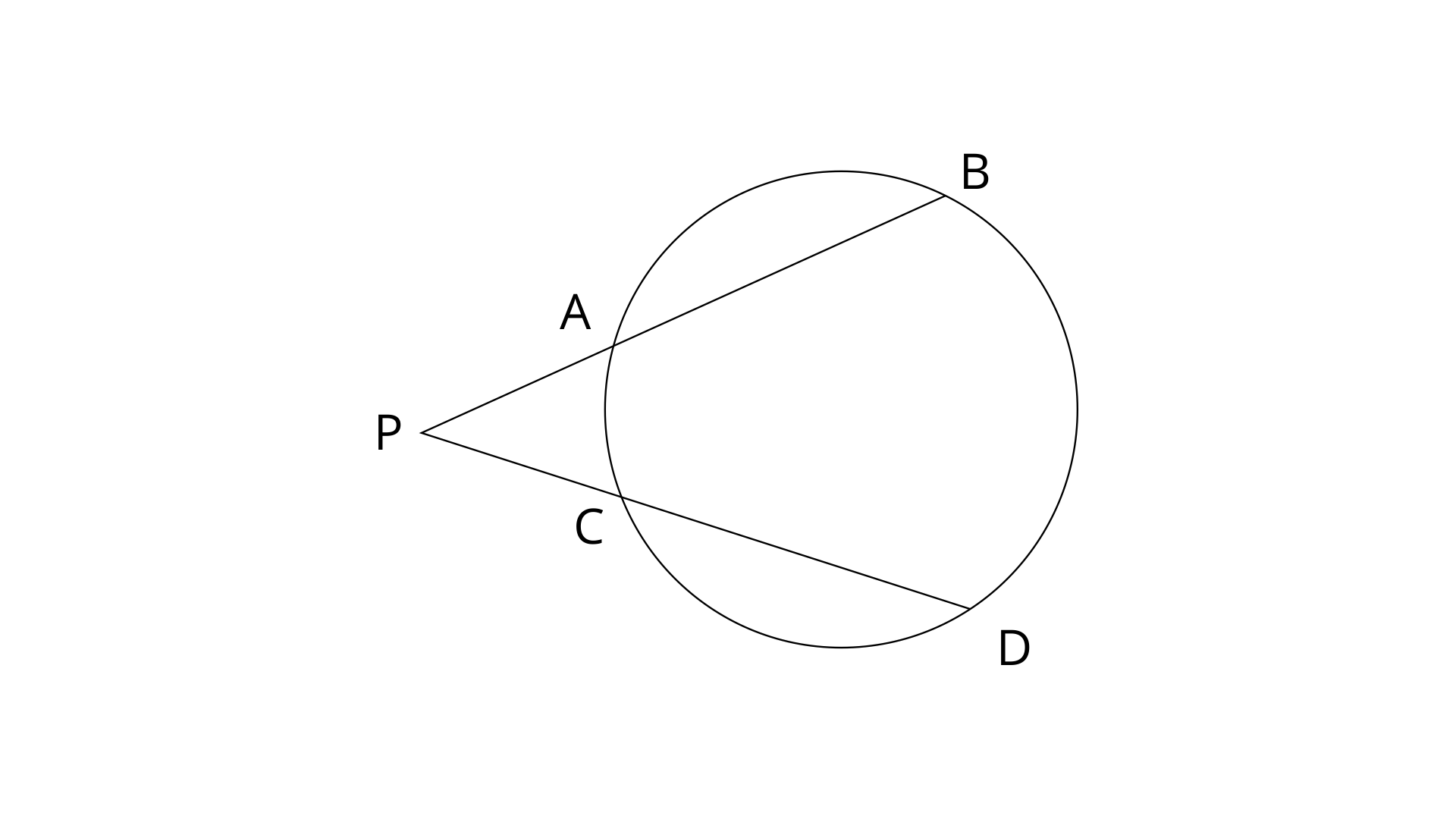
(iii). In the given figure, tangent
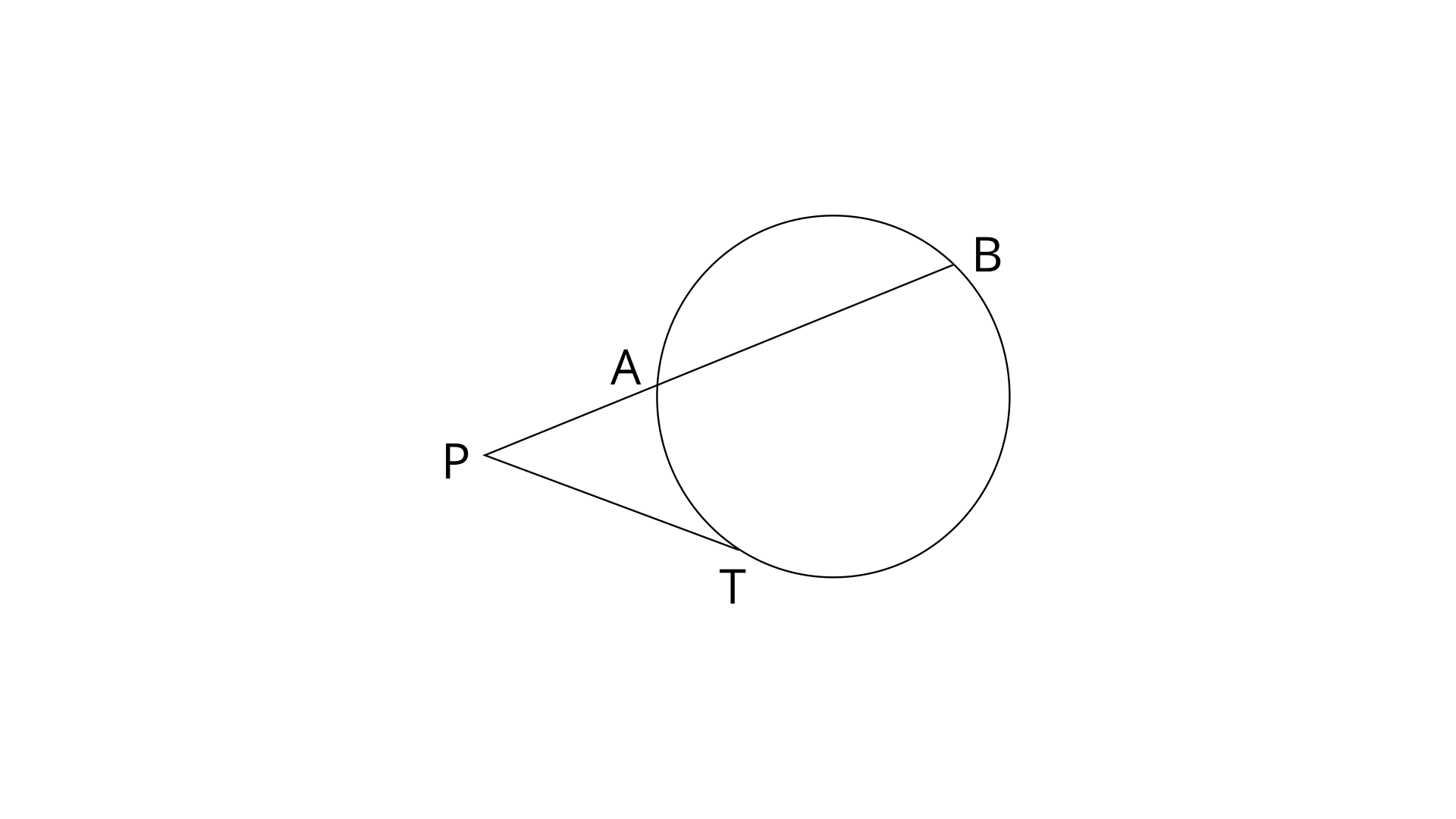
Ans: PAB is the secant and PT is the tangent, both intersect each other externally at point P.
Now,
2. In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD=7.8cm, PD=5cm, PB=4cm. Find :
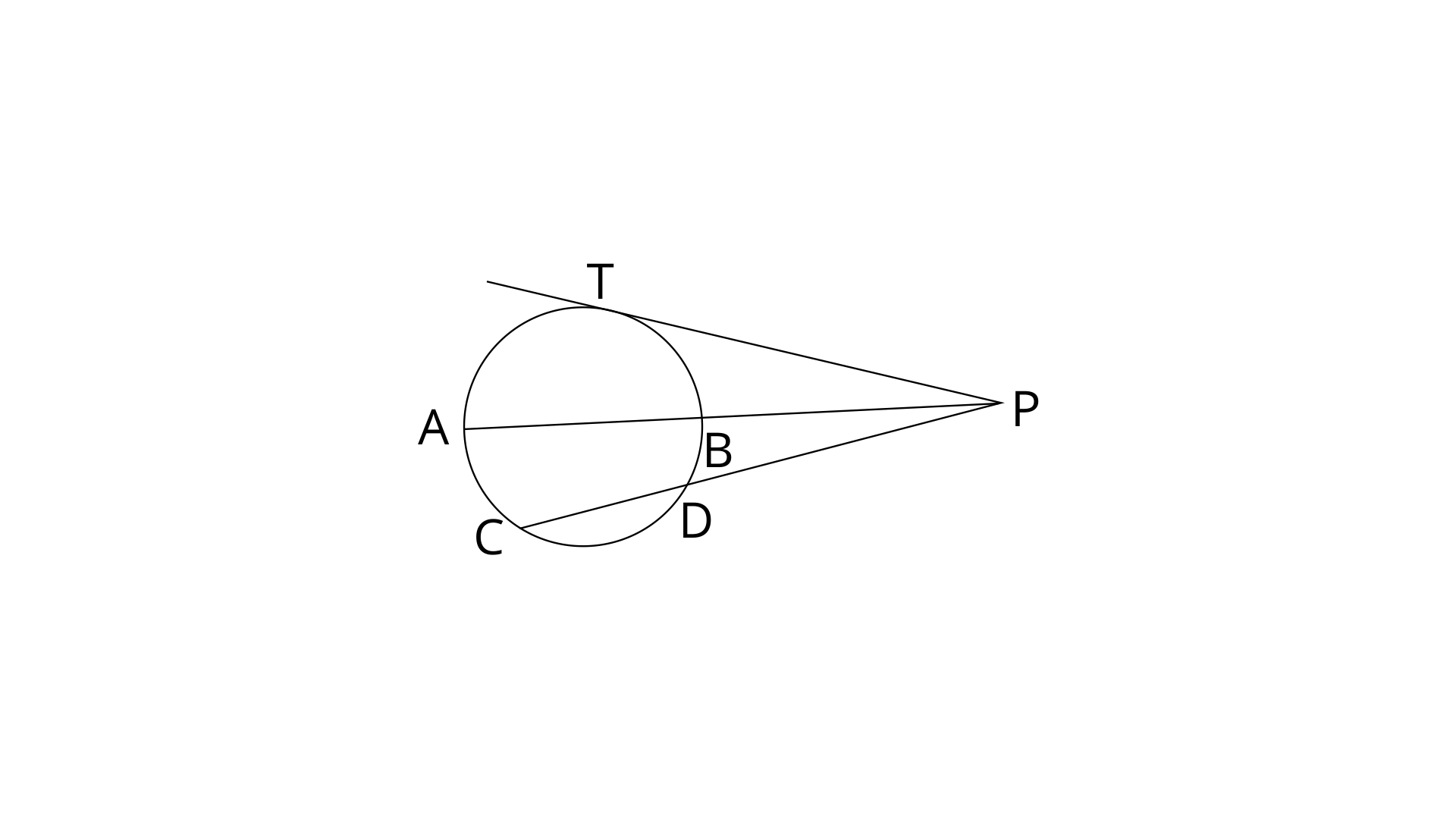
(i). AB
Ans: Chords AB and CD intersect externally at point P.
Therefore,
Now substituting these values in eq. (1)
Thus the value of AB is 12cm.
(ii). The length of the tangent
Ans: Tangent PT and chord CD intersect each other externally at point P.
Therefore,
Thus the length of the tangent is 8cm.
3. In the following figure, PQ is tangent to the circle at A, DB is the diameter and O is the centre of the circle. If
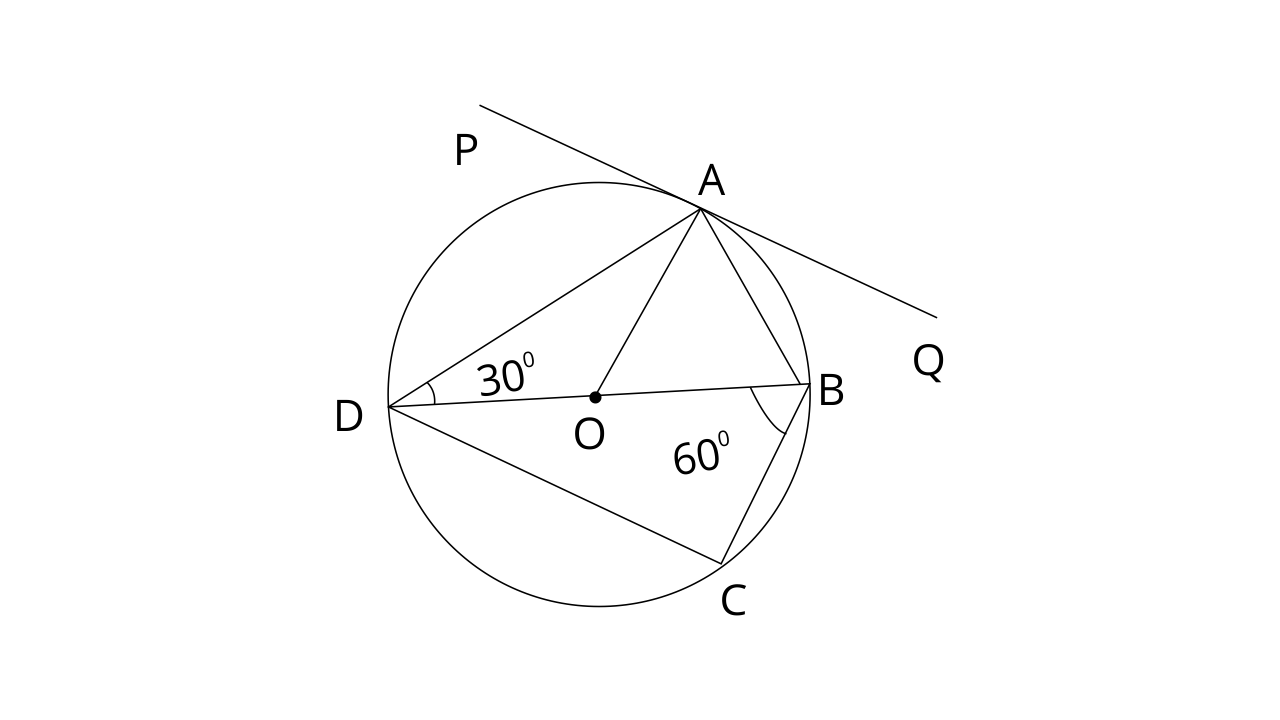
(i).
Ans: In a circle, Angle subtended by the diameter at the circumference is the right angle. Therefore,
In
OA=OB (Radii of same circle)
Now, in
Thus the value of
(ii).
Ans: Since, OD=OA(Radii of same circle)
OA is radius and PQ is tangent. Radius is perpendicular to the tangent.
Therefore,
Thus the value of
(iii).
Ans: BD is diameter of the circle and
Now by using angle sum property in
Thus the value of
4. If PQ is a tangent to the circle at R; calculate :
(i).
(ii).
Given O is the centre of the circle and angle
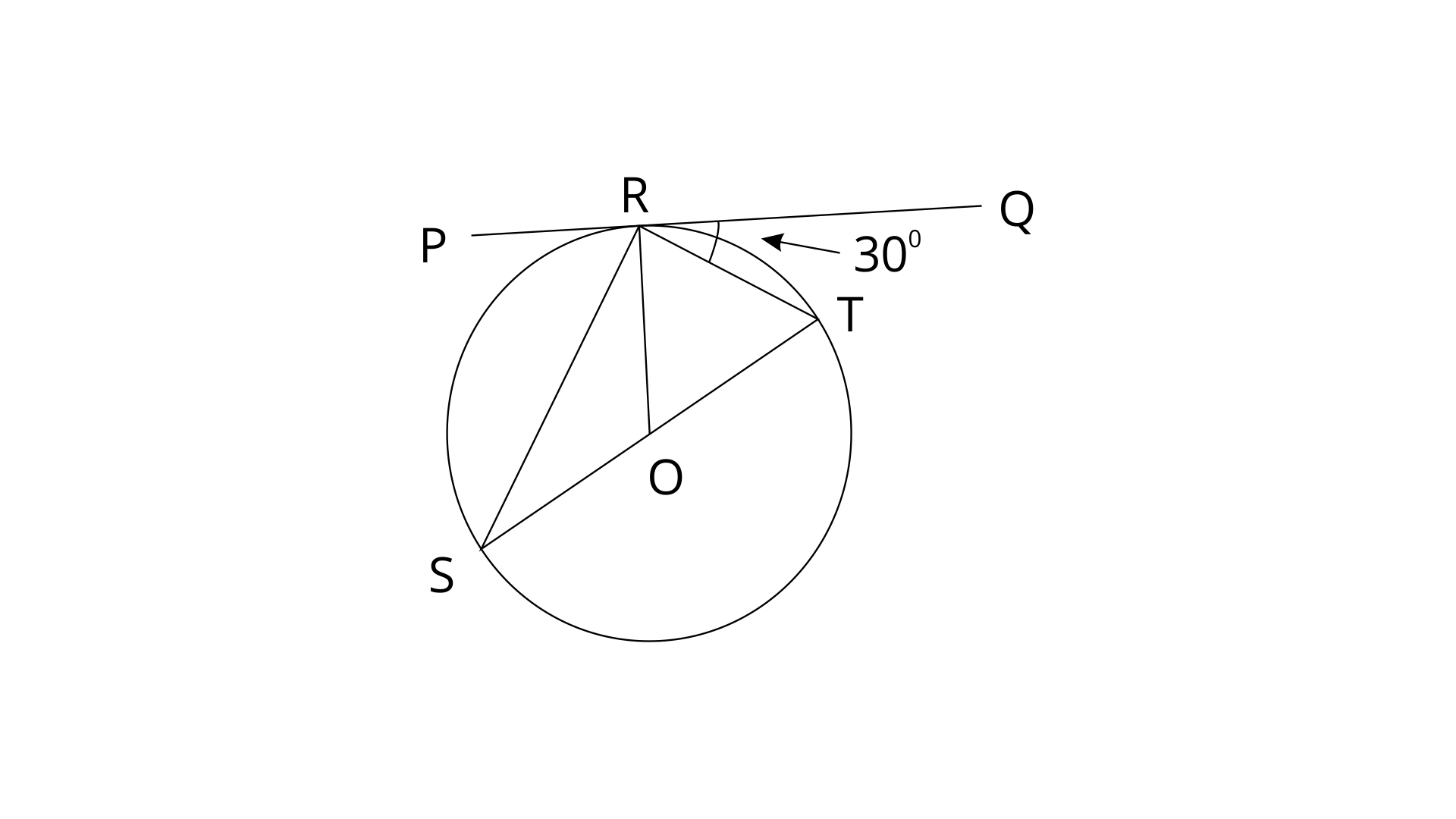
(i).
Ans: In a circle, Angle at the circumference subtended by the diameter is the right angle. Therefore,
PQ is a straight line.
Thus the value of
(ii).
Ans: PQ is tangent and OR is radius. Radius is perpendicular to the tangent.
Therefore,
OR=OT(Radii of same circle)
Now, By using angle sum property in
Thus the value of
5. AB is the diameter and AC is a chord of a circle with centre O such that angle
Ans:
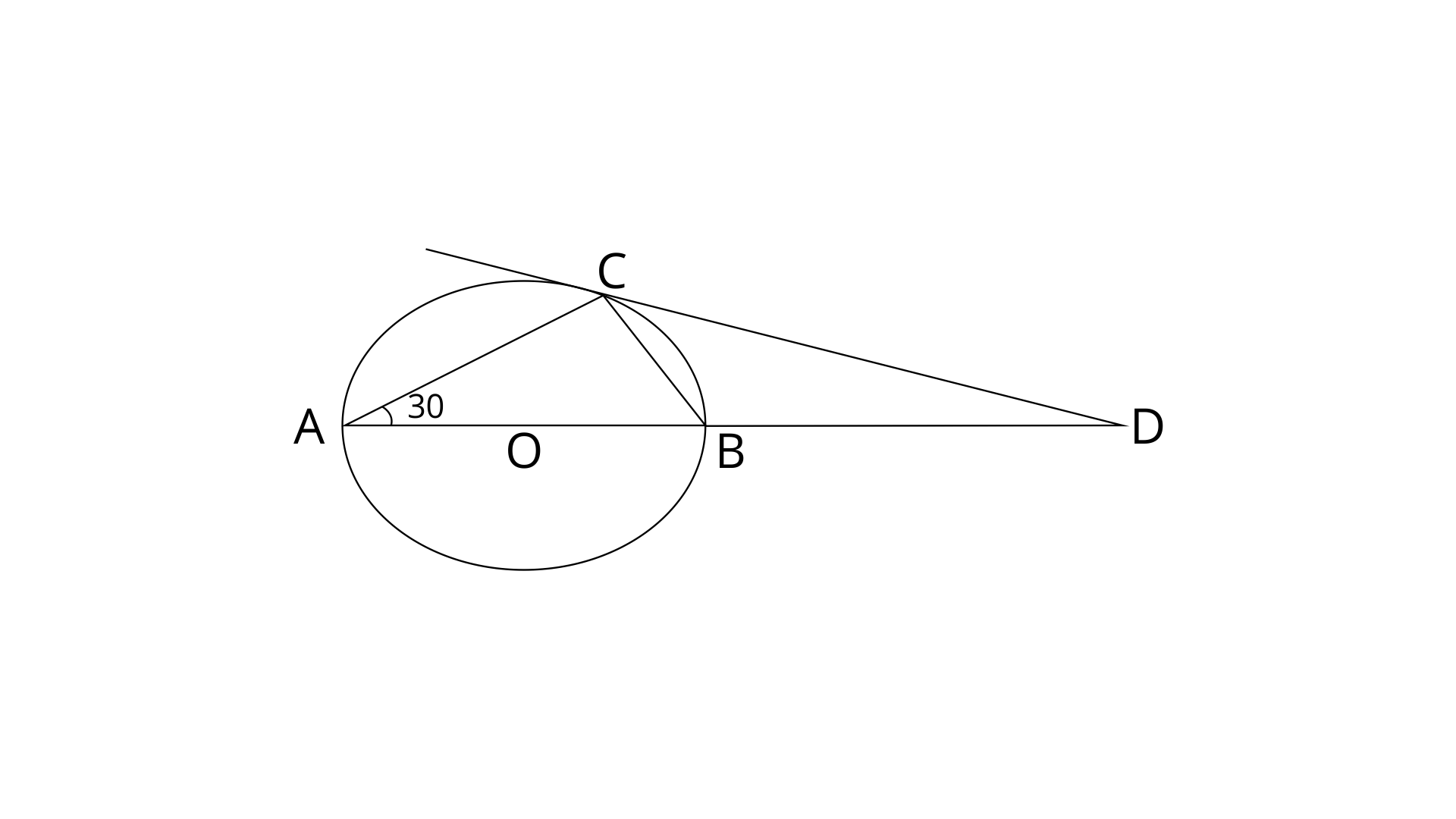
OA=OC (Radii of same circle)
In
AB is diameter and a straight line.
In a circle, Angle at the circumference subtended by the diameter is the right angle.
Therefore,
By using angle sum property in
From eq. (1) and (2)
Hence proved.
6. Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR show that
Ans:
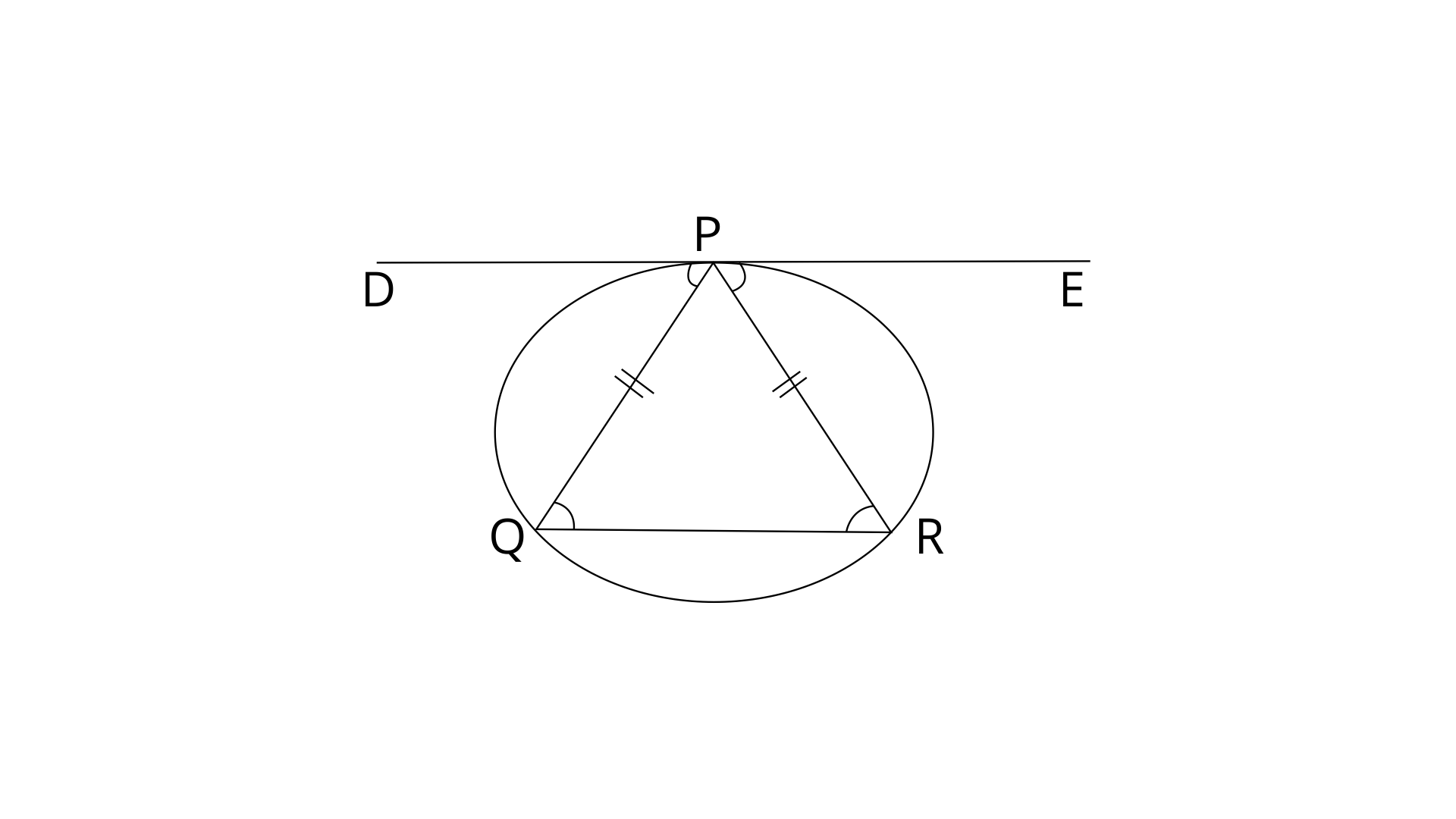
DE is tangent to the circle at point P.
DE||QR
Therefore,
Since DP is a tangent and PQ is chord such as PQ=PR
Therefore,
From eq.(1),(2) and (3)
PQ=PR (opposite sides of equal angles)
Therefore
7. Two circles with centres O and O’ are drawn to intersect each other at points A and B. centres O of the circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O’ at A. Prove that OA bisects angle BAC.
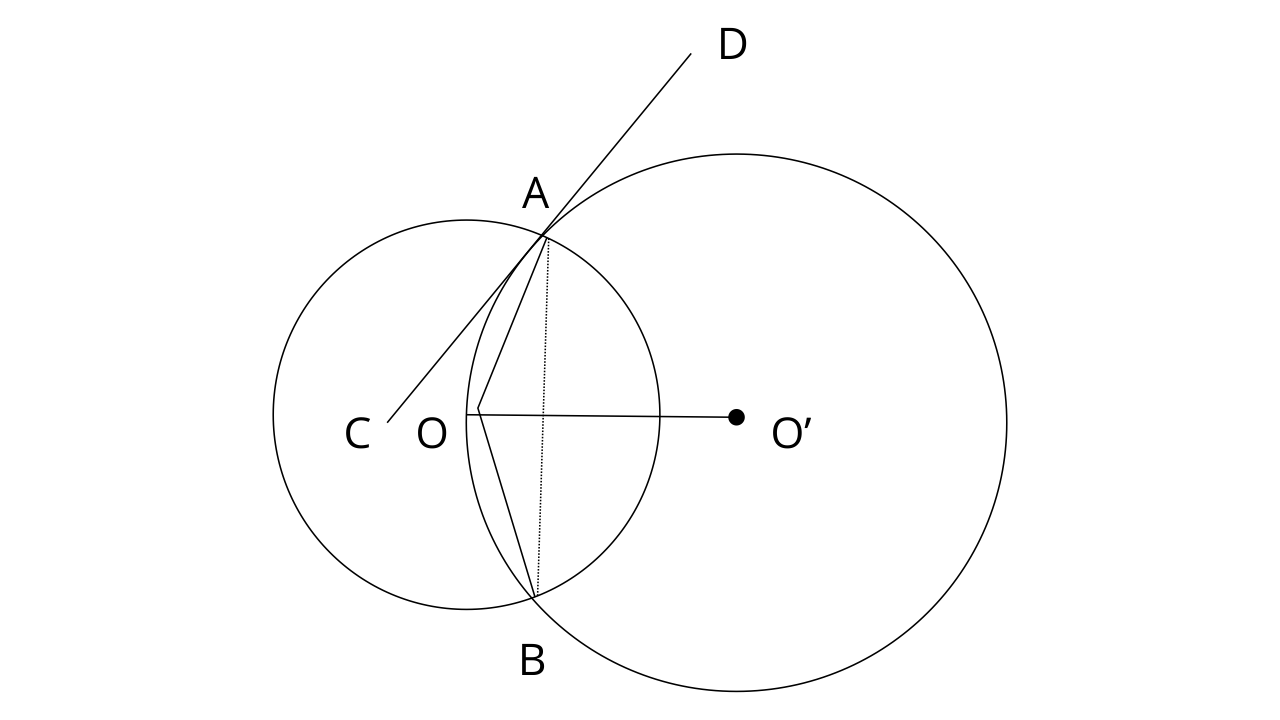
Ans: CD is a tangent to the circle and AO is chord.
Therefore,
Since, OA=OB (Radii of same circle)
Therefore,
From eq. (1) and (2)
Therefore OA is angle bisector of
8. Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that :
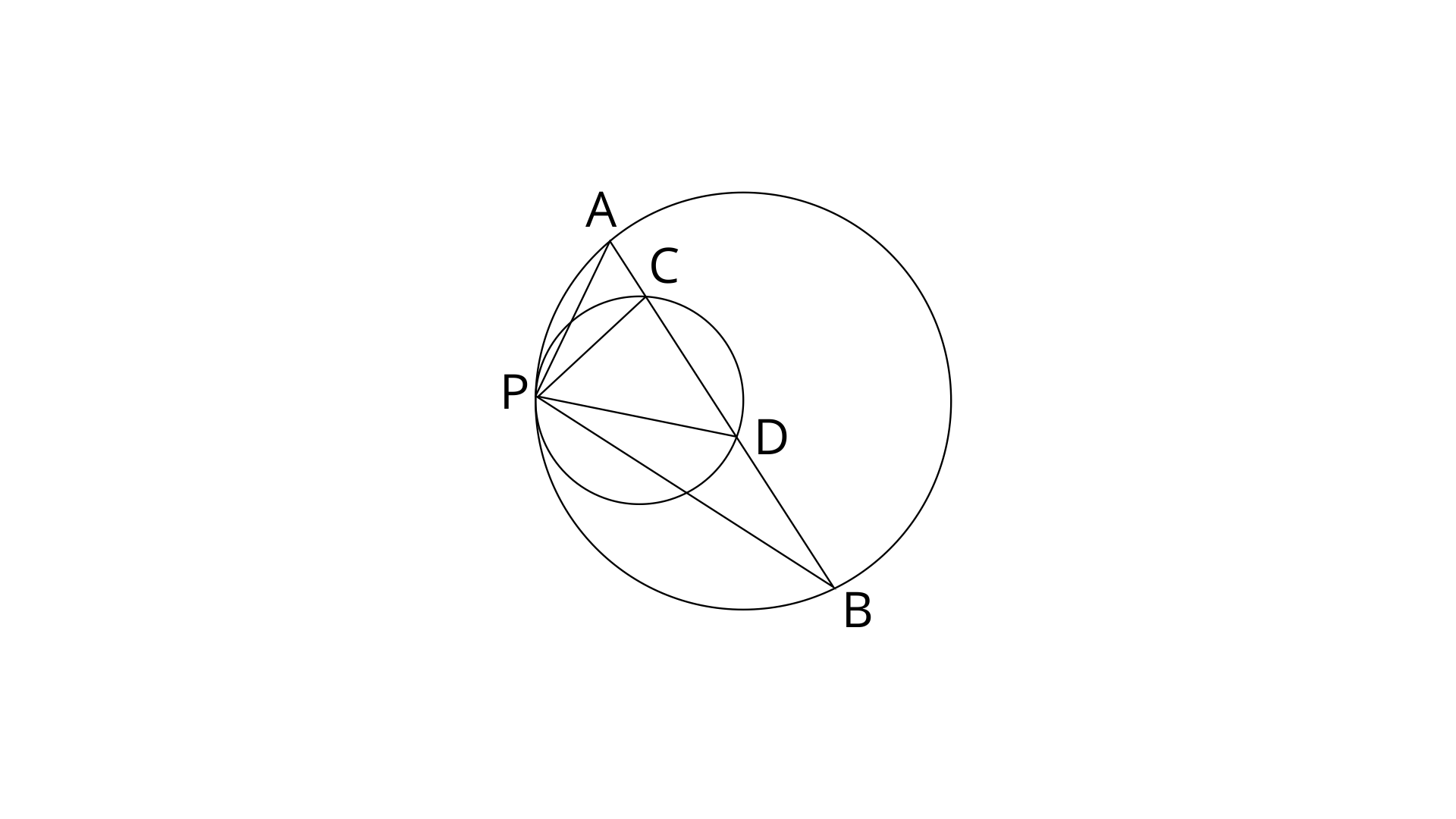
Draw tangent at point P.
Ans: We draw a tangent TS at P.
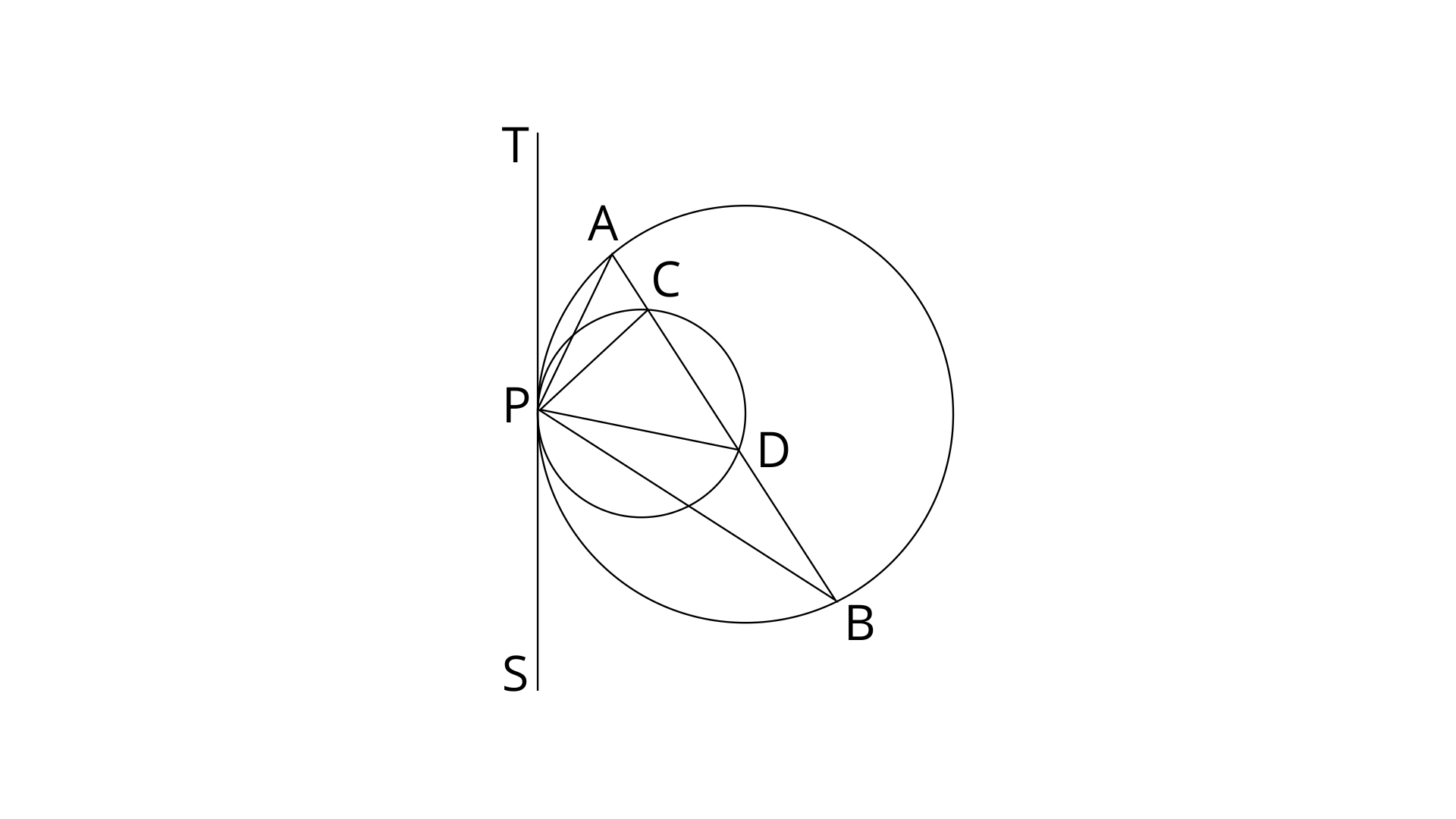
TPS is a tangent and PB is a chord.
Similarly,
Subtract eq. (1) from eq. (2)
By using exterior angle property in
Now on substituting the value from eq.(4) in eq.(3)
(Hence proved)
9. In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Ans:
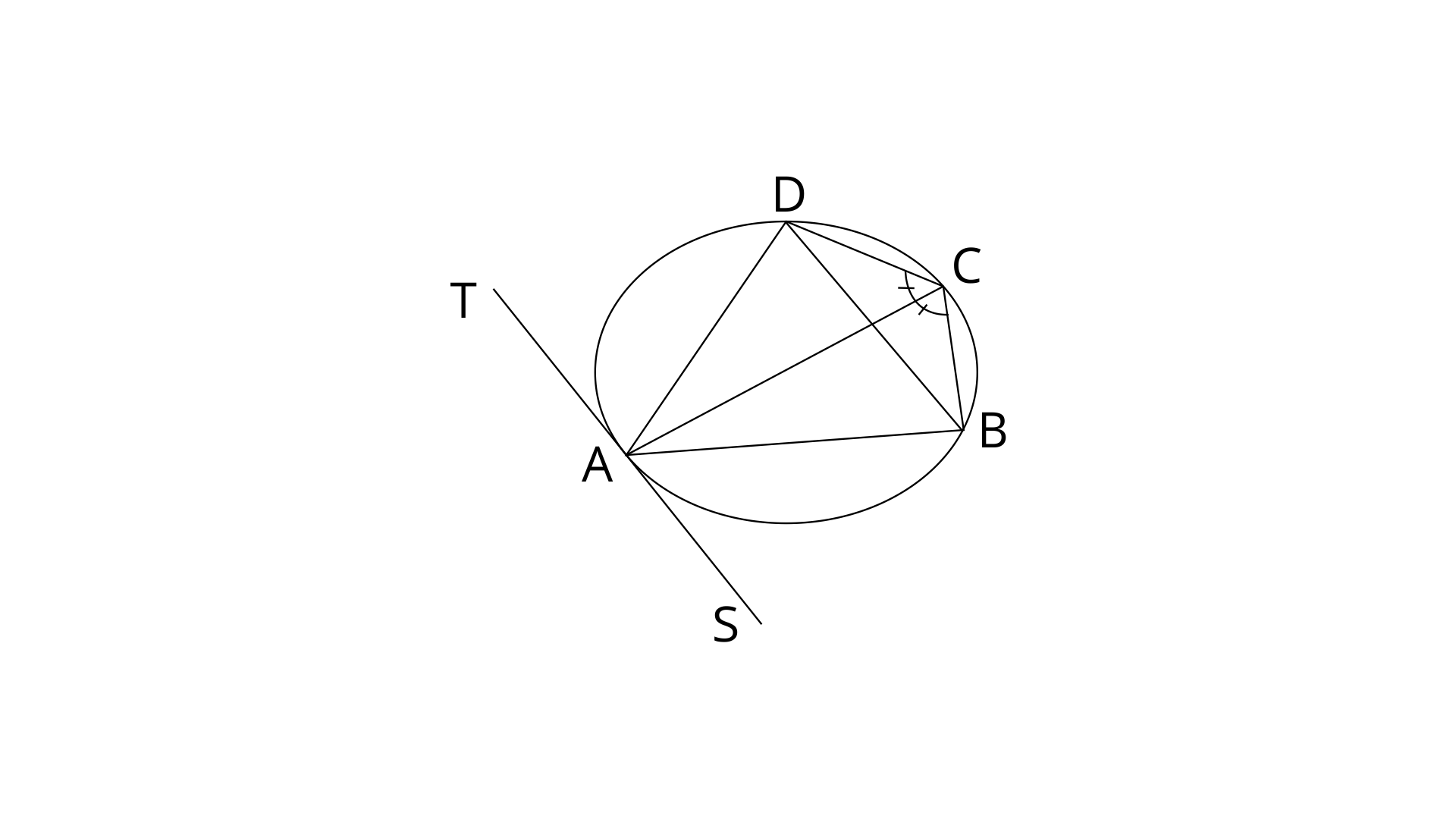
In a circle, Angles at the circumference subtended by the same chord are equal.
Similarly,
AC is angle bisector of
From eq. (1), (2) and (3)
TAS is a tangent and AB is a chord.
Therefore,
Since,
Therefore,
If two alternate angles are equal then the sides are equal.
Therefore TAS is parallel to BD.
10. In the figure, ABCD is a cyclic quadrilateral with BC=CD. TC is tangent to the circle at point C and DC is produced to point G. If
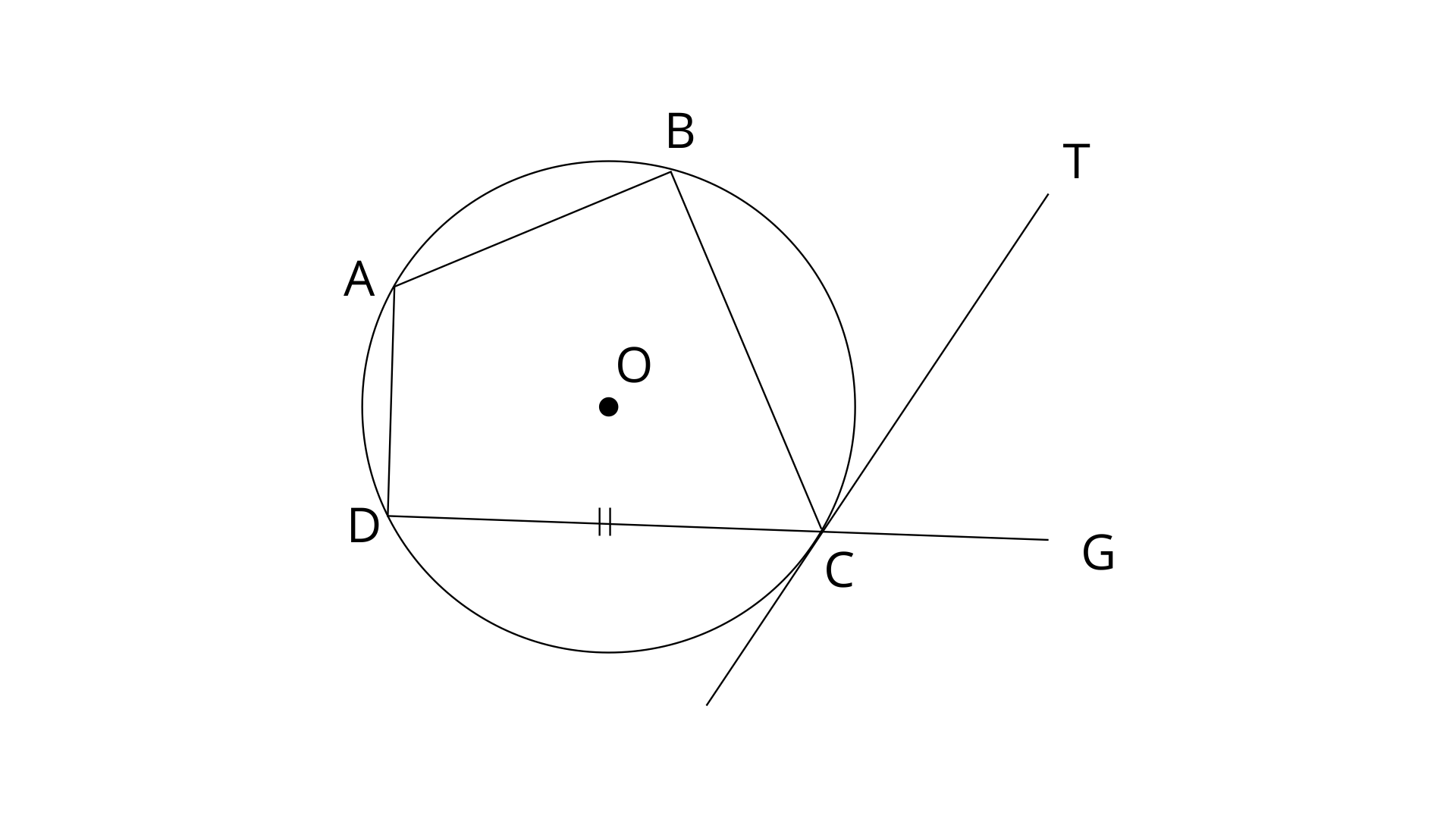
(i). Angle BCT
(ii). Angle DOC
Ans: Join AC and OD.
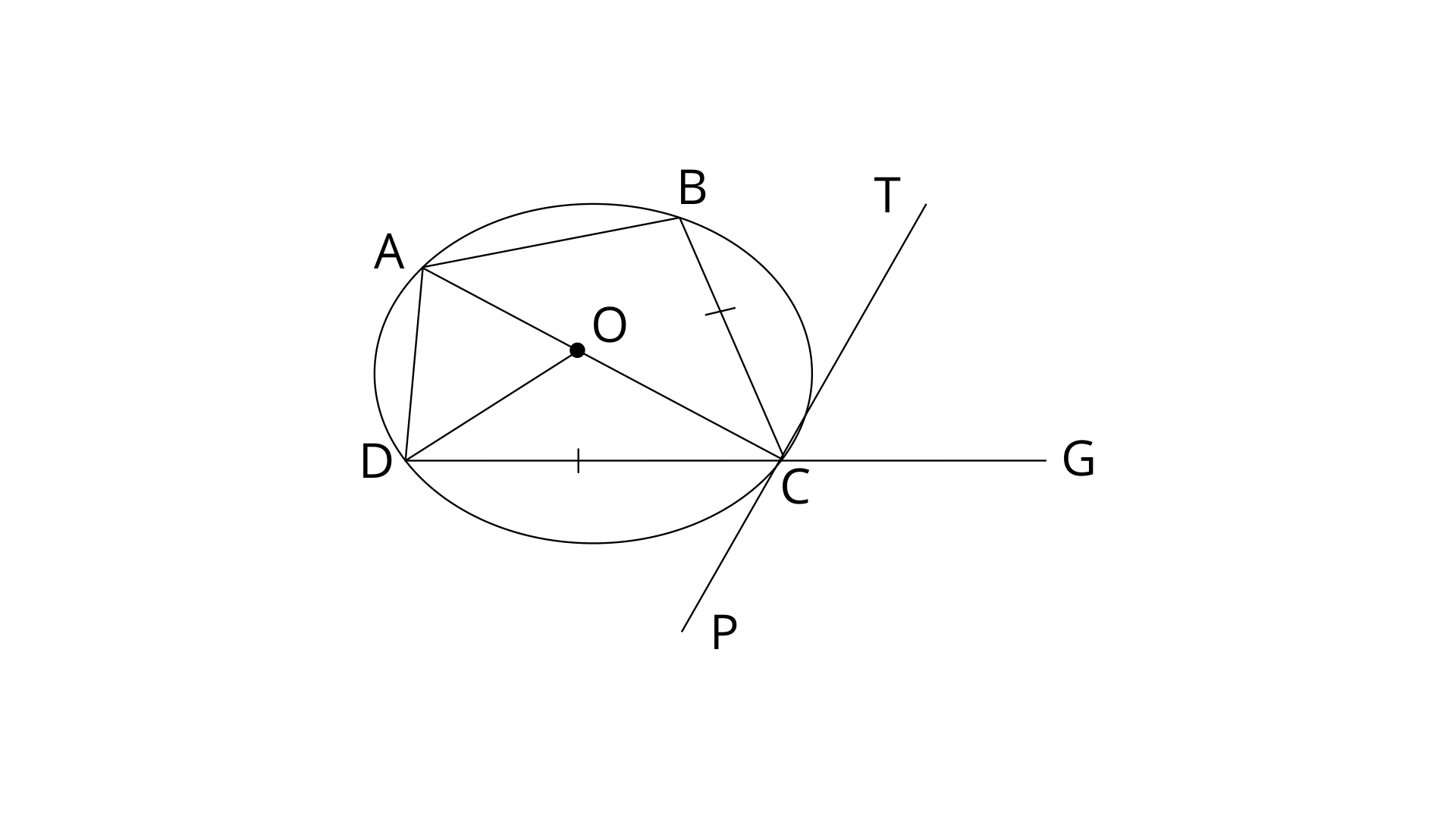
DCG is a straight line.
Here BC=CD
Angles opposite to equal sides are equal.
PCT is a straight line.
Thus the value of
(ii). Angle DOC
Ans: Since
PT is tangent and DC is chord.
In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord. Here
Thus the value of
11. Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concyclic.
Ans: Join AB, PB and BQ.
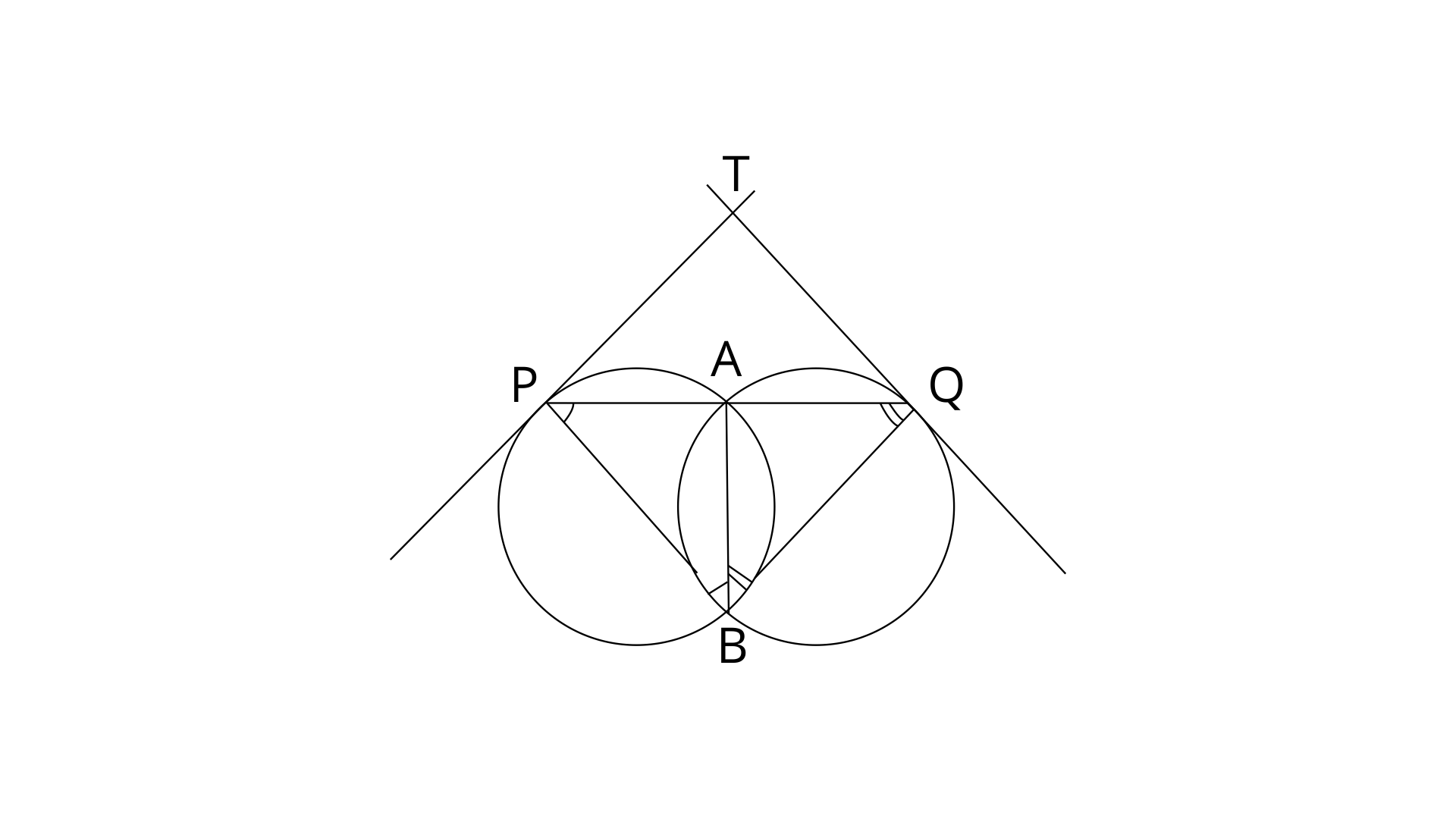
TP is the tangent and AB is a chord.
Similarly,
On adding equations (1) and (2)
By using angle sum property in
From eq.(1) and (2) by putting
Since
12. In the figure; PA is tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that :
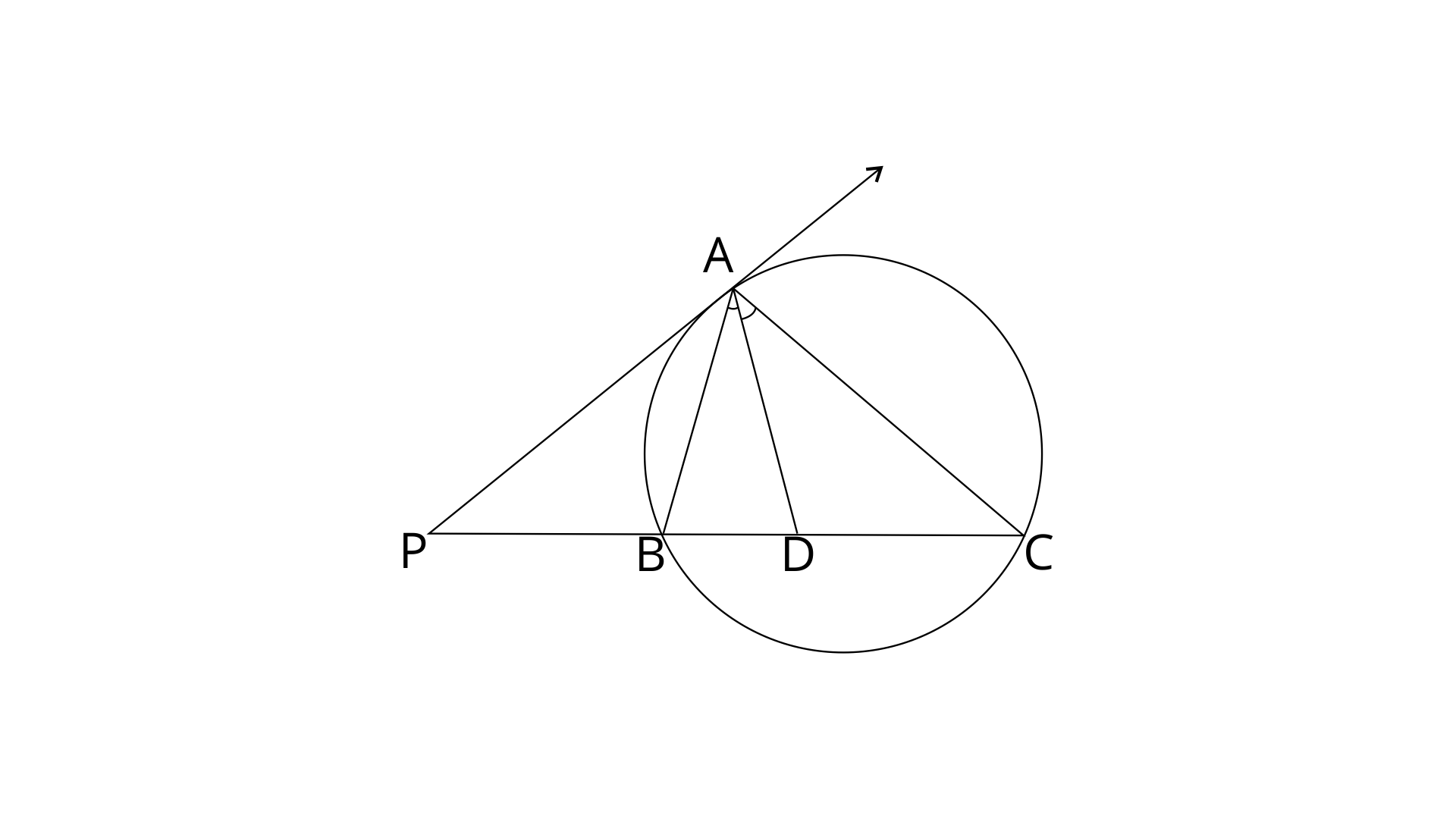
Ans:
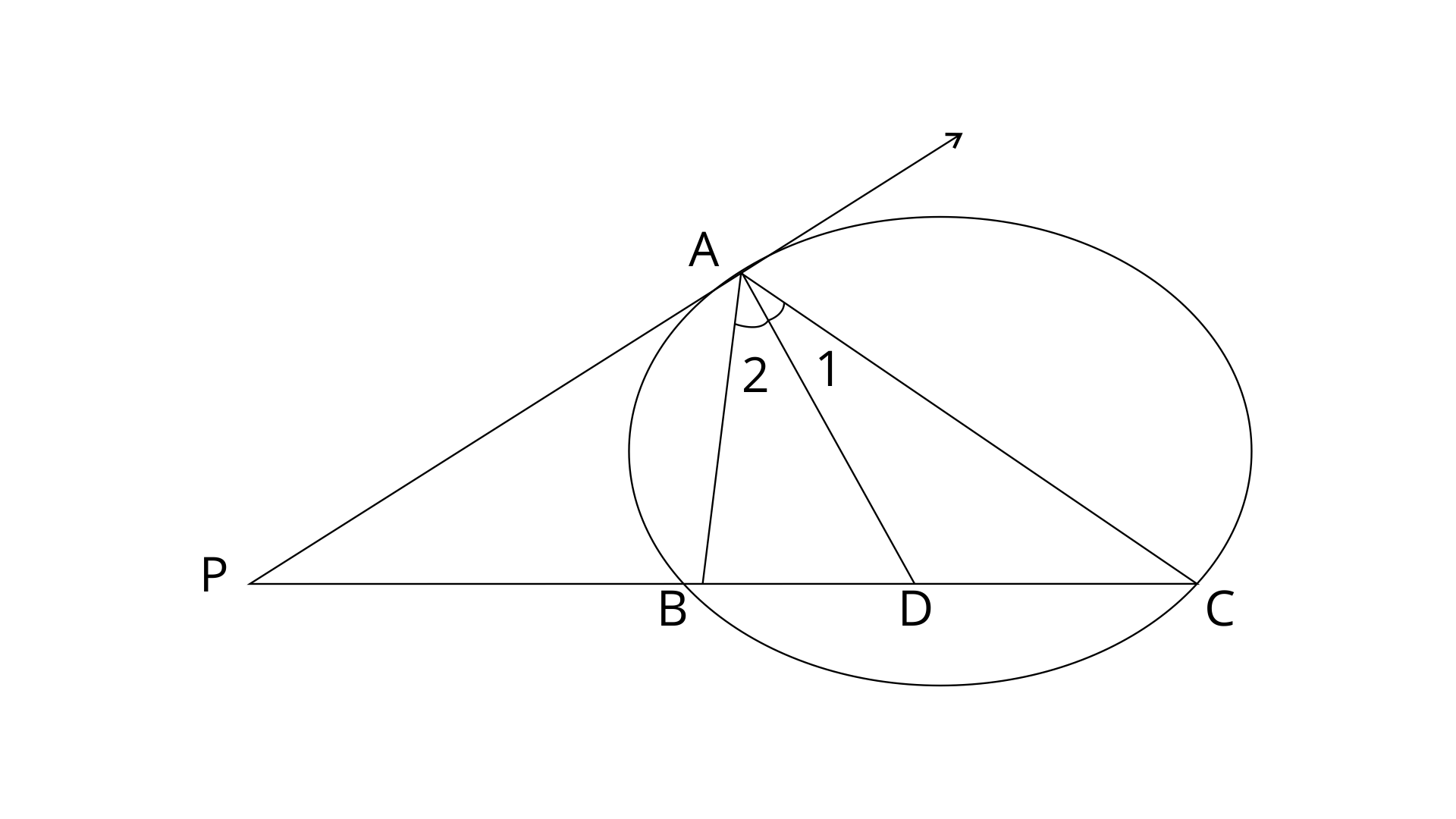
PA is tangent to the circle and AB is chord.
AD is bisector of angle BAC.
Therefore,
In
In
13. Two circles intersect each other at points A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
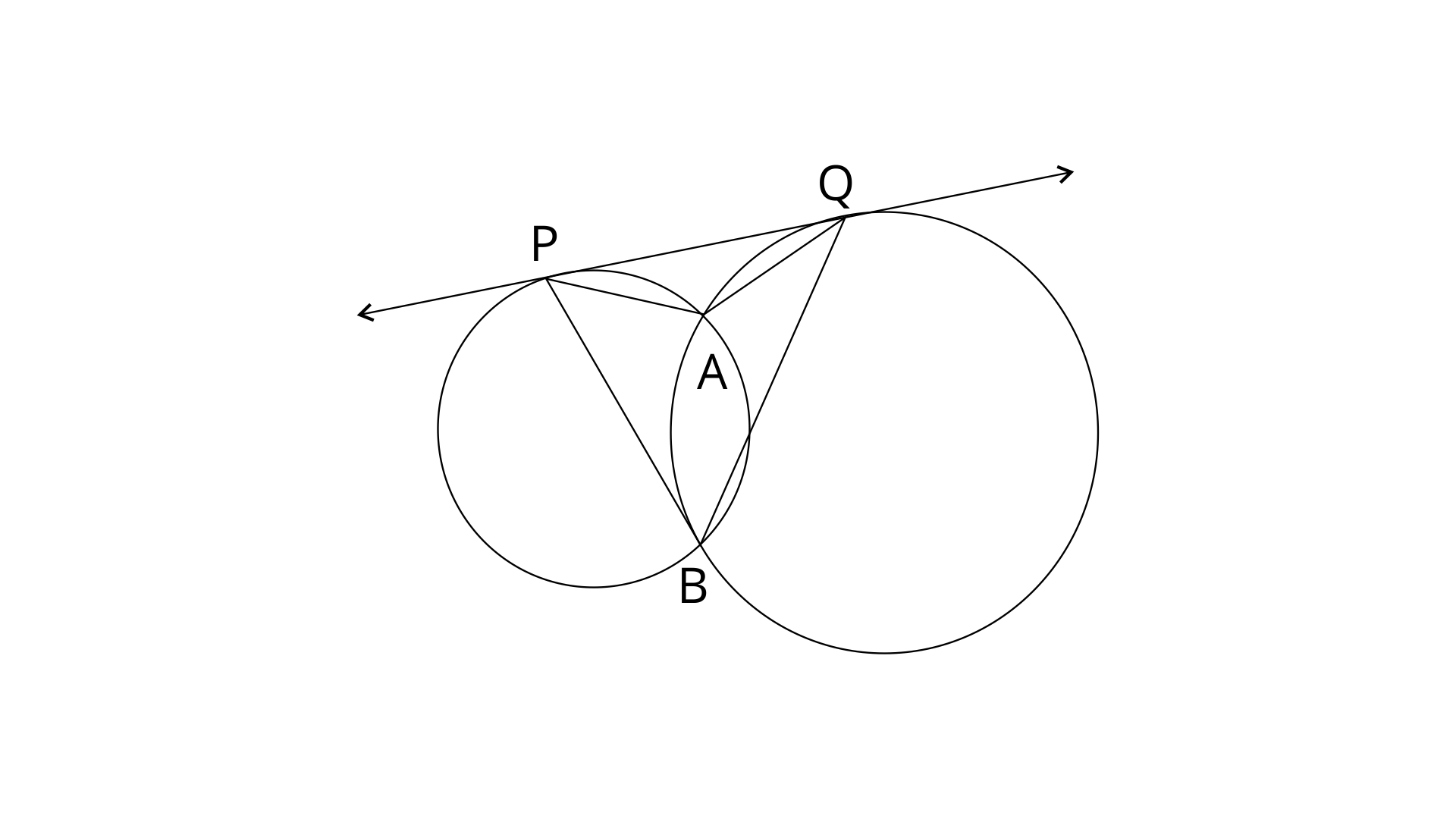
Ans: Join AB.

PQ is a tangent and AB is a chord.
On adding eq.(1) and (2)
In
PQA=\angle QBA$]-----(4)
From eq. (3) and (4)
Therefore,
14. In the figure, chords AE and BC intersect at each other at point D.
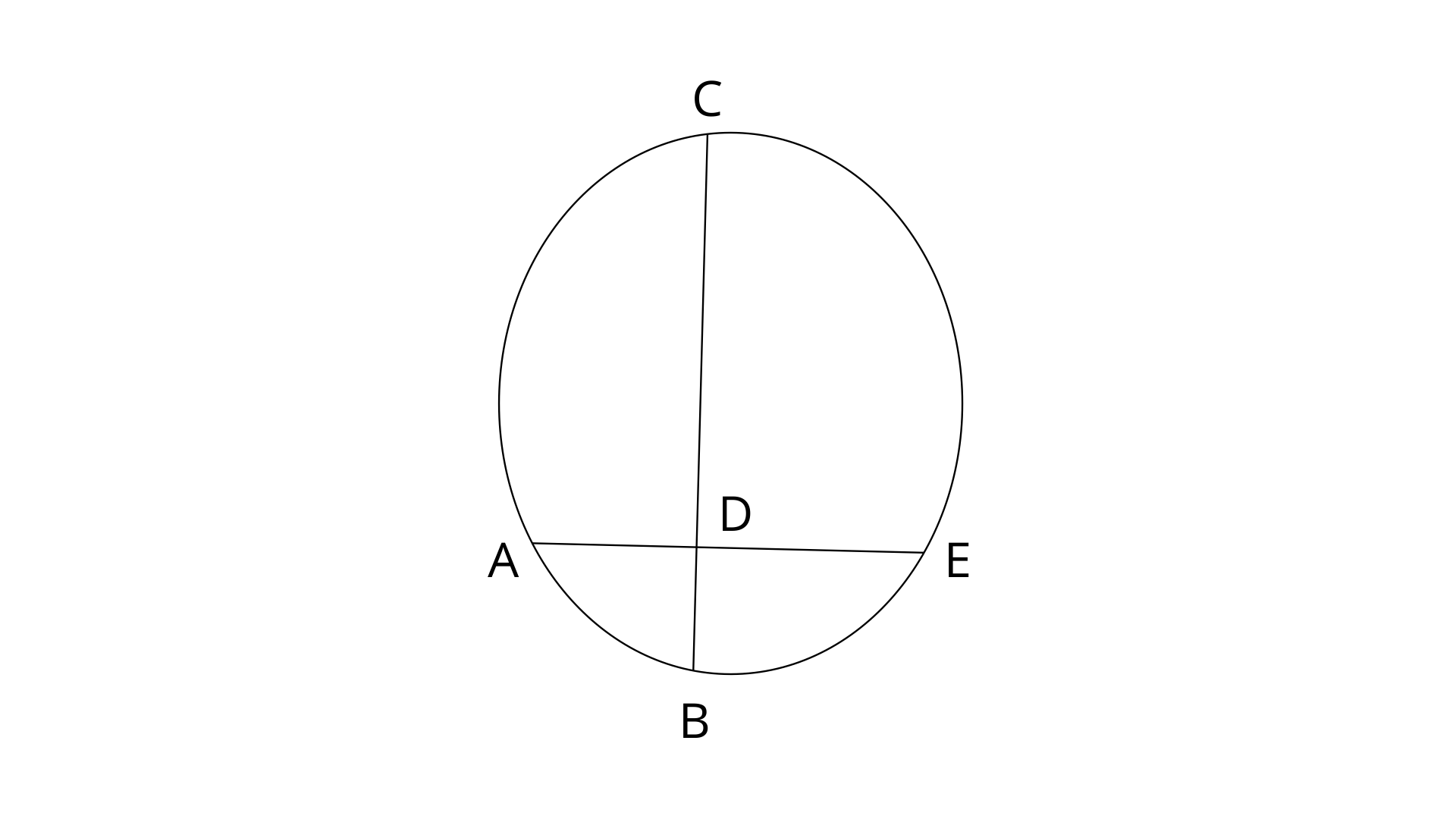
(i). If
(ii). If AD=BD, show that : AE=BC.
Ans:
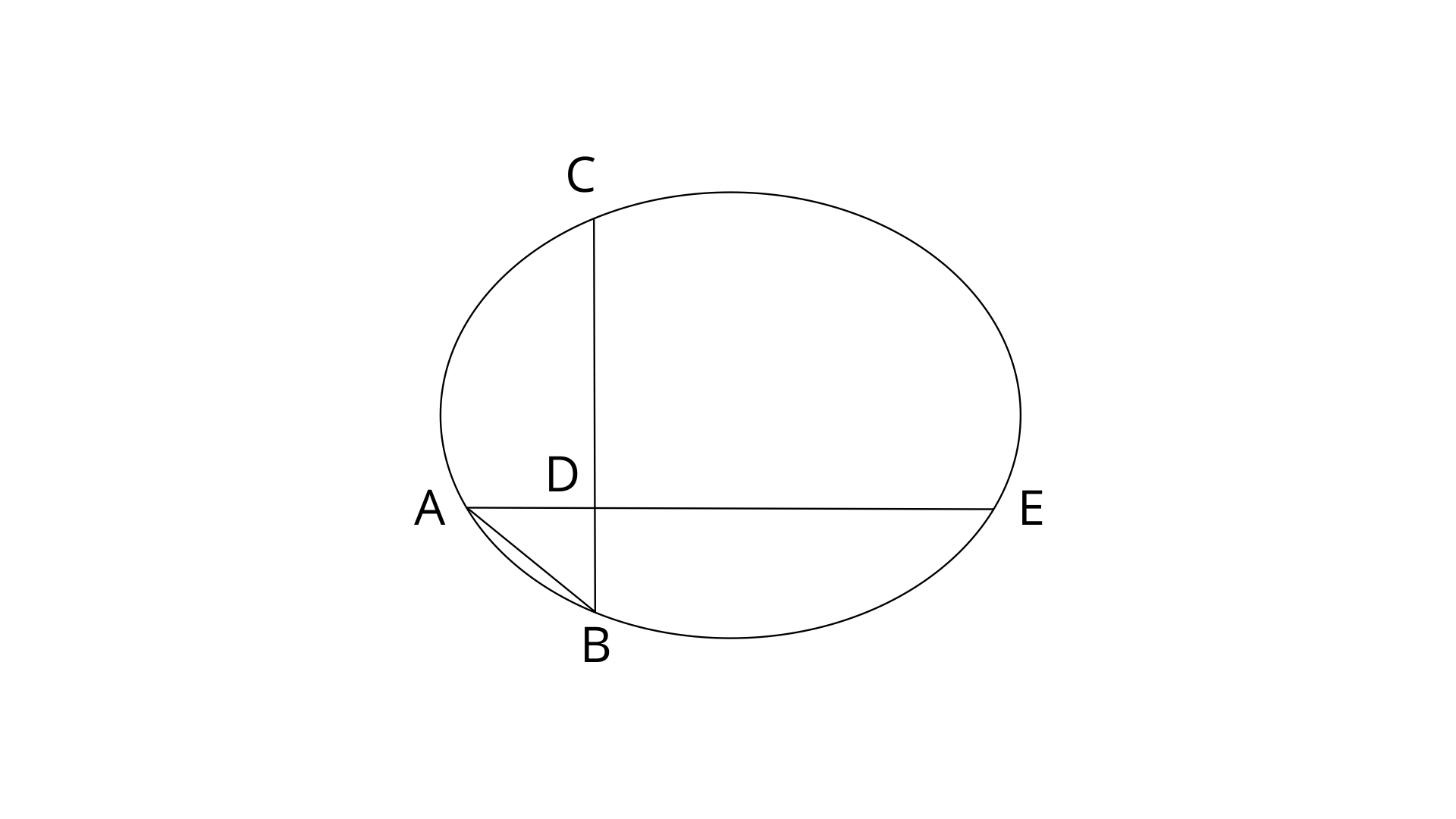
Join points AB.
(i). If
Ans: Since,
Chords AE and BC intersect each other at point D.
Thus the value of DE is 12cm.
(ii). If AD=BD, show that : AE=BC.
Ans: Since, AD=BD-------(1)
On adding eq.(1) and (2)
AD+DE=BD+CD
15. Circles with centres P and Q intersect at points A and B are shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent; show that : CE=BD.
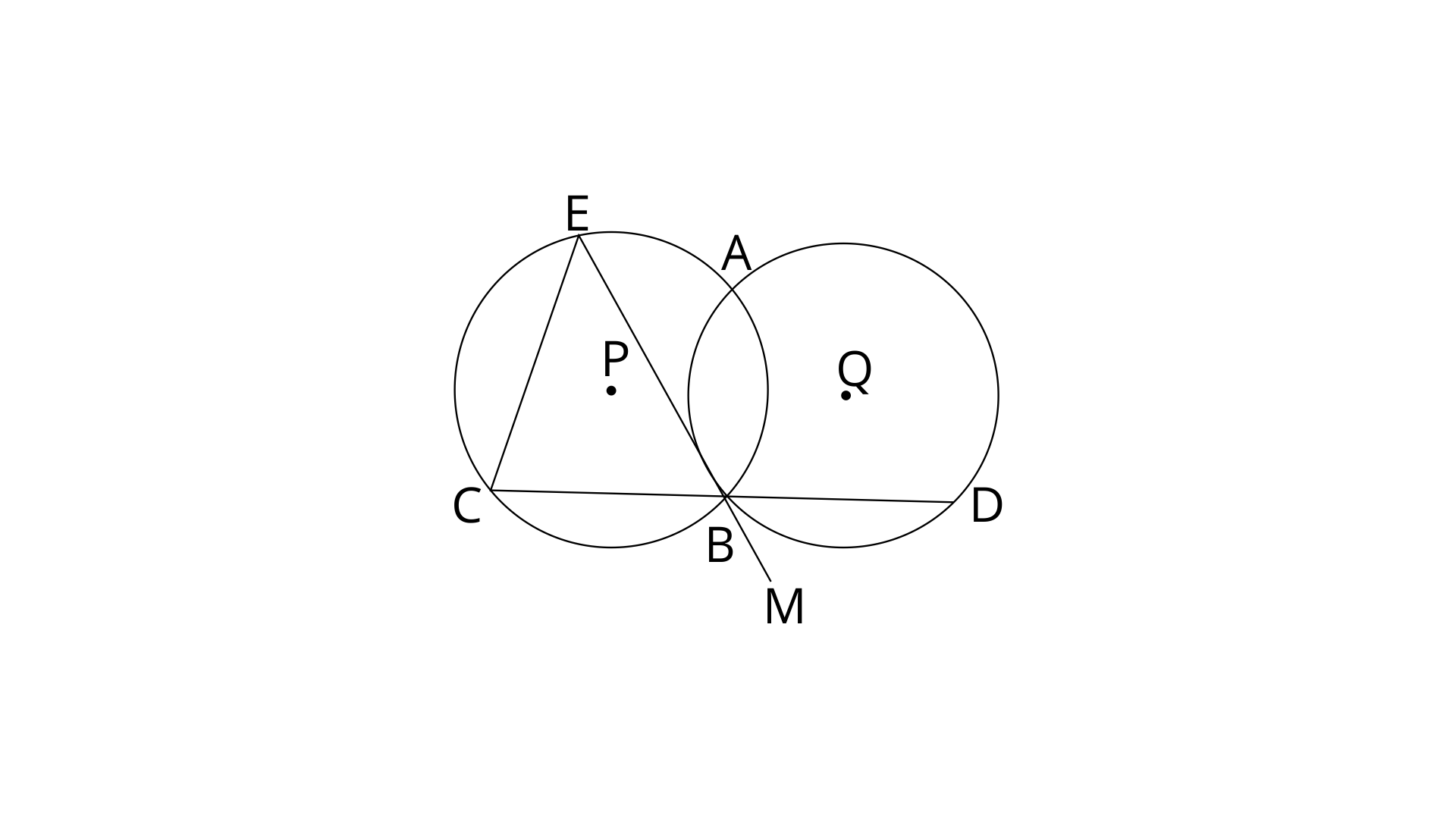
Ans: Join AB and AD.
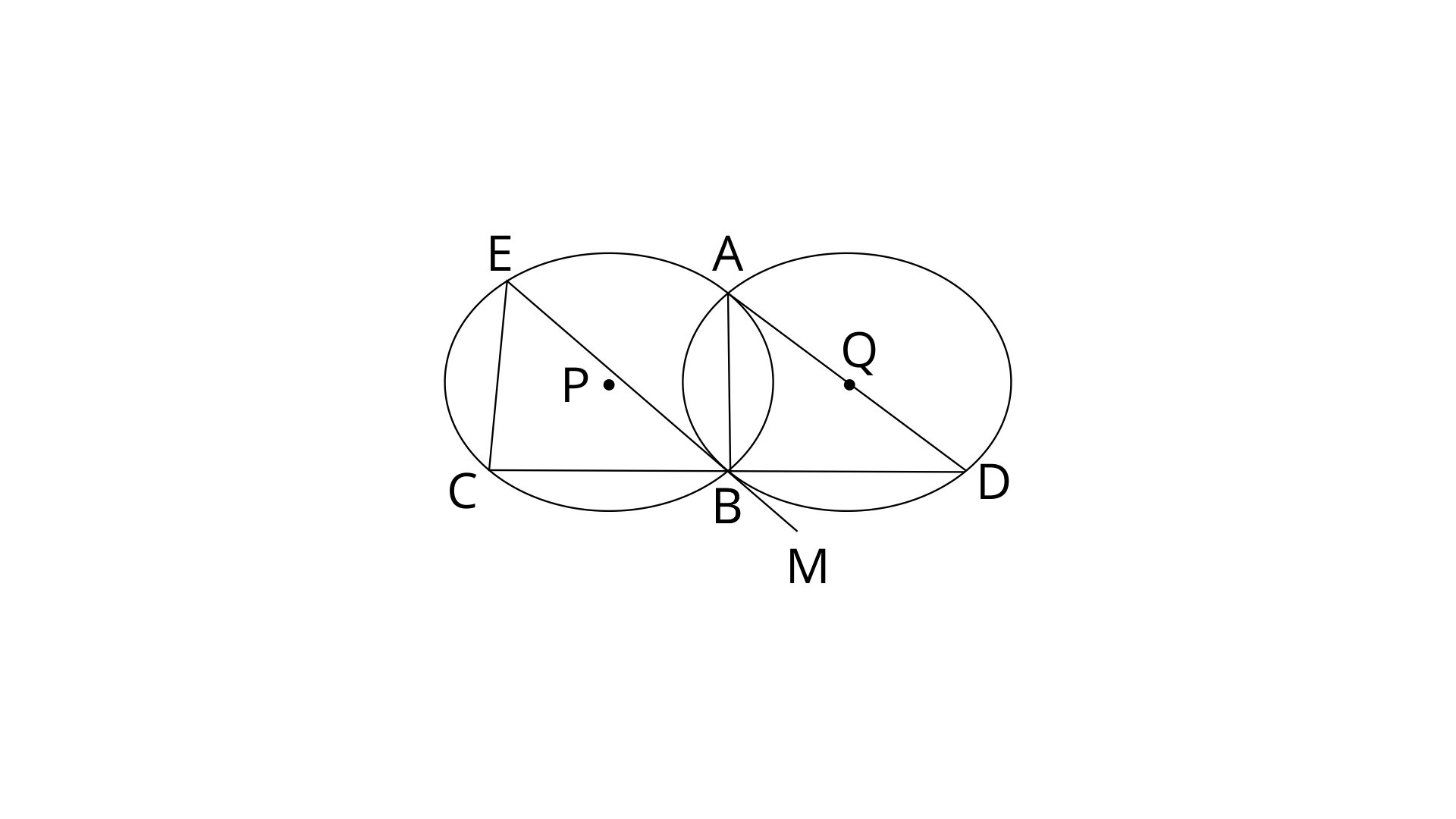
Given that circles are congruent. Therefore the radii of circles are equal.
EBM is tangent to the circle having centre O and BD is chord.
From eq. (1) and (2)
CE=BD (opposite sides of equal angles are equal)
Therefore, CE=BD (Hence proved)
16. In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B.
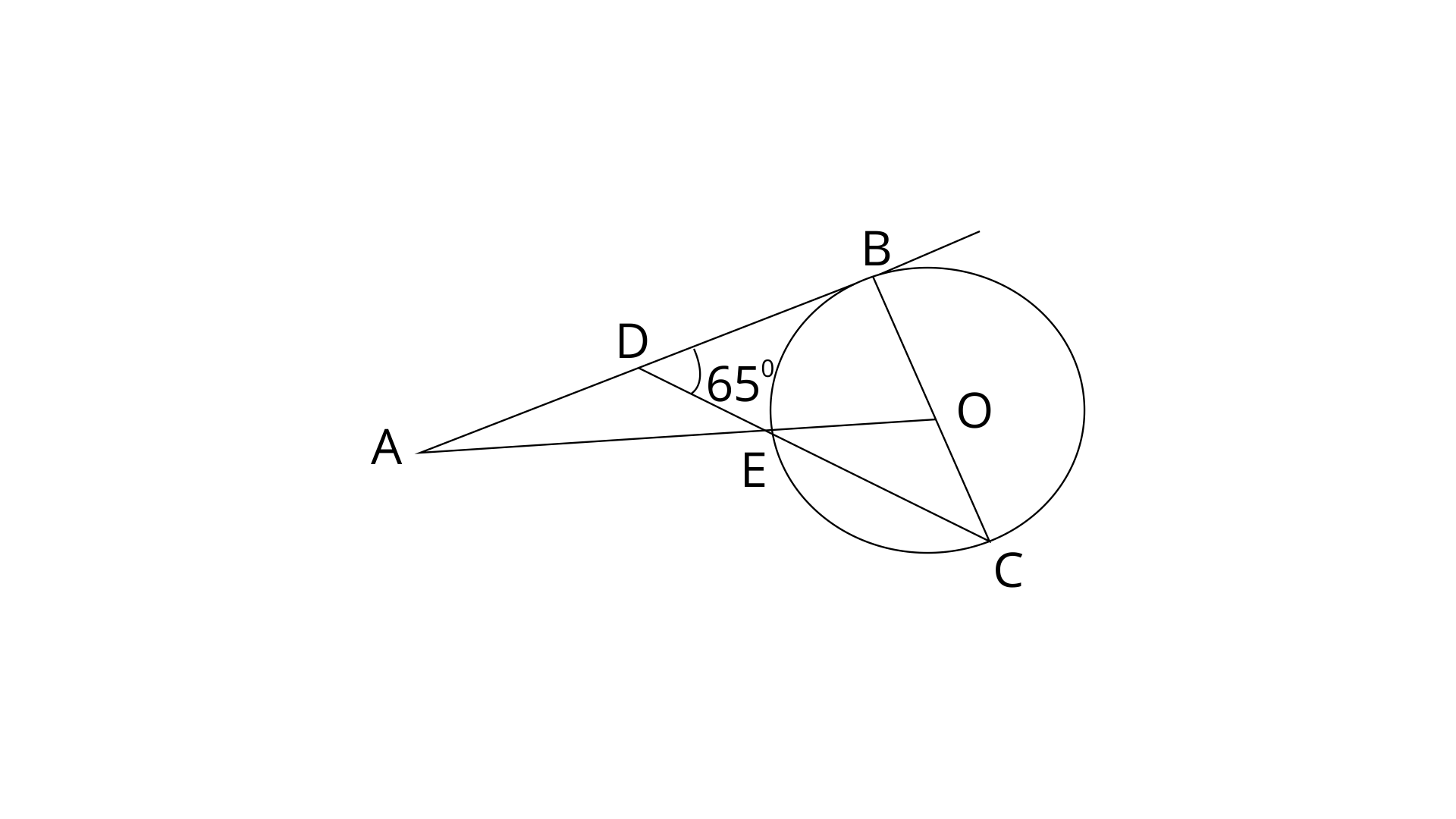
Ans: AB is a straight line and tangent to the circle.
DB is tangent and OB is radius. Radius is perpendicular to the tangent.
By using angle sum property in
OE=OC (radii of same circle)
By using angle sum property in
Therefore,
Thus the value of
EXERCISE-18(C)
1. Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Ans:
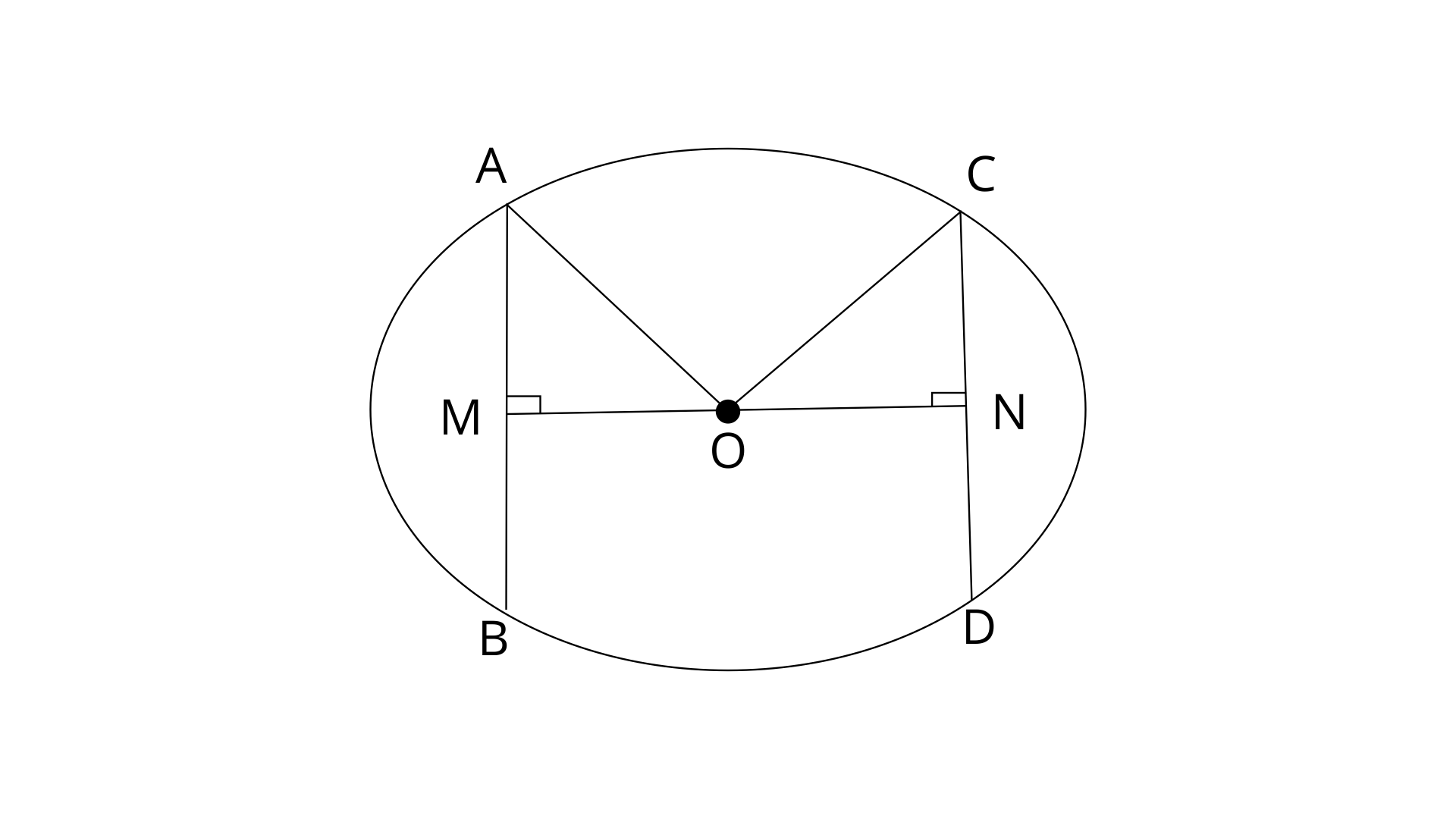
The circle has radius r and AB, CD are chords.
Then we have to prove OM<ON
By using pythagoras theorem in
Similarly in
From eq. (1) and (2)
Given,
Therefore,
Hence chord AB is nearer to the centre than CD.
2. OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O.
(i). If the radius of the circle is 10cm, find the area of the rhombus.
(ii). If the area of rhombus is
Ans:
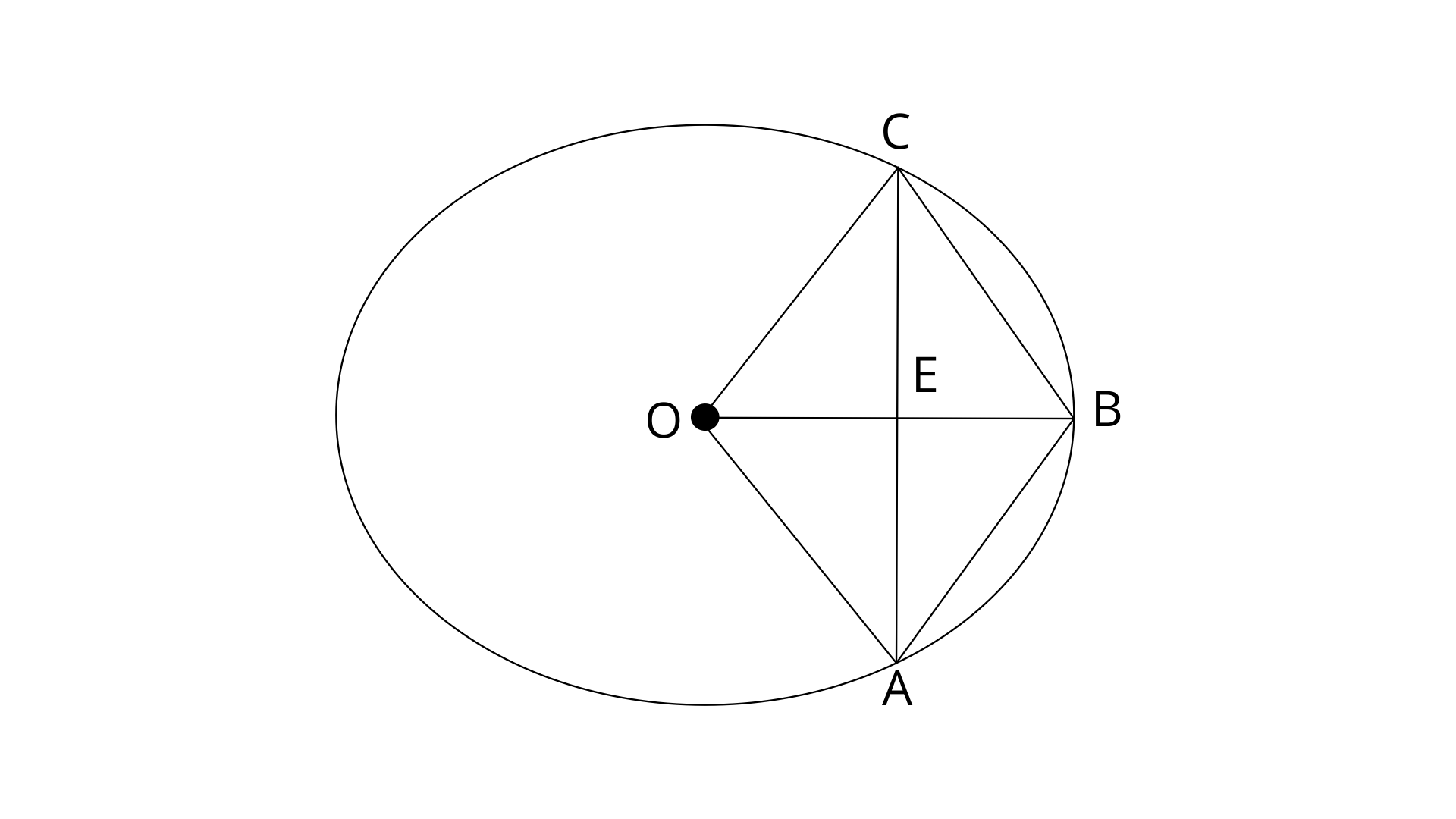
(i). If the radius of the circle is 10cm, find the area of the rhombus.
Ans:
Radius=10cm
In rhombus OABC,
OB=OC=OA=10cm
In a rhombus diagonal are perpendicular and bisect each other.
Therefore,
On using pythagoras theorem in
Now,
Area of rhombus=
Therefore the area of rhombus is
(ii). If the area of rhombus is
Ans: Area of rhombus is
The area of rhombus =
The area of rhombus=
Therefore the radius of the rhombus is 8cm.
3. Two circles with centres A and B, and radii 5cm and 3cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
Ans:
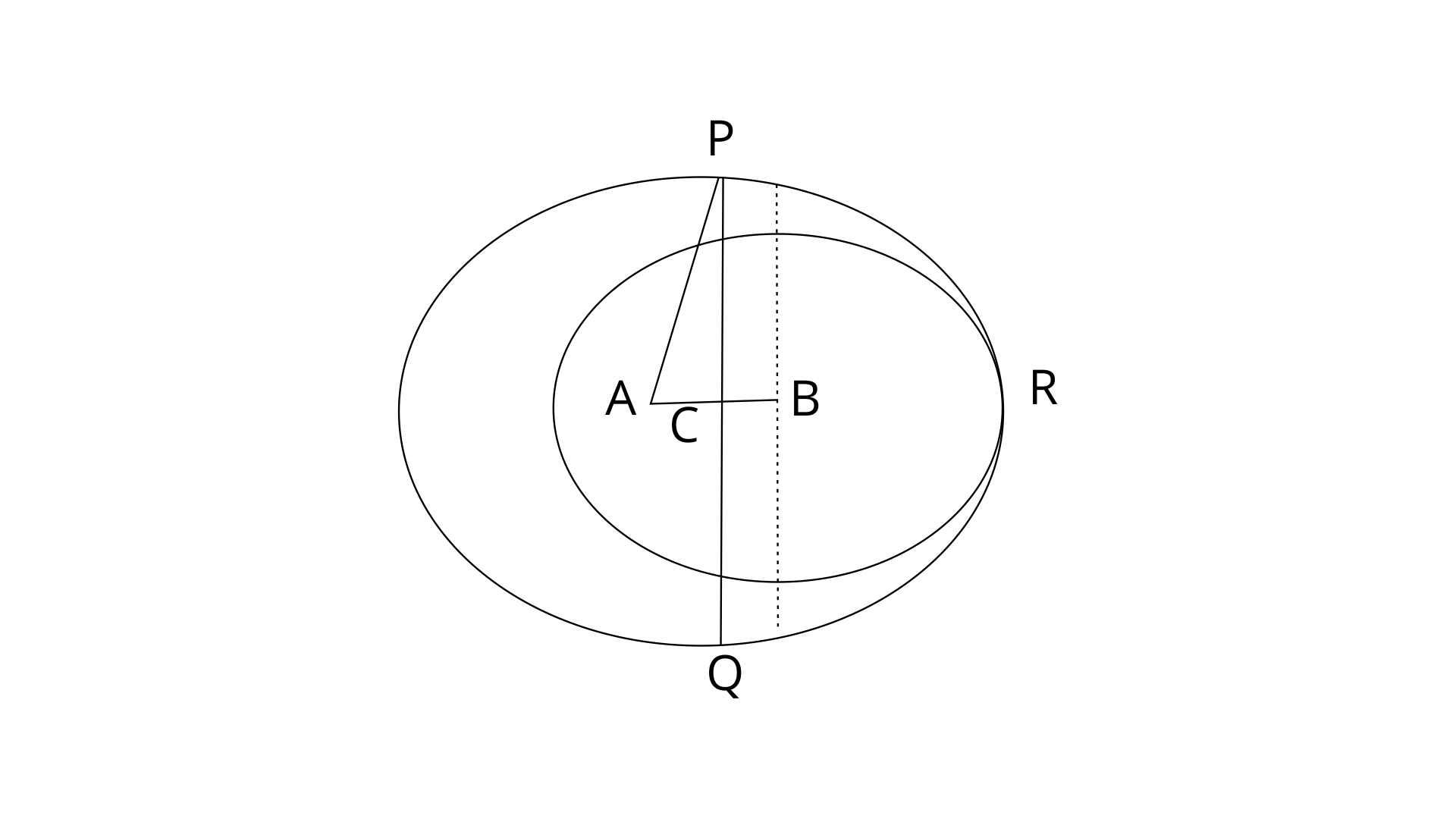
If circles touch internally then the distance between their centres is equal to the difference of their radii.
So, AB=(5-3)=2cm
Given, the common chord PQ is perpendicular to the bisector of AB.
Therefore,
By using pythagoras theorem in
Now,
Therefore the length of
4. Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the circle of angle BAC.
Show that the bisector of angle BAC is a perpendicular bisector of chord BC.
Ans:
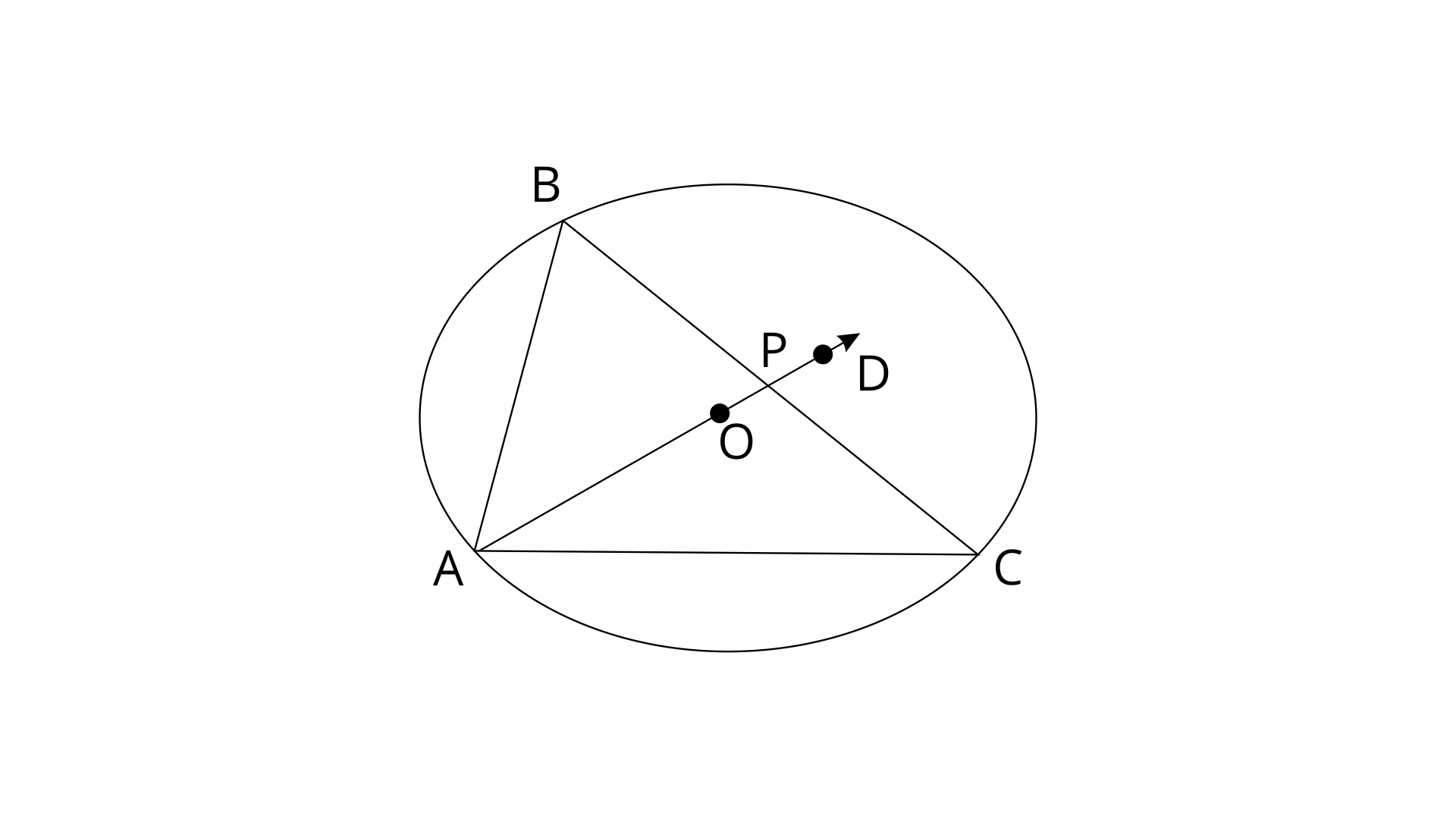
In
AB=AC (Given)
AP=AP (common sides)
Therefore, BP=PC and
Since BP=CP and
Therefore the angle bisector of BAC is perpendicular to BC.
5. The diameter and a chord of a circle have a common end-point. If the length of the diameter is 20cm and the length of the chord is 12cm, how far is the chord from the centre of the circle ?
Ans:
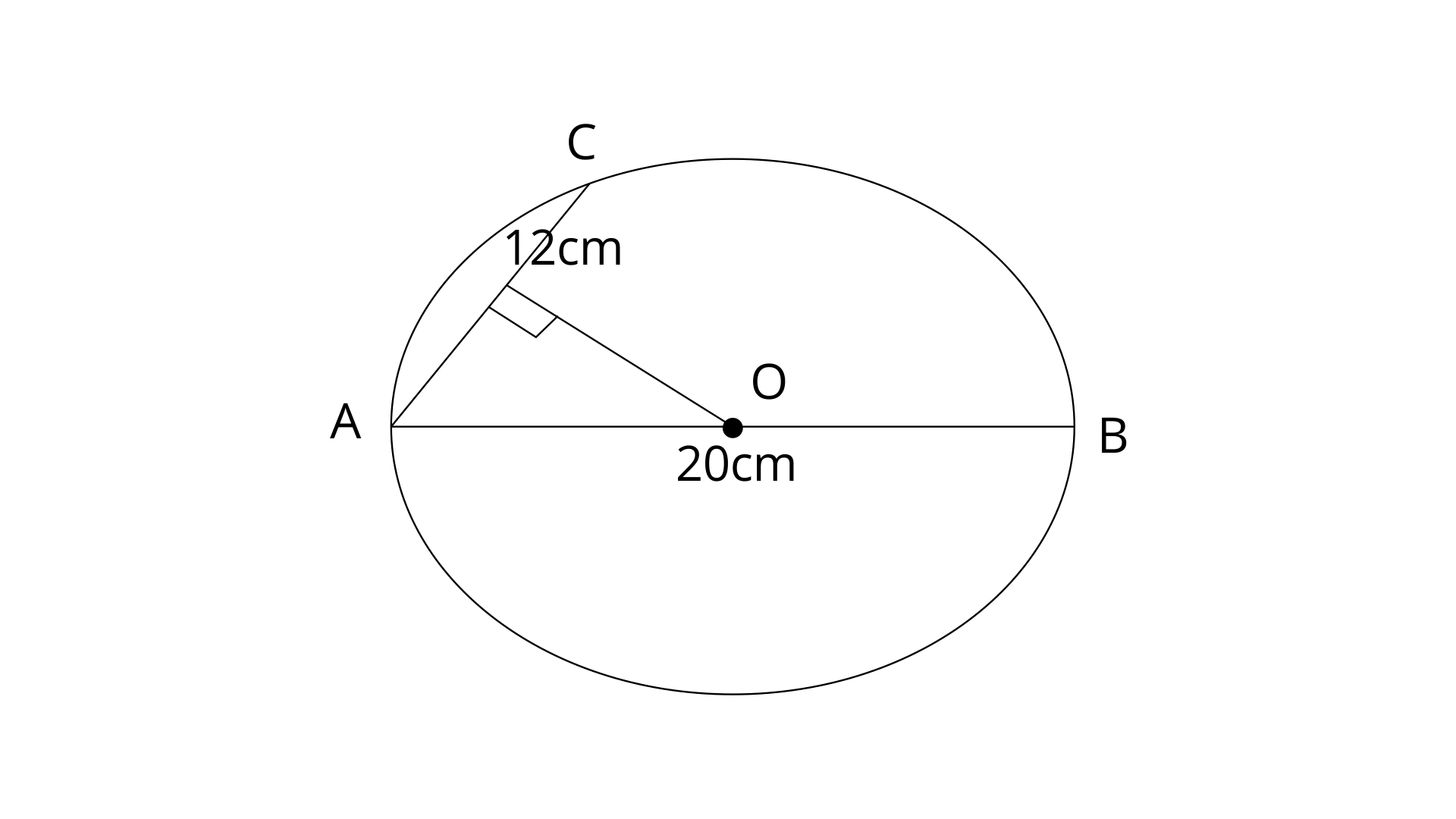
AB is diameter and AC is a chord. A is the common point of chord and diameter.
Draw
The perpendicular on a chord drawn from the centre bisects the chord.
Therefore, AL=LC=
Now by using pythagoras theorem in
Therefore the chord is at a distance of 8cm from the centre of the circle.
6. ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle
Ans:
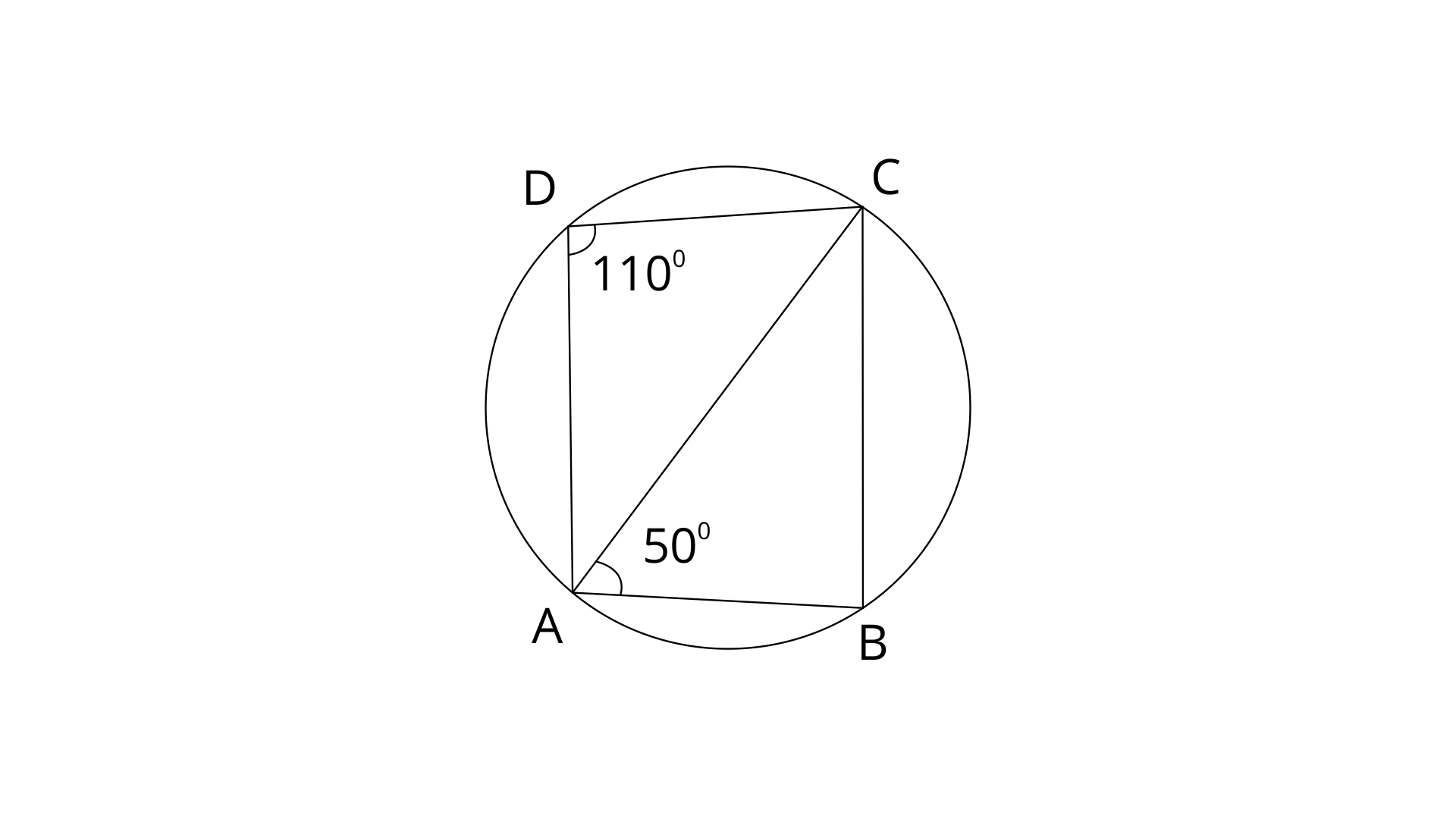
ABCD is a cyclic quadrilateral.
Therefore,
By using angle sum property in
Since, AD||BC
Therefore,
Thus the value of
By using angle sum property in
Thus the value of
7. In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle
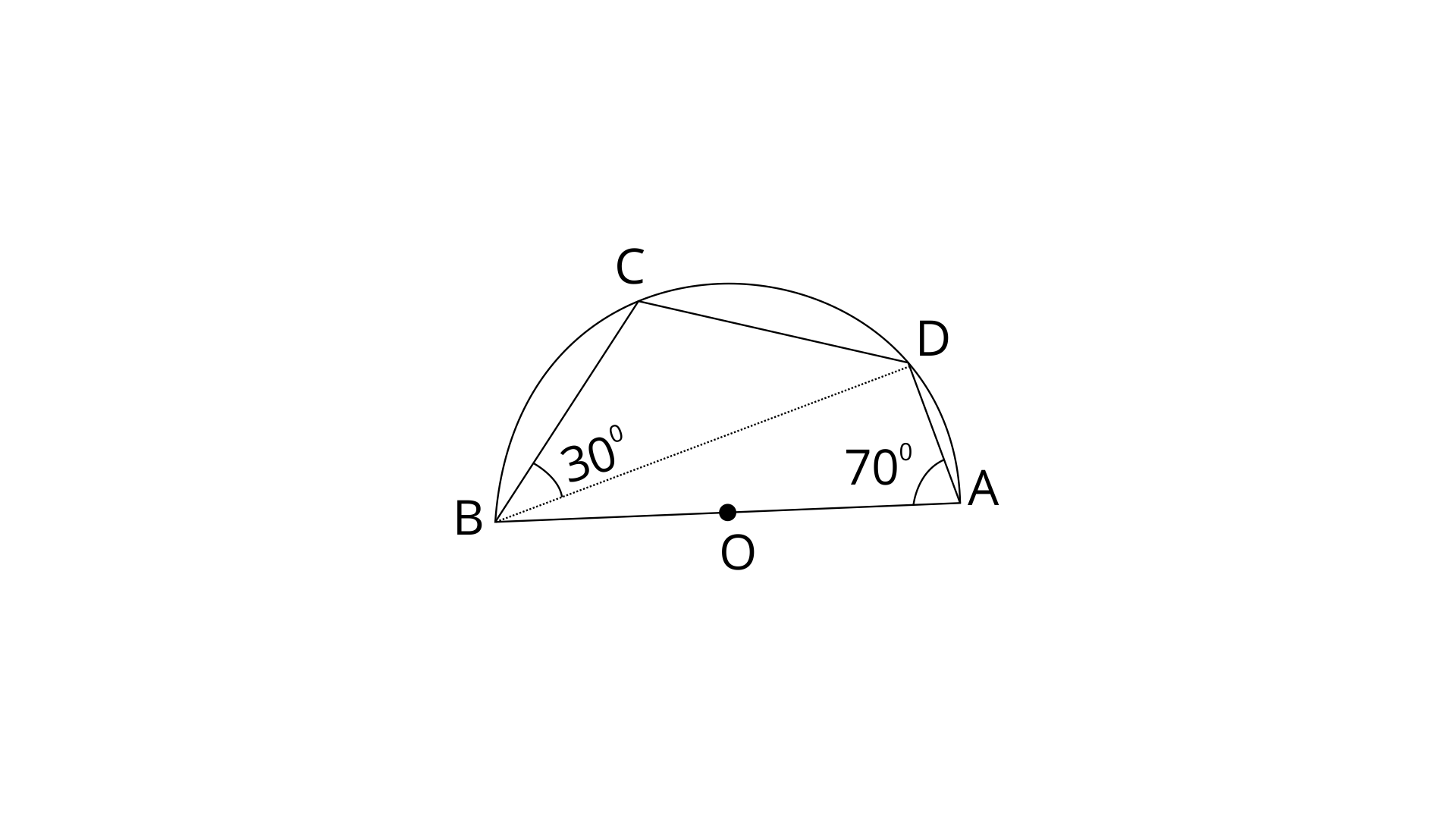
Ans: ABCD is a cyclic quadrilateral. In a cyclic quadrilateral the sum of opposite angles is
By using angle sum property in
Thus the value of
8. In a cyclic quadrilateral ABCD,
Ans:
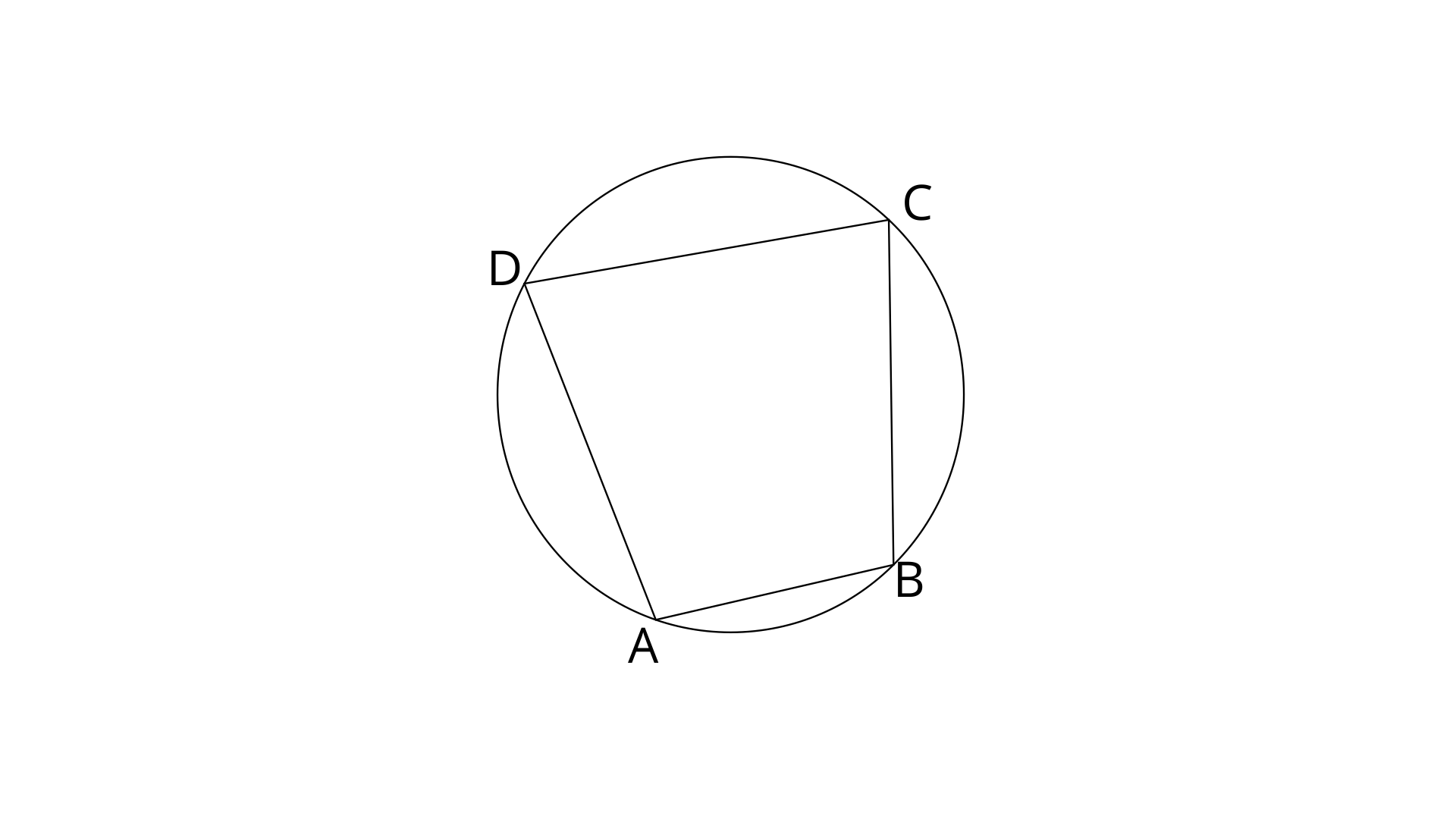
ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is
Therefore,
Similarly,
Thus the value of
9. Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Ans:
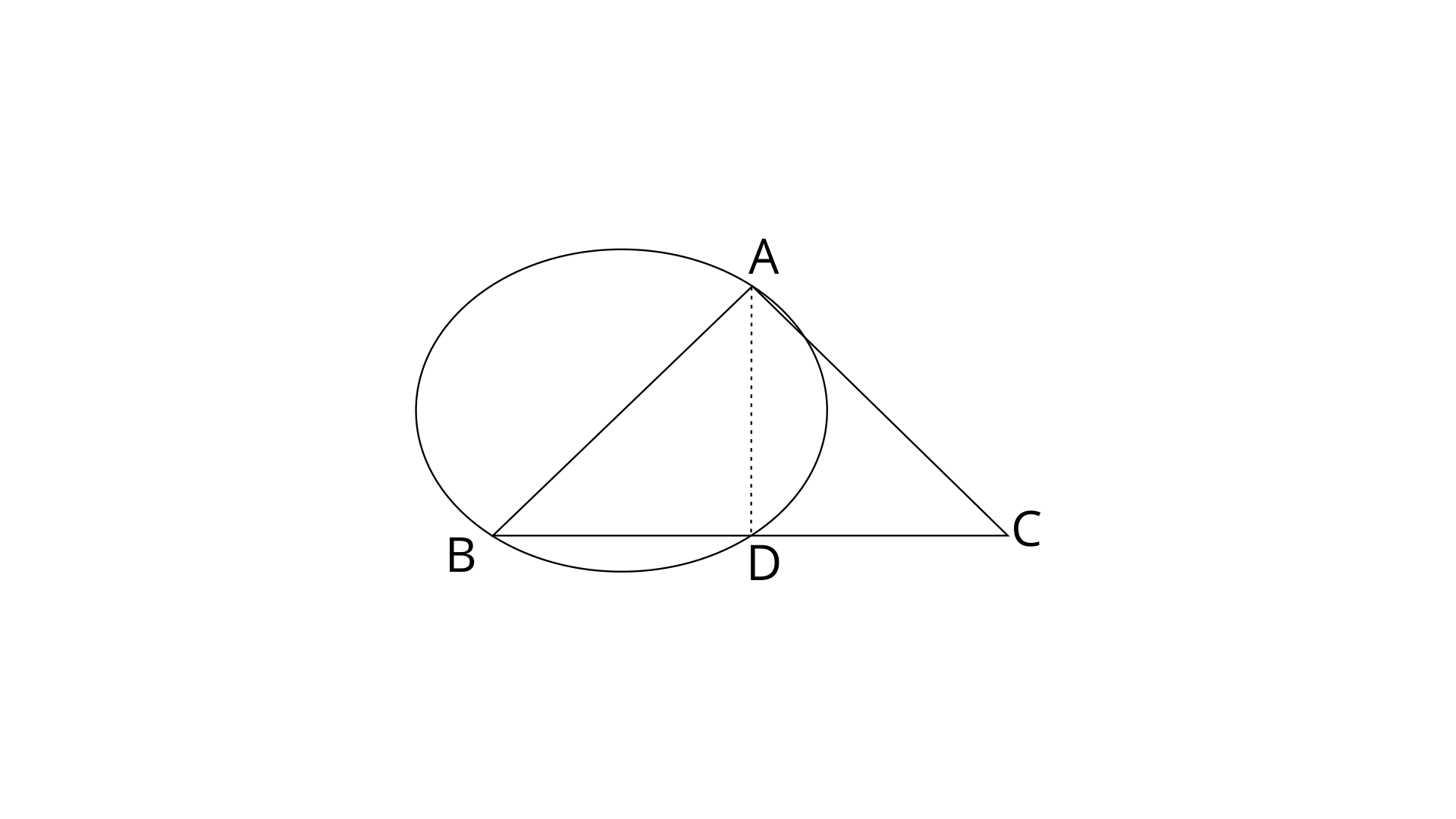
AB is a diameter and
BDC is straight line.
In
AD=AD (common side)
AB=AC (Given)
Therefore, BD=CD (C.P.C.T)
Hence, The circle bisects the base BC at D.
10. Bisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the point D, E and F respectively. Prove that angle
Ans:
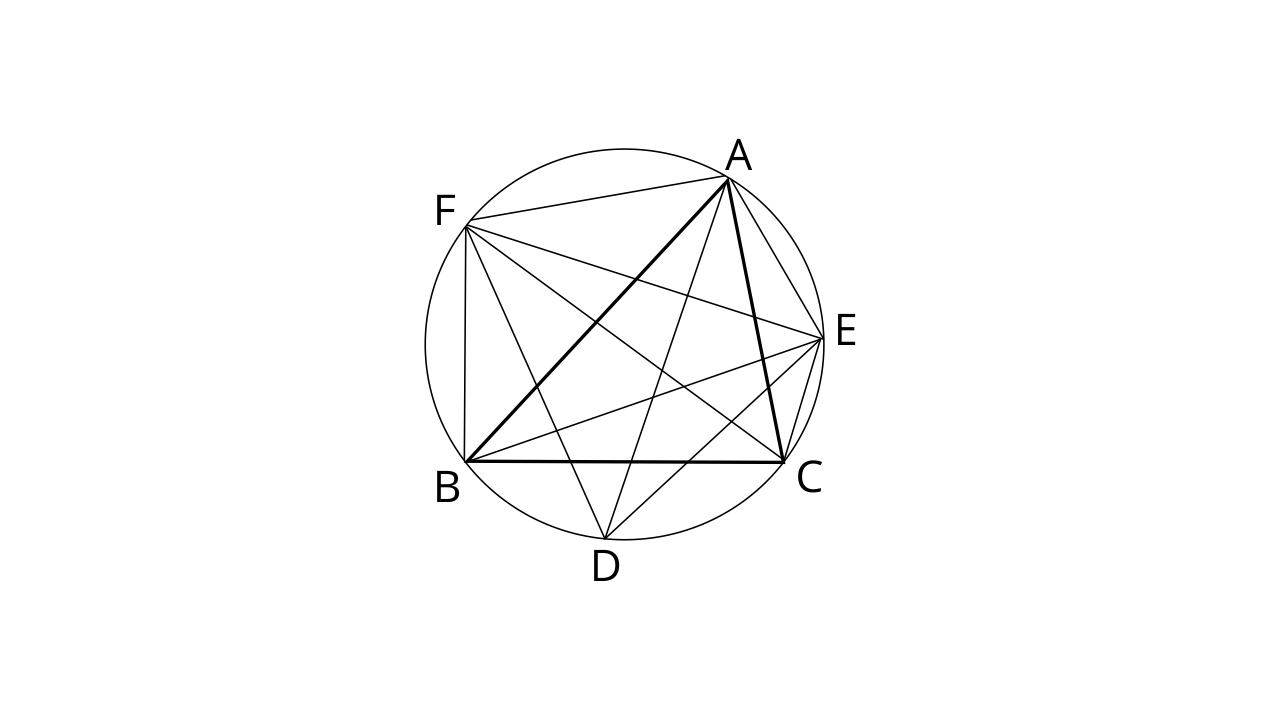
AD, BE and CF are angle bisectors of
Therefore,
Similarly,
Sum of all interior angle in a triangle is
Now substituting the above value in eq. (1)
11. In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC=DO. If
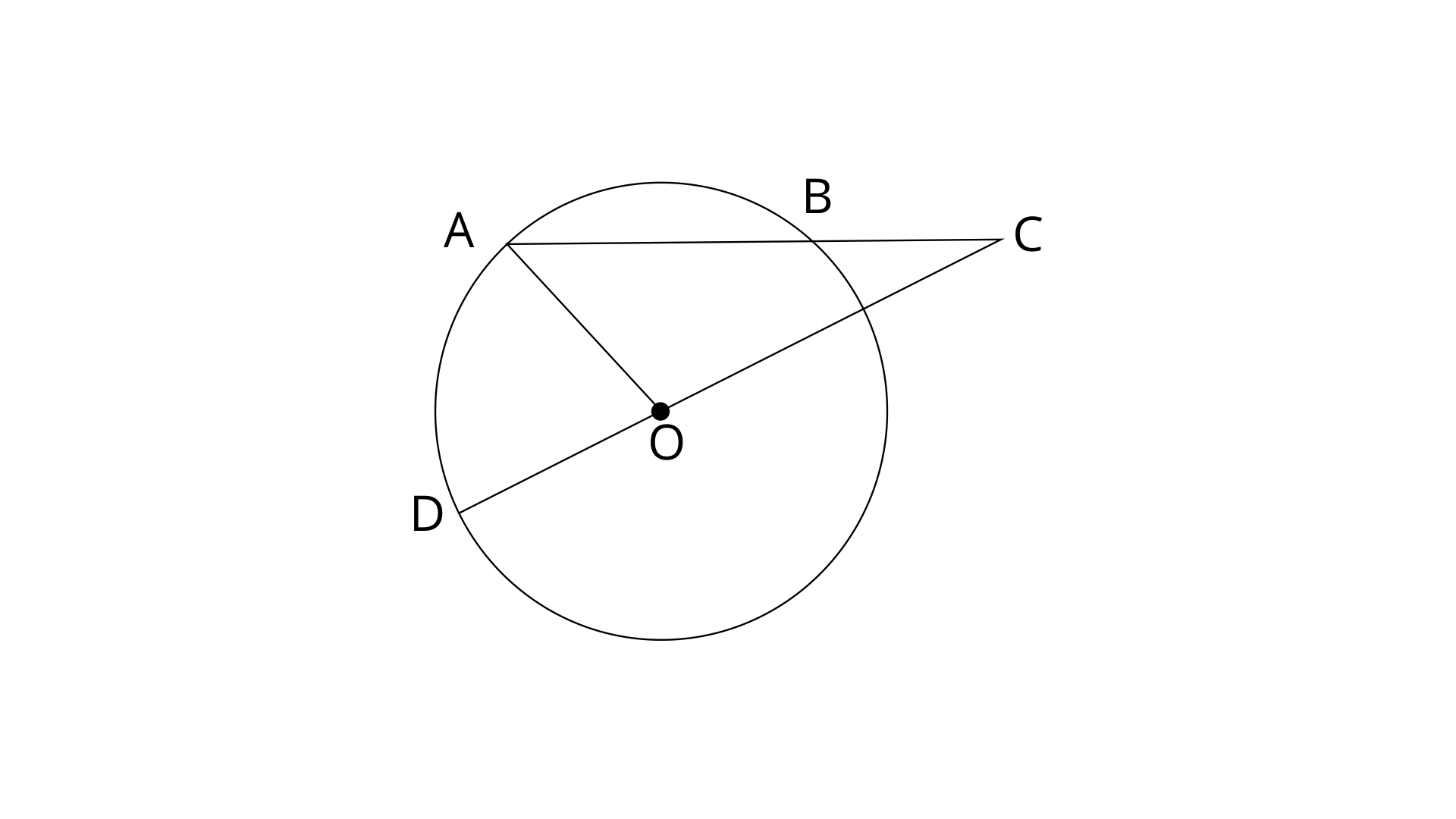
Ans: Join OB

BC=OD (Given)
OD=OA=OB (Radii of same circle)
Therefore, OD=OB=BC
In
Since, OA=OB(Radii of same circle)
In
DOC is a straight line,
Thus the value of
12. Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Ans:
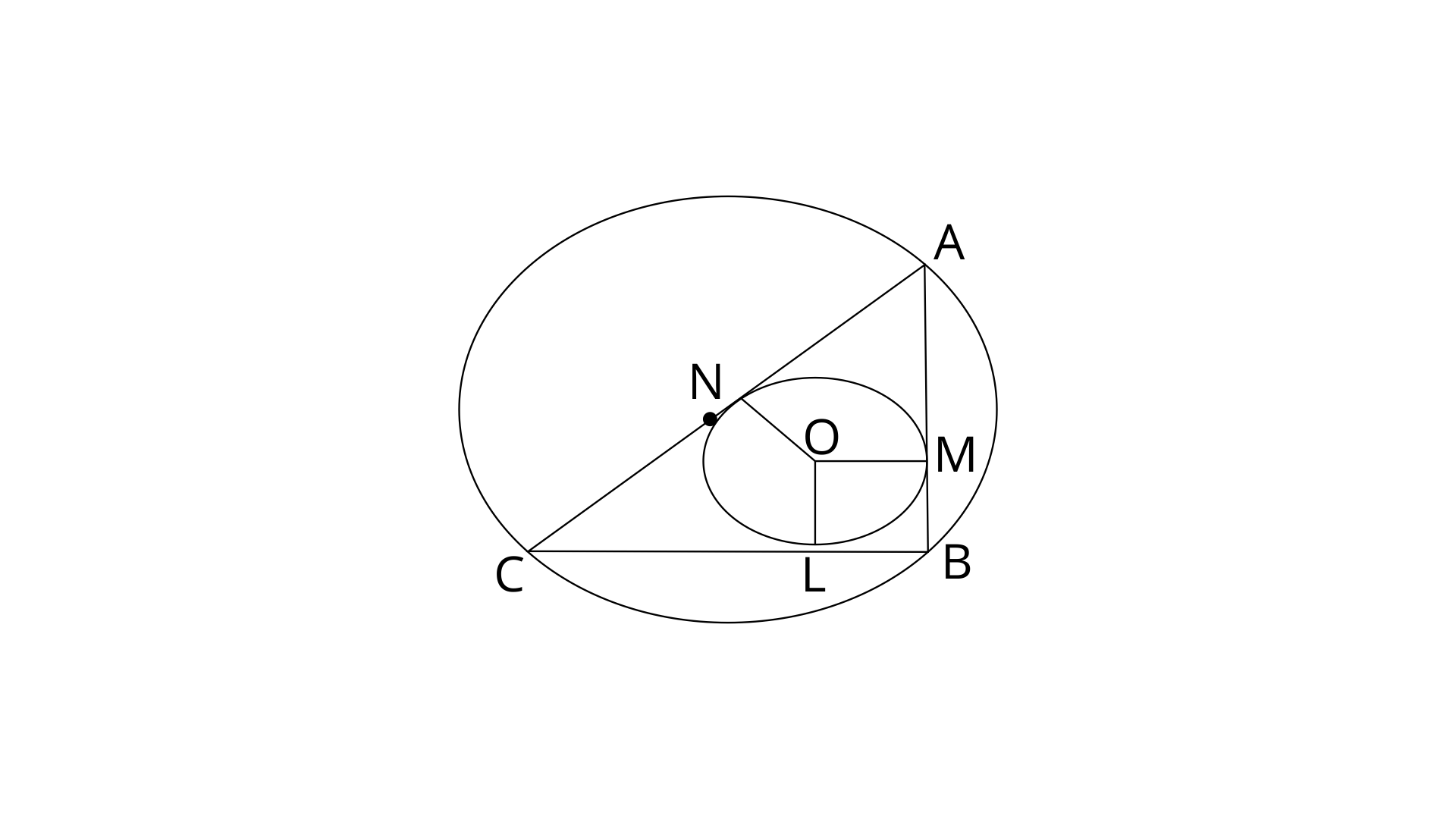
Let D and R the diameter and radius of circumcircle and let d and r the diameter and r the diameter and radius of incircle.
In
AC is the diameter of the circumcircle Therefore, AC=D
And, OL=OM=ON=r
Now, from B, BL and BM are tangents.
BL=BM=r (∵BL=OM)
Similarly, AN=AM=R (Tangents from C) and CL=CN=R (Tangents from C)
Perimeter of triangle is sum of all the sides,
13. P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
Ans:
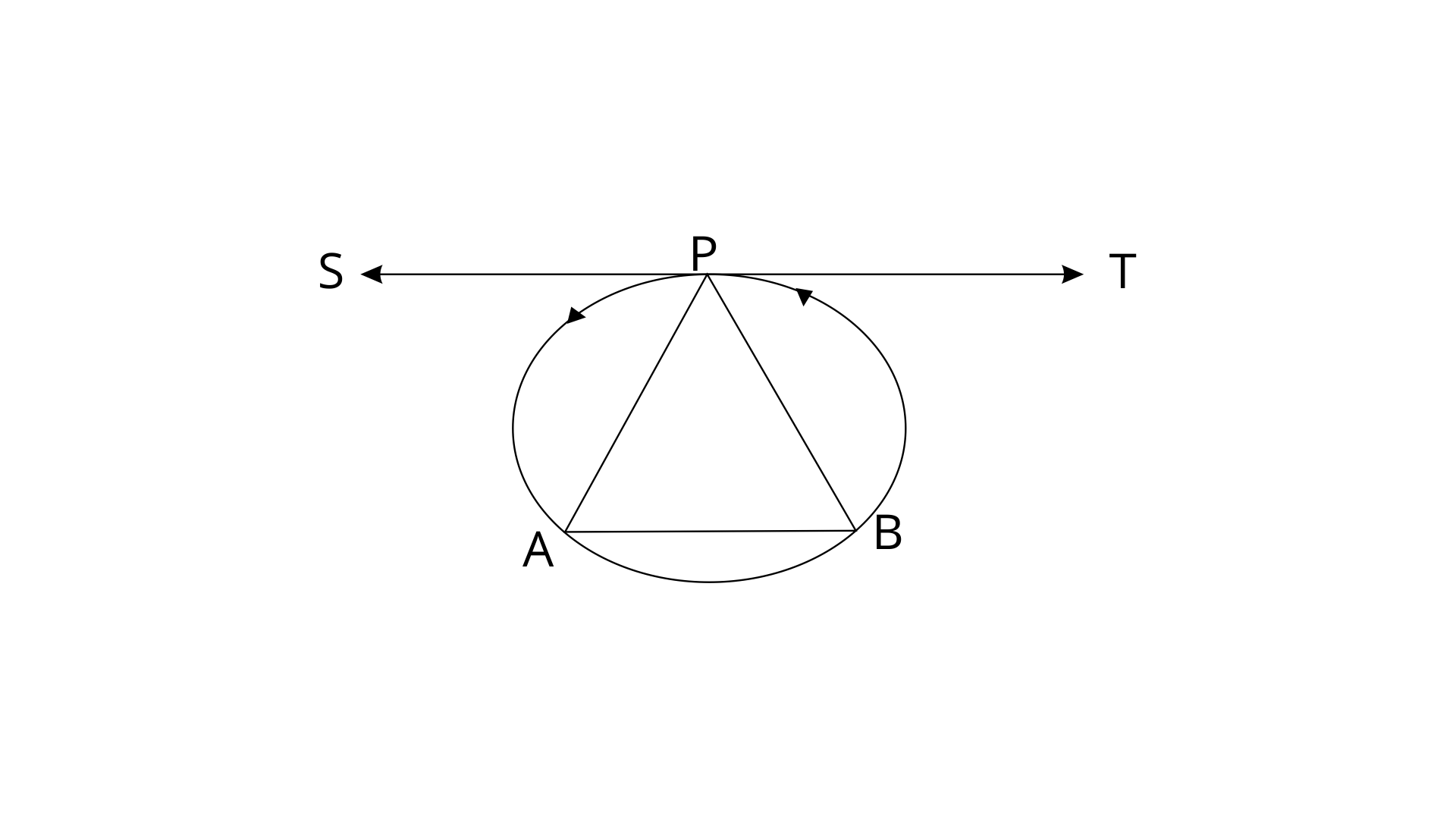
Since TPS is tangent to the circle and PB is chord.
Since P is the midpoint of arc AB. Hence Chord PA=PB
From eq.(1) and (2)
But these are alternate angles.
Therefore, TPS||AB
14. In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
Prove that the line NM produced bisects AB at P.
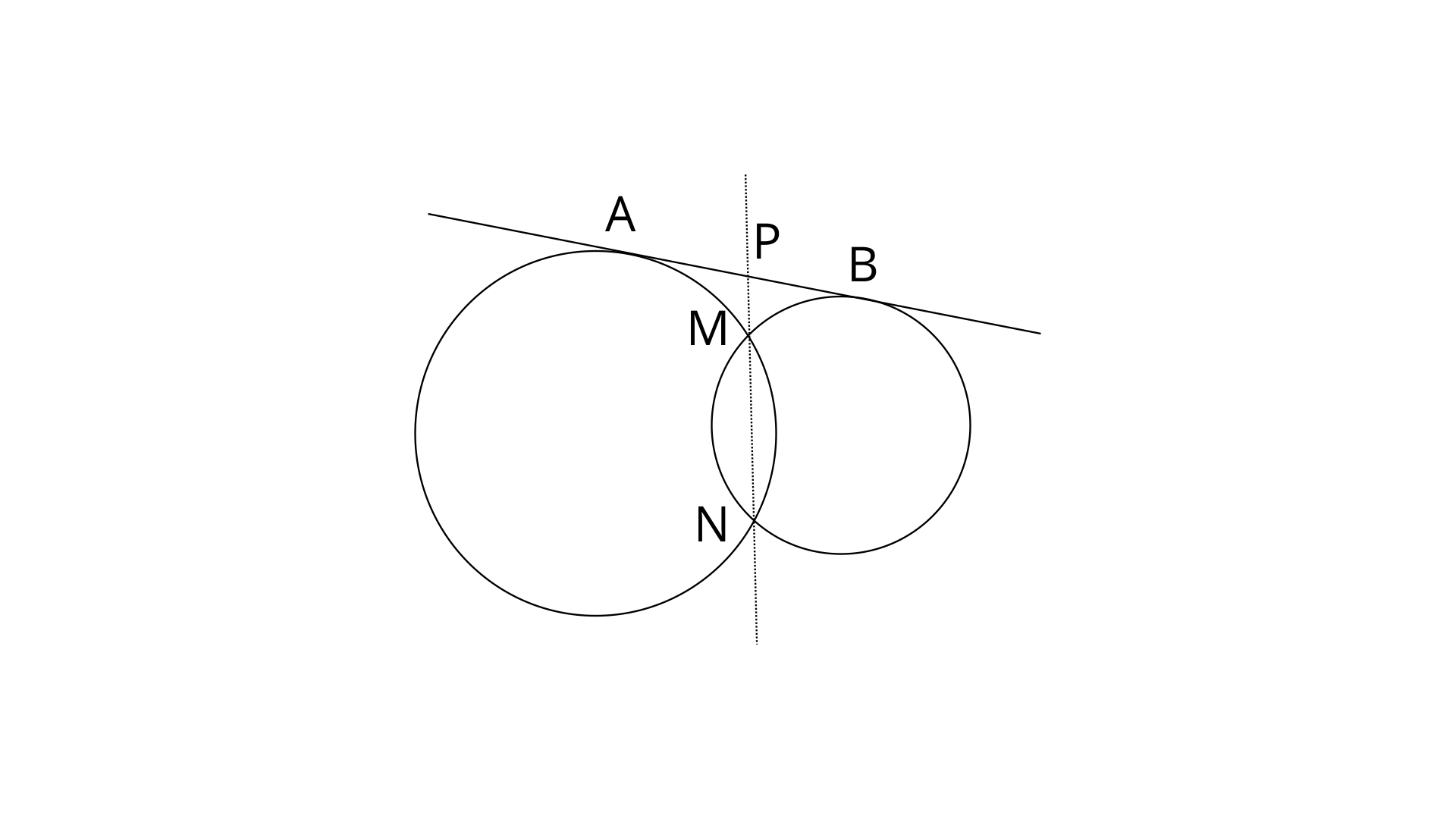
Ans:
AP is a tangent to the circle from the point P and PMN is secant.
Therefore,
Similarly, PB is tangent to the circle from point P and PMN is secant.
Therefore,
From eq.(1) and (2)
Therefore, Line NM produced bisects AB at P.
15. In the given figure, ABCD is a cyclic-quadrilateral, PQ is tangent to the circle at point C and BD is its diameter.
If
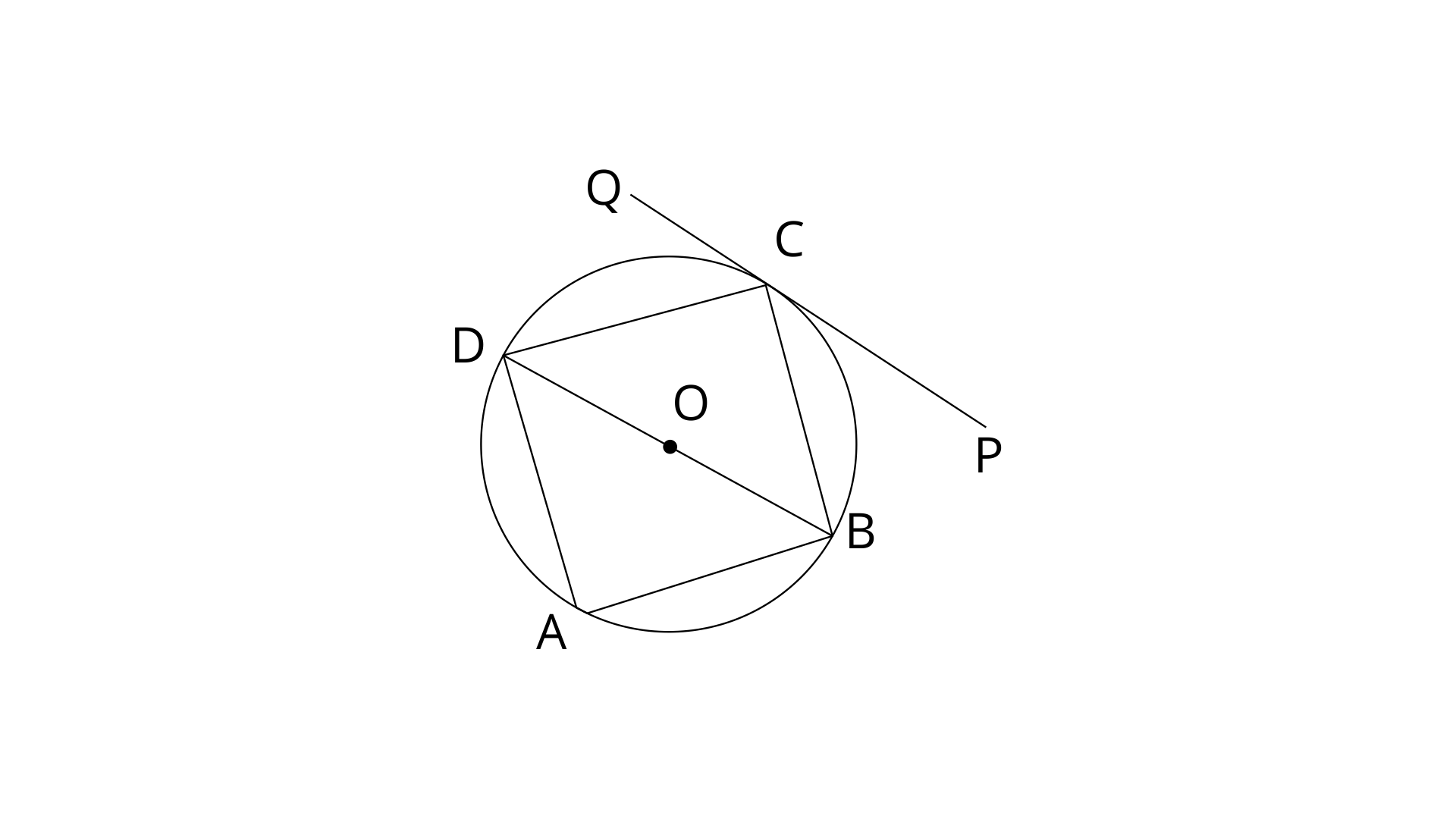
(i)
Ans: PQ is a tangent to the circle and DC is the chord.
Therefore,
∴
(ii).
Ans: Angle
PCQ is straight line.
(iii).
Ans:
By using angle sum property in
Thus the value of
16. The given figure shows a circle with centre O and BCD is tangent to it at C. Show that:
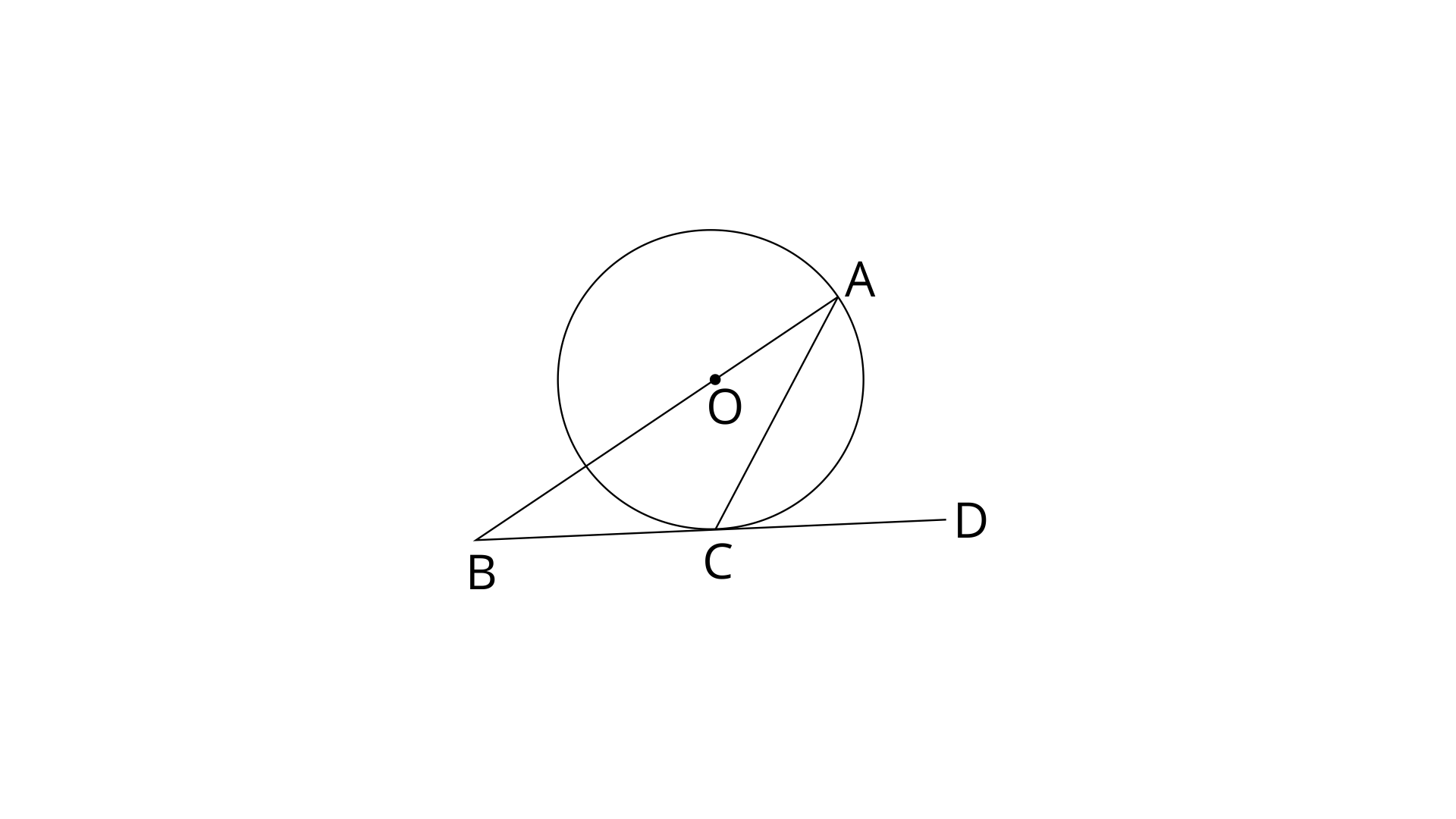
Ans: Join OC.
BCD is a tangent and OC is radius. Radius is perpendicular to the tangent.
Therefore,
In
OC=OA (Radii of same circle)
Therefore,
From eq.(1) and (2)
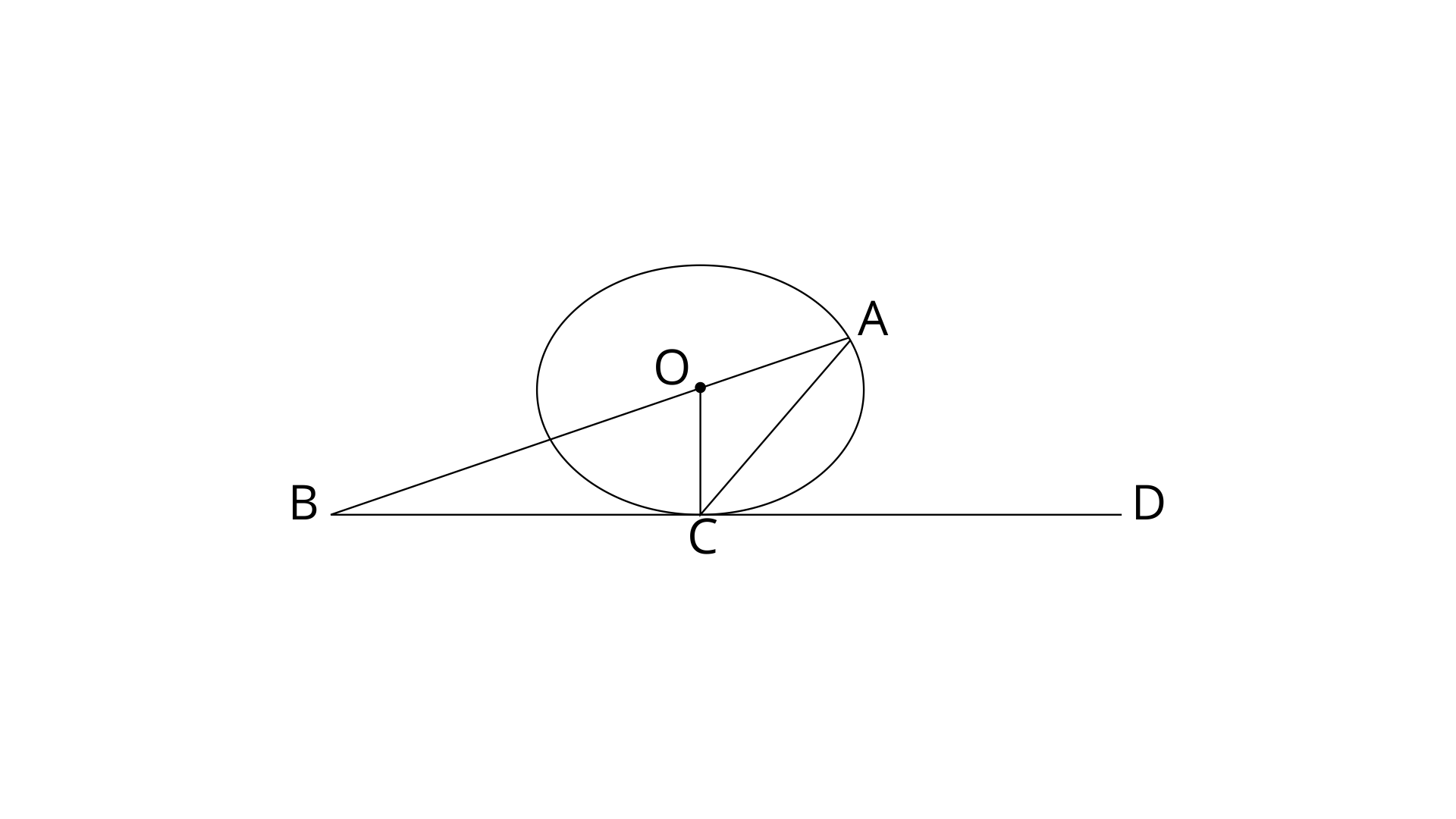
17. ABC is a right triangle with angle
(i).
Ans:
In
Therefore, AB is tangent.
AB is tangent and ADC is secant.
Therefore,
(ii).
Ans: In
By using exterior angle property,
Now, In
Since
Therefore,
From eq. (1) and (2)
Now in
BD=BD (common side)
Therefore,
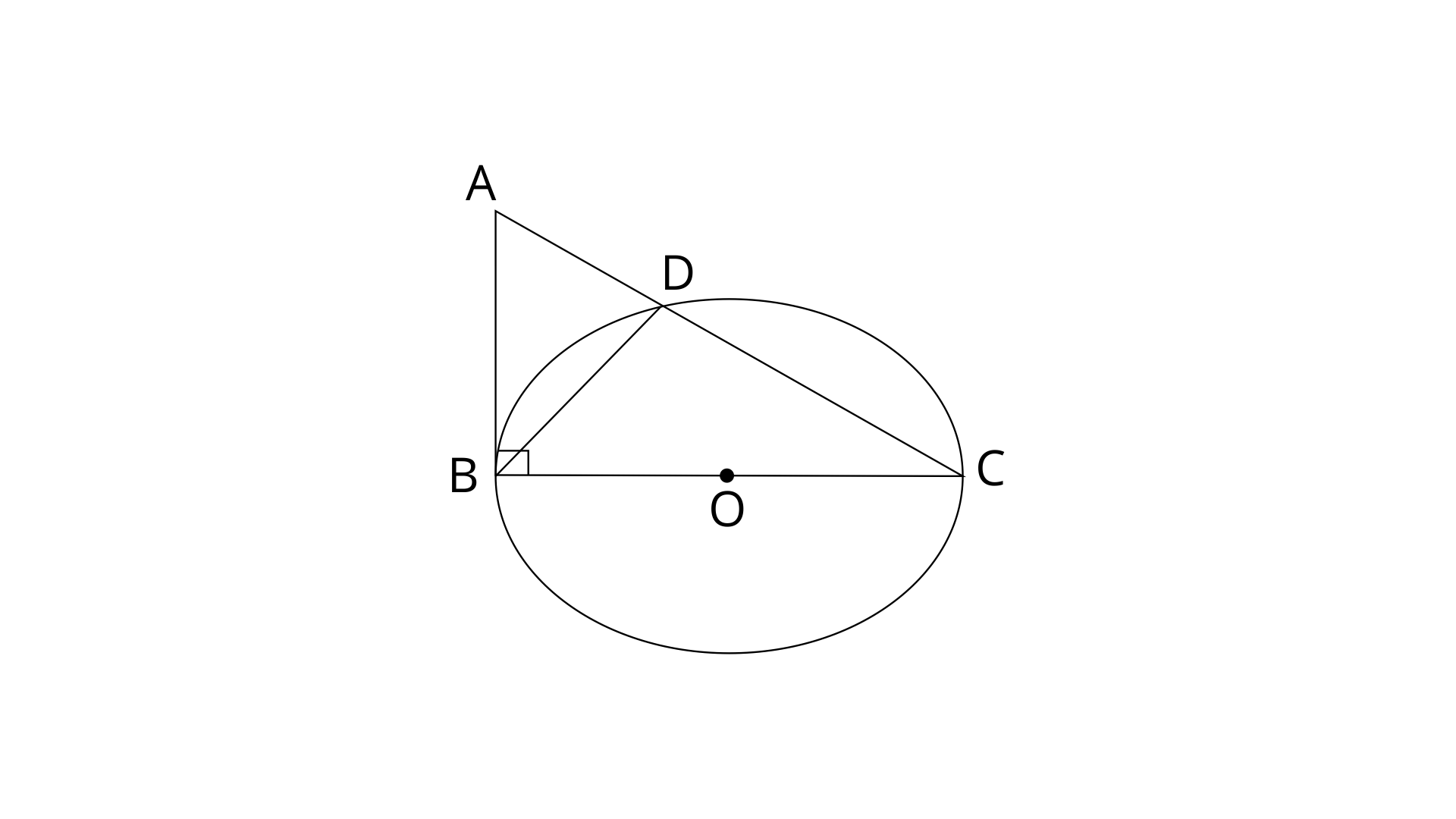
18. In the given figure, AC=AE. Show that :
(i).
Ans: In
AC=AE (Given)
∴
Therefore, AB=AD
But AC=AE
In
BC=DE
Therefore, CP=EP (C.P.C.T)
(ii).
Ans: Since,
Therefore,
19. ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB=BC=CD and angle
(i).
Ans:
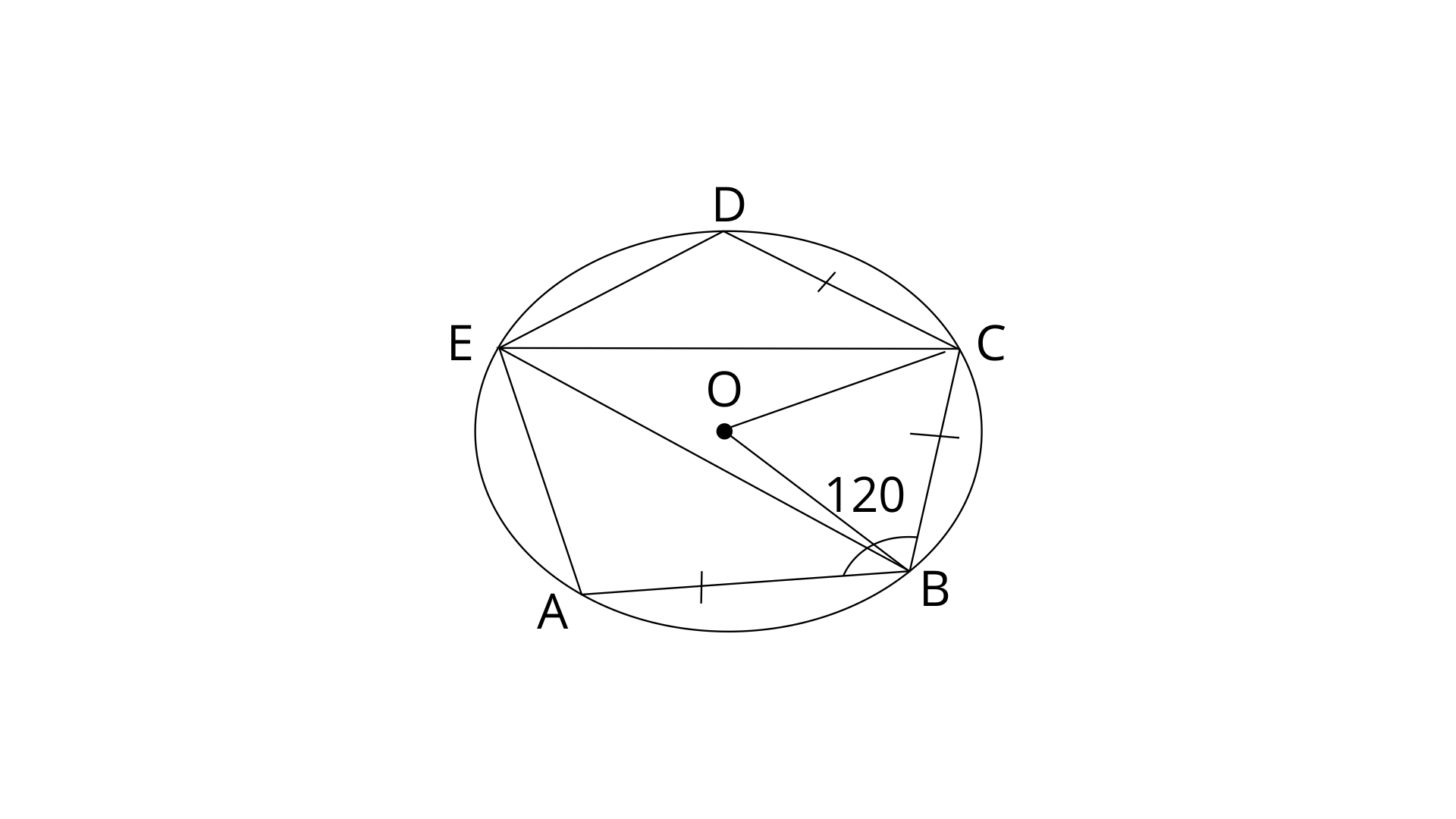
Given, AB=BC=CD and
Therefore,
OB and OC are the bisectors of
In
In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
Therefore,
(ii).
Ans: BCDE is cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is
Thus the value of
20. In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If
(i).
(ii).
(iii).
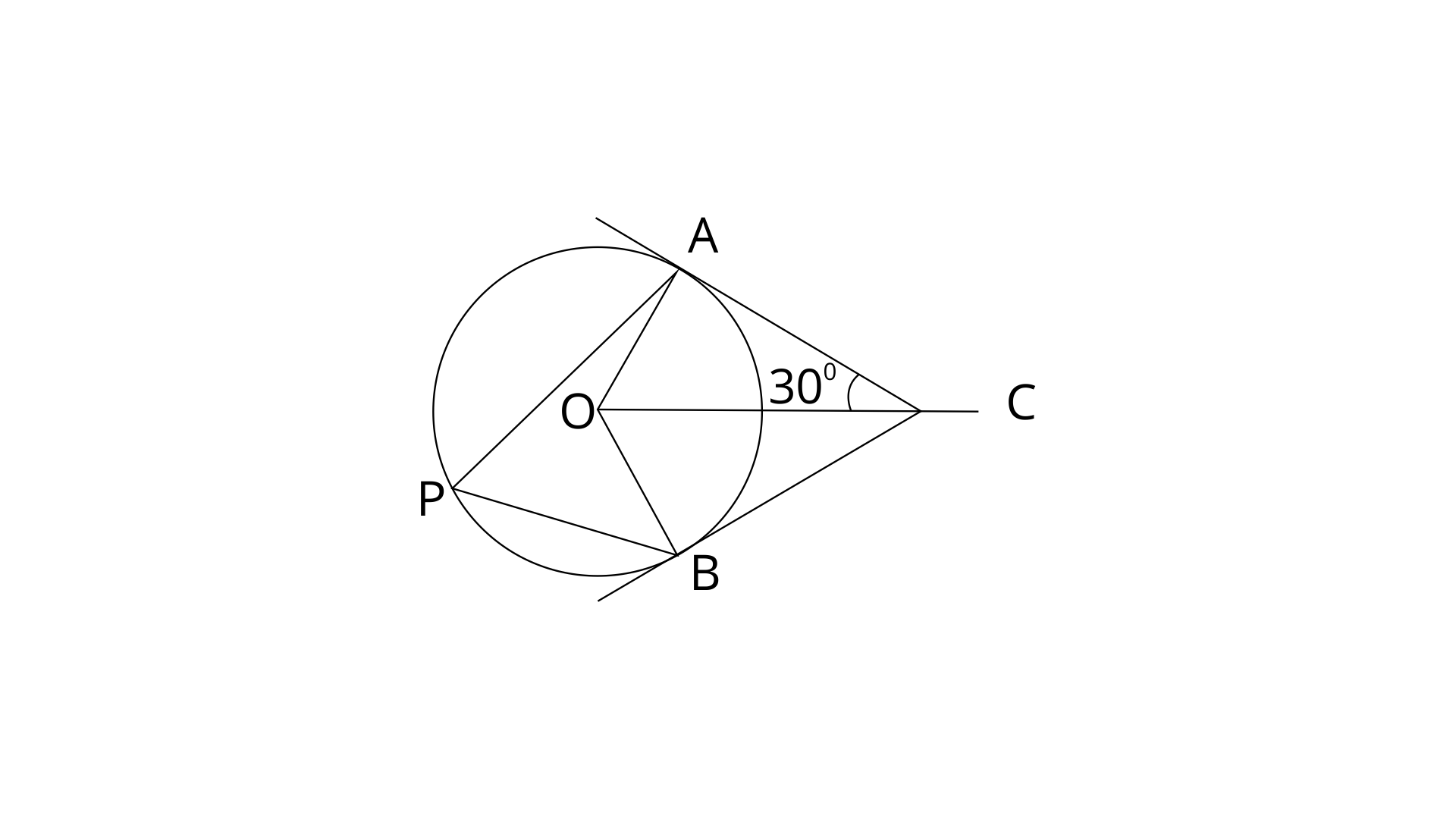
(i).
Ans: In
OC=OC (common side)
OA=OB (Radii of same circle)
AC=BC (Tangents to the circle from external point C)
Therefore,
(ii).
Ans:
Sum of opposite angles in quadrilateral is
(iii).
Ans: In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
21. ABC is a triangle with AB=10cm, BC=8cm and AC=6cm (not drawn to scale). There circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
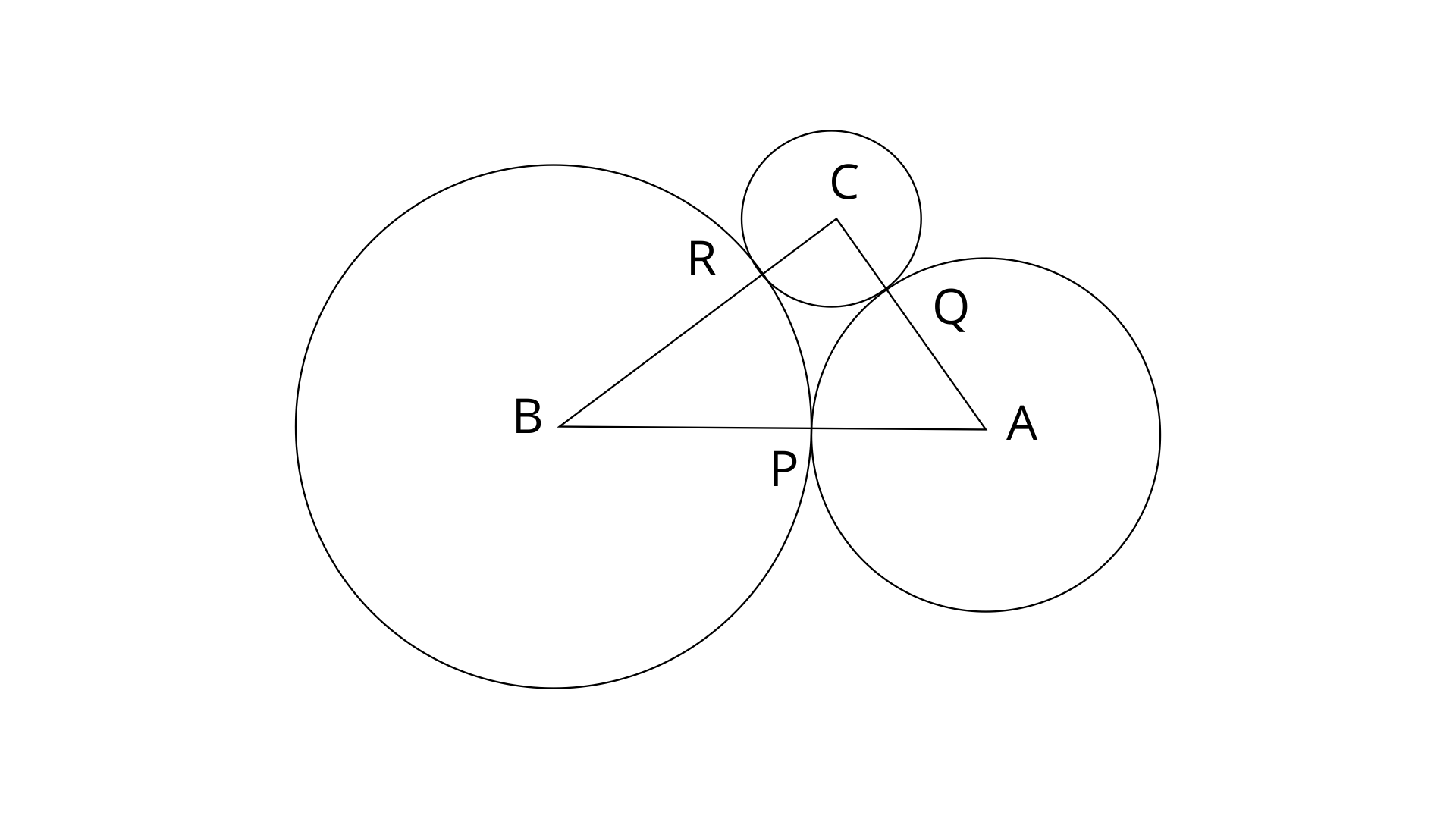
Ans: Given,
Let PA=QA=x (Radii of circle having centre A)
CR=CQ=y (Radii of circle having centre C)
BP=BR=z (Radii of circle having centre B)
On adding eq. (1), (2) and (3)
Subtracting eq.(1) from (4)
Subtracting eq.(2) from eq.(4)
Subtracting eq.(3) from eq.(4)
Therefore the radii of circles are 2cm, 4cm and 6cm.
22. In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that :
(i).
Ans:
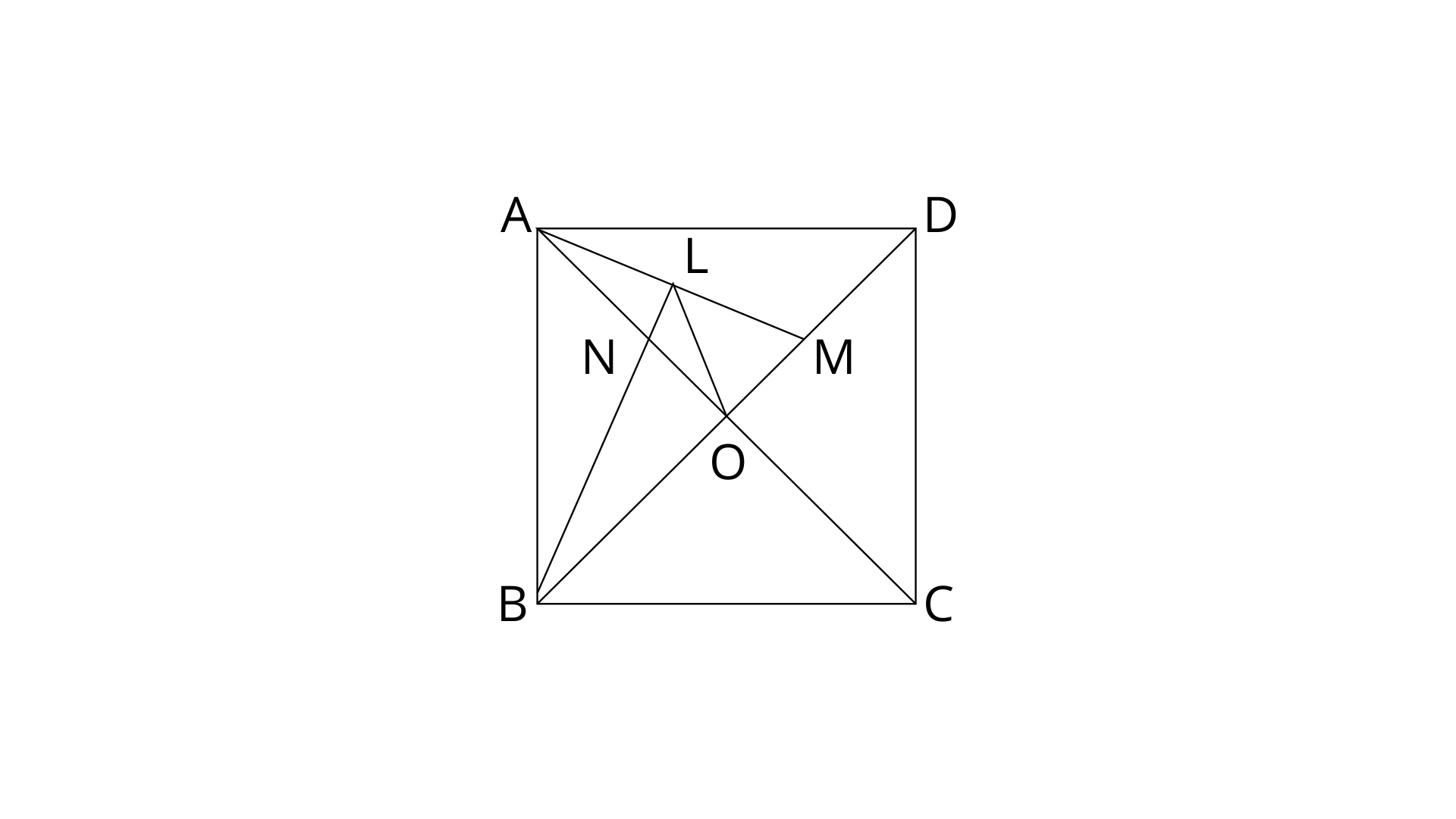
ABCD is a square. Hence, All four angles are right angle and diagonals are also intersect at
In
Since,
Therefore,
Again, In
On adding eq. (1) and (2)
Since,
Therefore,
(ii).
Ans:
By using angle sum property in
Since,
Therefore,
(iii). ALOB is a cyclic quadrilateral.
Ans:
23. The given figure shows a semi-circle with centre O and diameter PQ. If PA=AB and
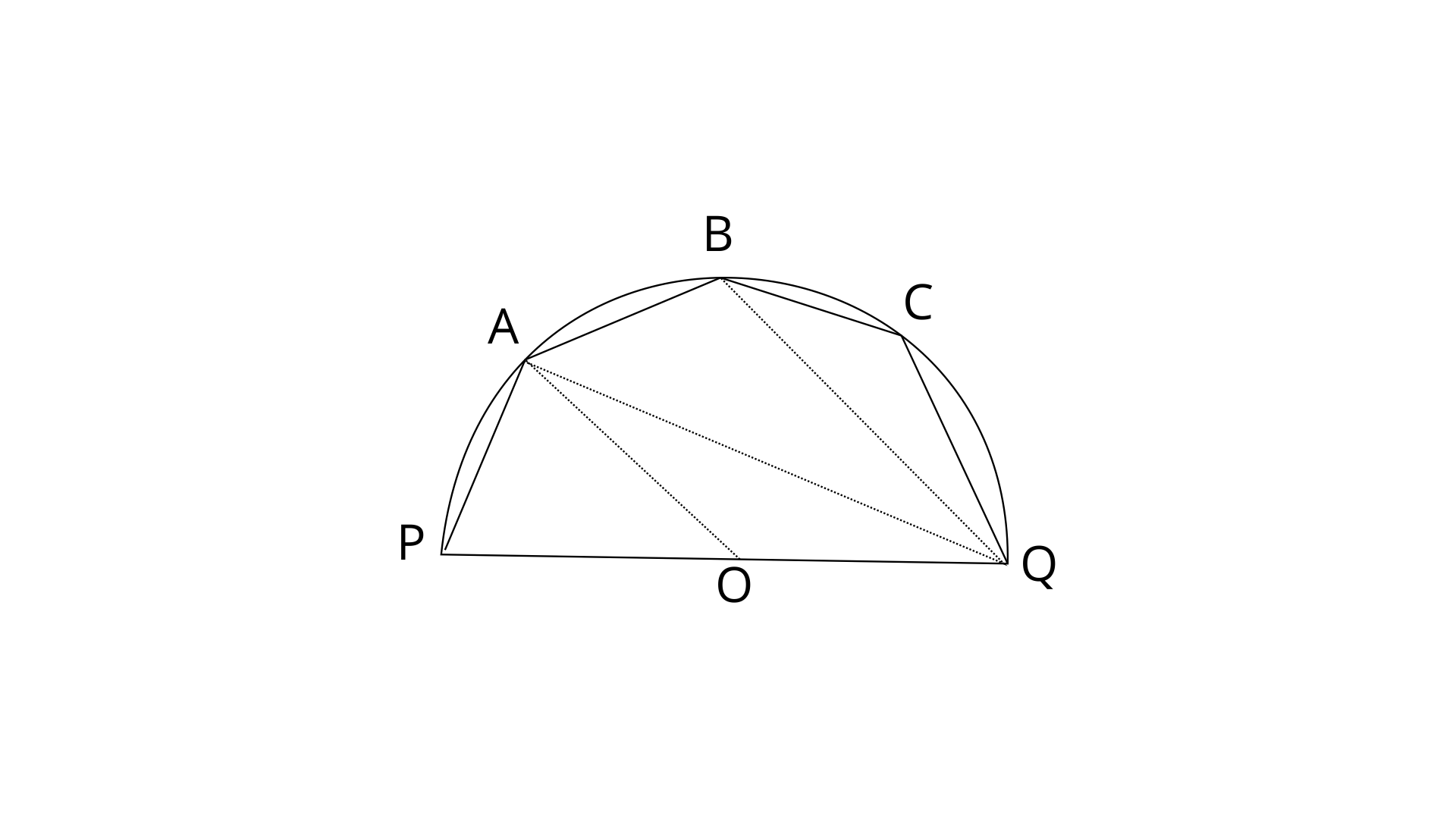
Ans: Join PB.

In cyclic quadrilateral PBCQ,
By using angle sum property in
In cyclic quadrilateral PABQ,
Thus the value of
By using angle sum property in
Given PA=AB
Therefore,
Angles at the circumference subtended by the same chord are equal.
Now,
From eq. (1), (2), and (3)
Arc AQ subtends the angle
By using angle sum property in
From eq.(2) and (4)
But these are alternate angles.
Therefore, AO||BQ
24. The given figure shows a circle with centre O such that chord RS is parallel to chord QT. angle
(i). Angle QTR
(ii). Angle QRP
(iii). Angle QRS
(iv). Angle STR
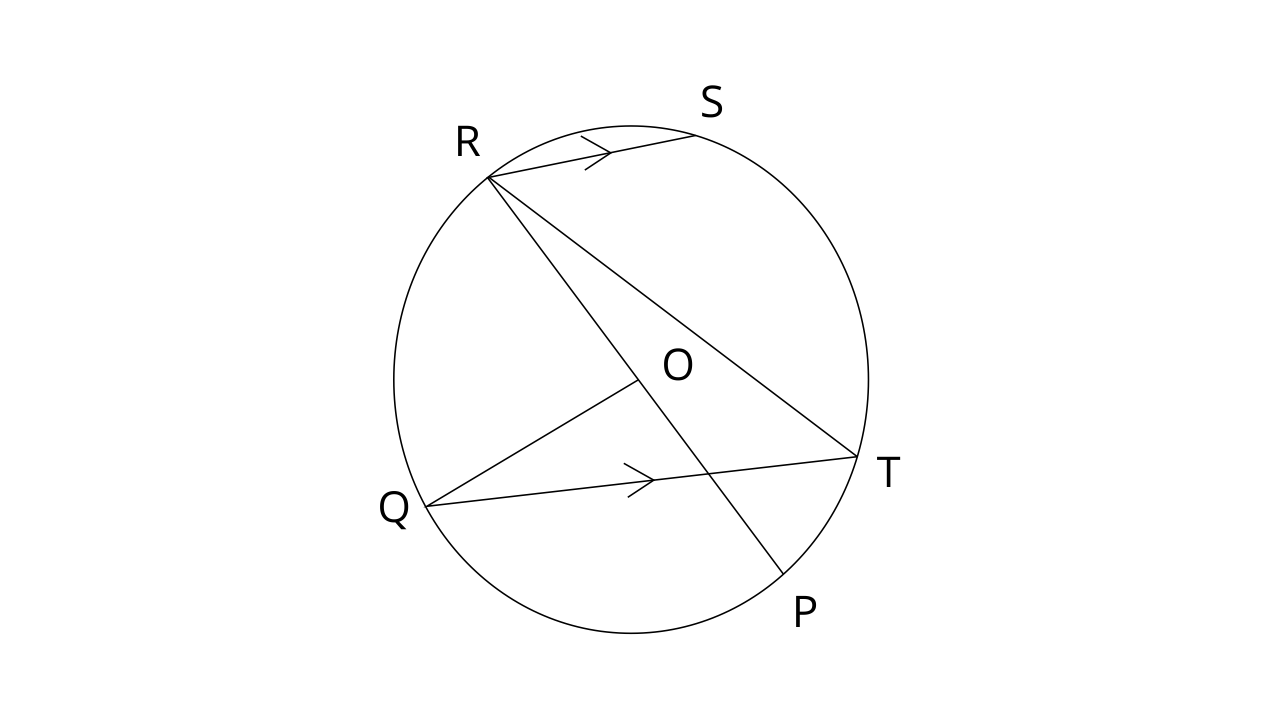
Ans: Join PQ, QR and ST
(i). Angle QTR
Ans: PR is a straight line.
In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
(ii). Angle QRP
Ans: In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
(iii). Angle QRS
Ans: Given, RS||QT
Therefore,
Now,
(iv). Angle STR
Ans: QRST is a cyclic quadrilateral.
25. In the given figure, PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that :
(i).
(ii).
(iii).
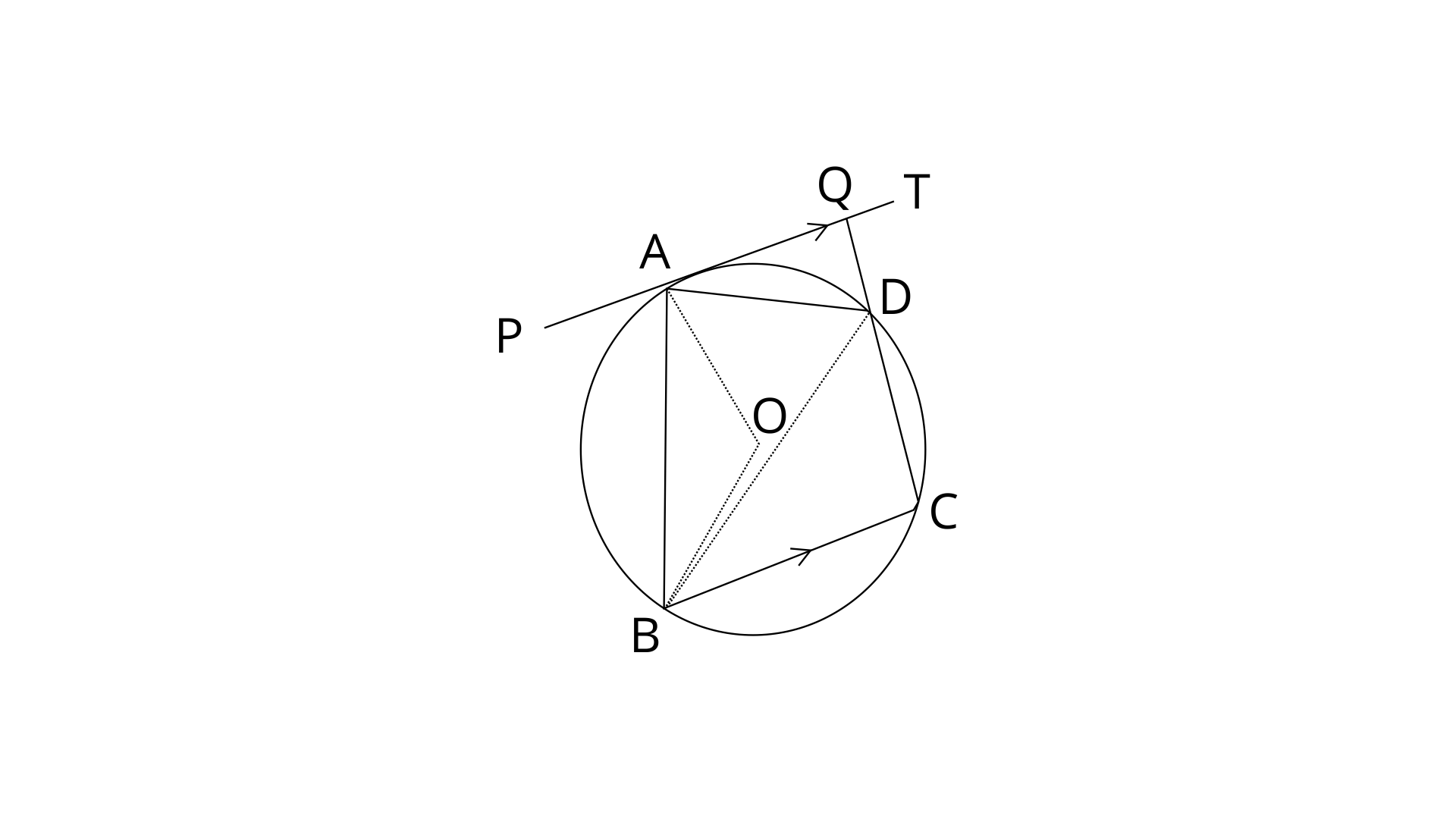
(i).
Ans: PAT||BC
Therefore,
ABCD is a cyclic quadrilateral. By using exterior angle property.
Ext.
From eq. (1) and (2)
(ii).
Ans: In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
PAT is tangent and AB is chord.
Hence,
From (i) part,
Therefore,
(iii).
Ans: ∵
Therefore,
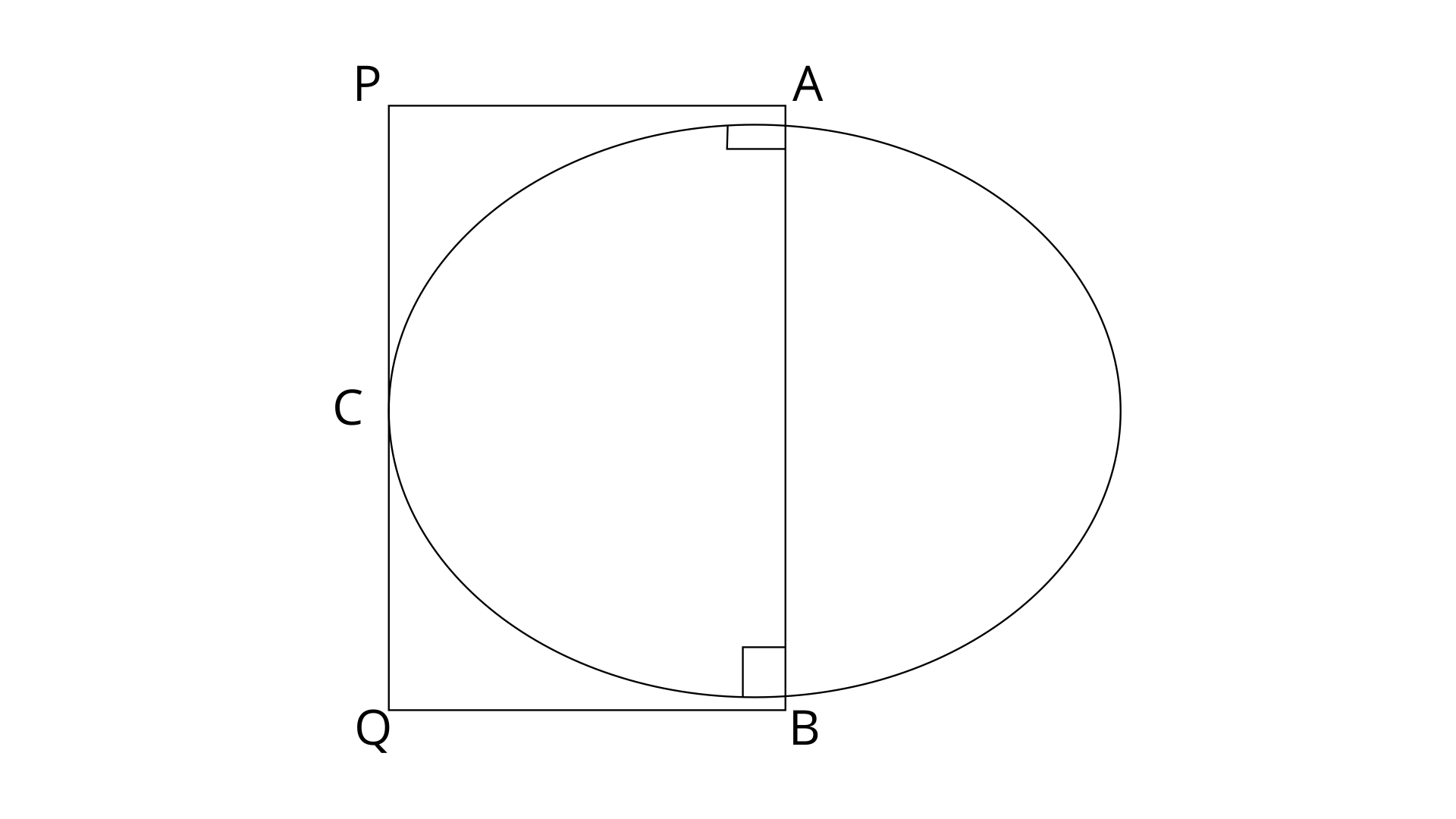
26. AB is a line segment and M is its mid-point. Three semi-circle are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all the three semi-circles. Show that :
Ans: Join OP and OQ.
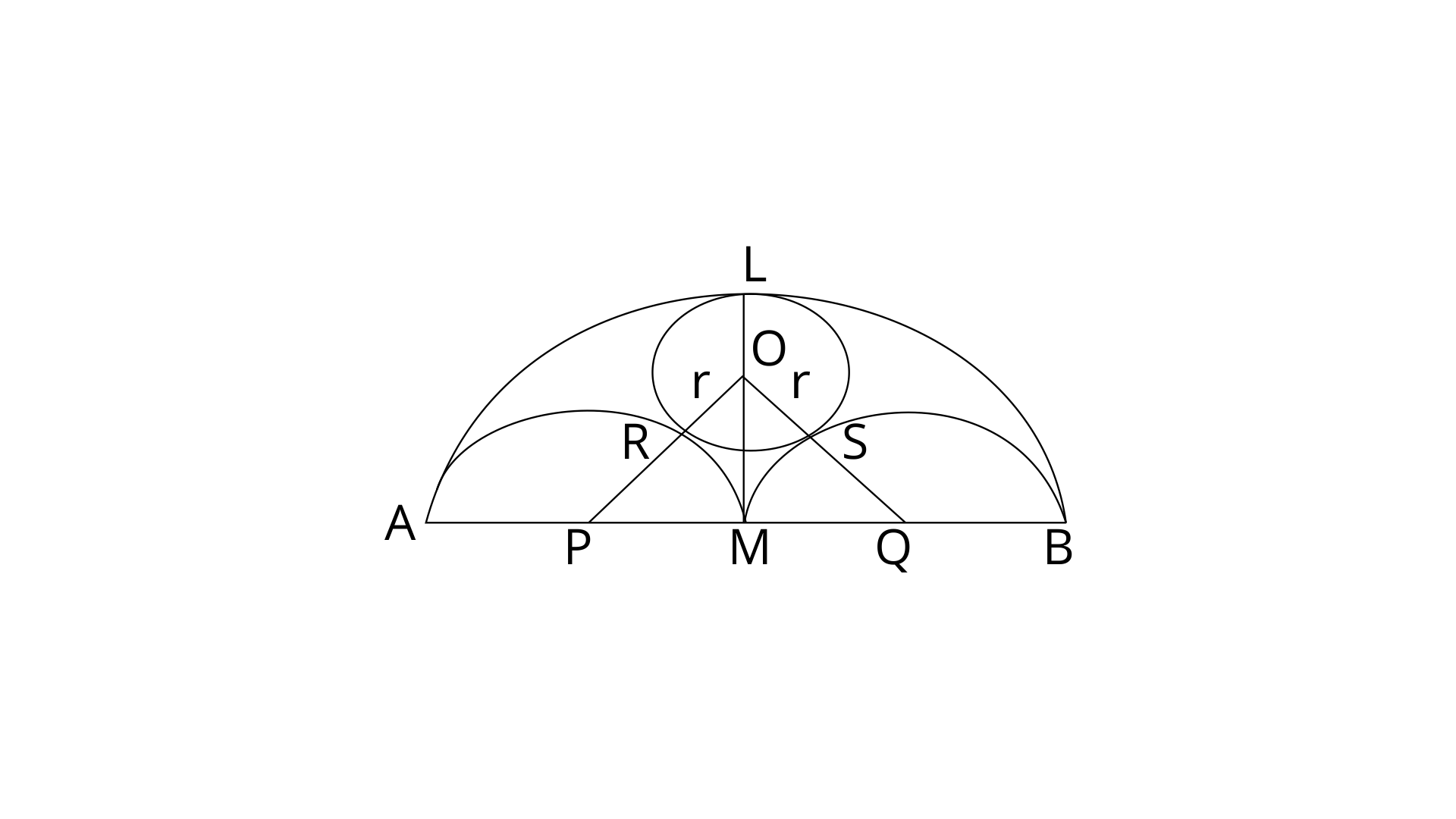
OR=OS=r
And,
Now,
Similarly,
Now,
In
$\Rightarrow
{{r}^{2}}+\frac{A{{B}^{2}}}{16}+\frac{rAB}{2}=\frac{A{{B}^{2}}}{16}+\frac{A{{B}^{2}}}{4}+{{r}^{2}}-rAB$
Hence,
27. TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Ans: Join PB.
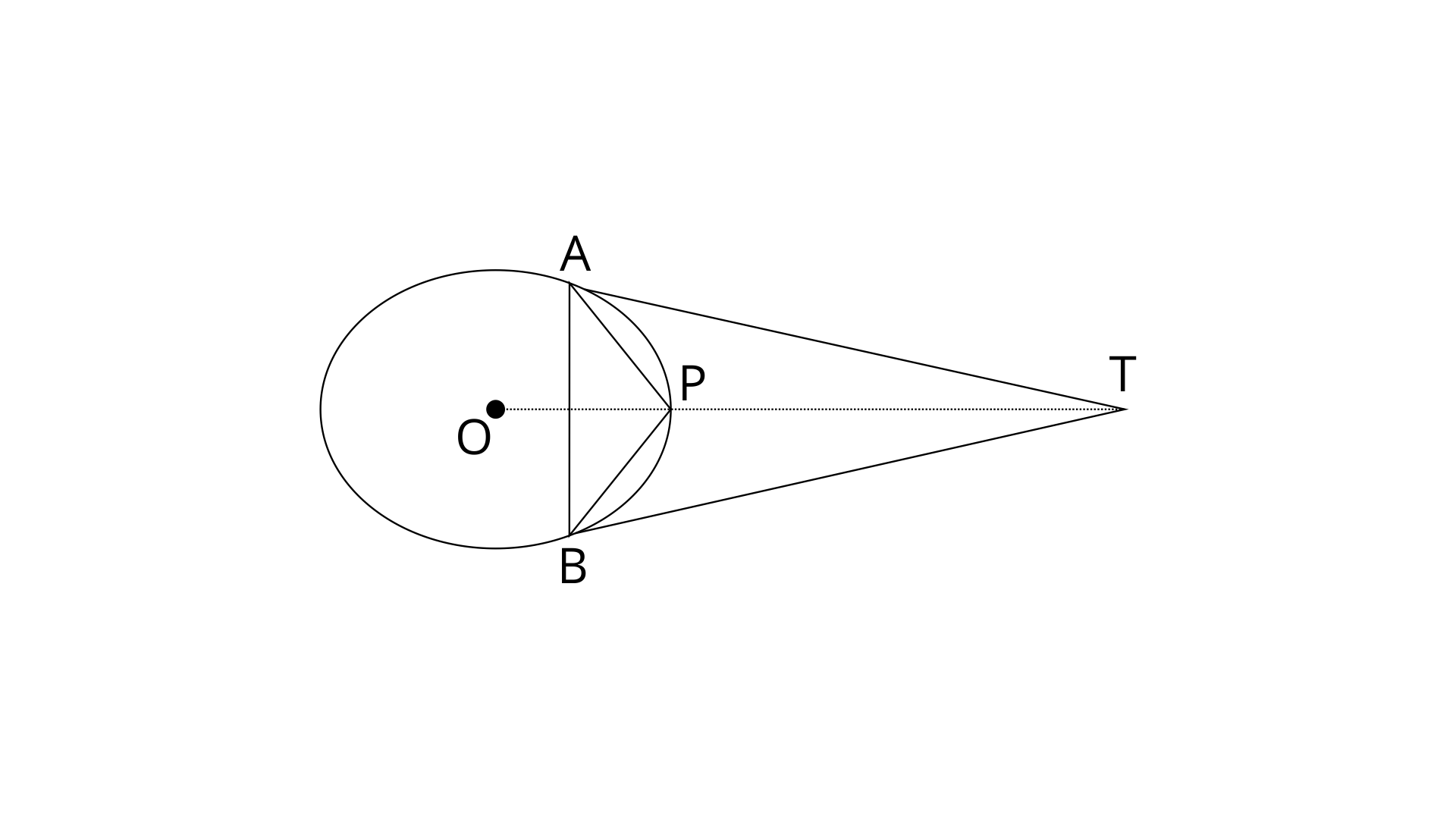
In
TA=TB (Given)
PT=PT (common sides)
Therefore,
And,
From eq. (1) and (2)
Thus AP bisects the angle TAB.
28. Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
Ans: Join PQ.
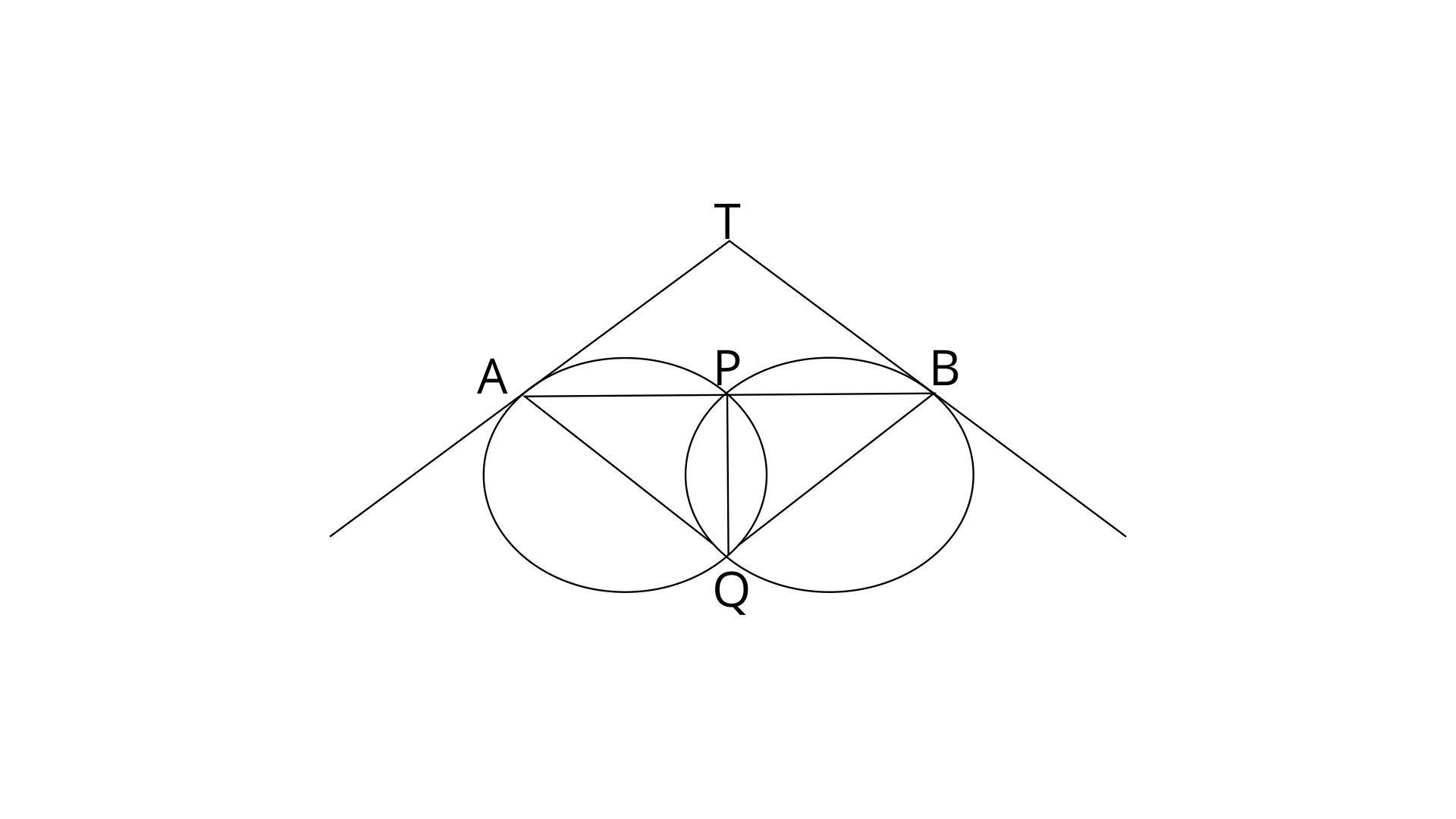
TA is a tangent and AP is a chord.
Similarly,
On adding eq.(1) and (2)
Now by using angle sum property in
The sum of opposite angles is
Thus A, Q, B and T lie on a circle.
29. Prove that any four vertices of a regular pentagon are concyclic (lie on the same circle).
Ans:
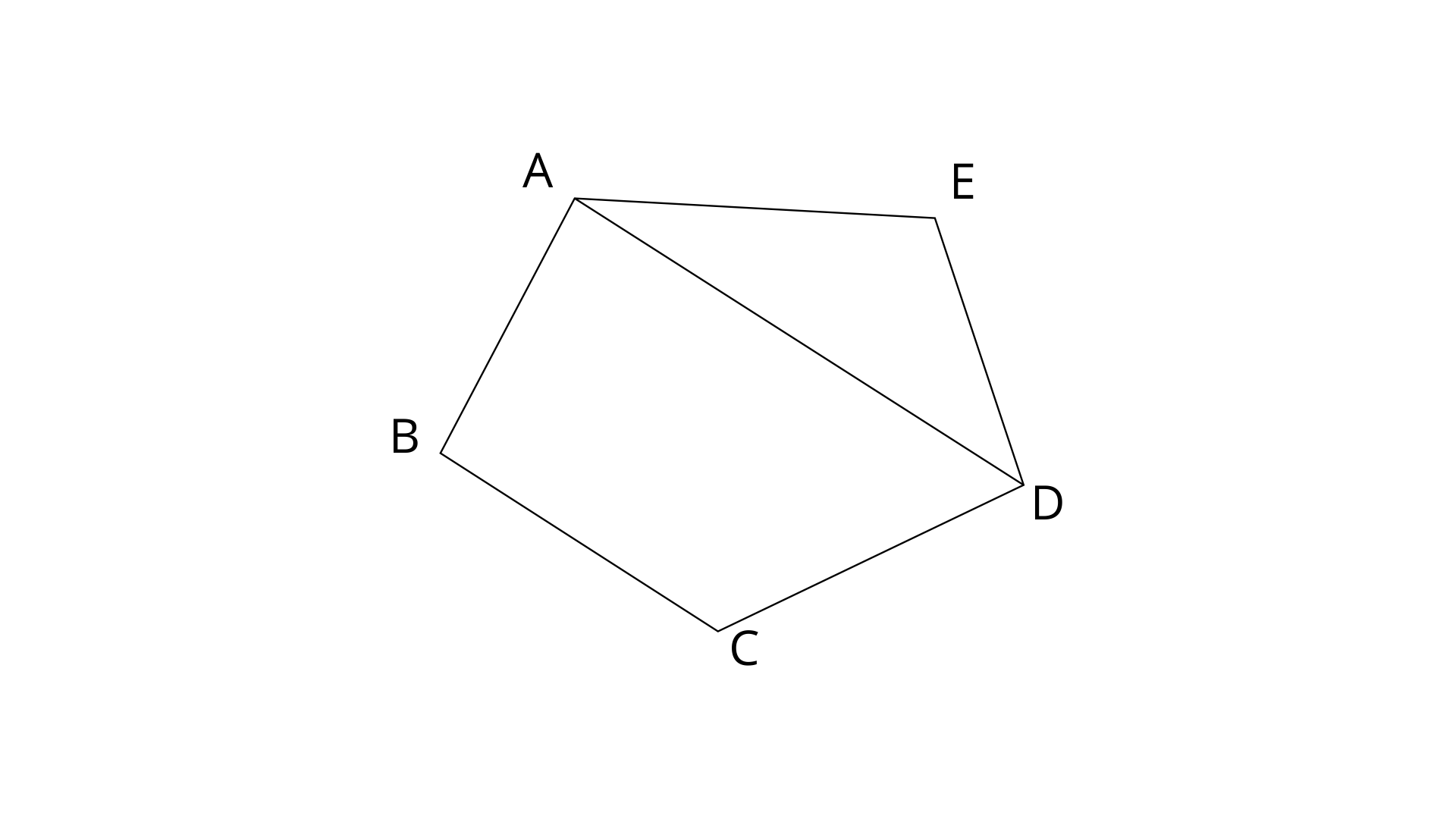
ABCDE is a regular pentagon.
Therefore,
In
AE=ED (Sides of a regular pentagon)
By using angle sum property in
Since,
Now,
In quadrilateral ABCD,
The sum of opposite angles is
30. Chords AB and CD of a circle when extended meet at point X. Given AB=4cm, BX=6cm and XD=5cm, calculate the length of the CD.
Ans:
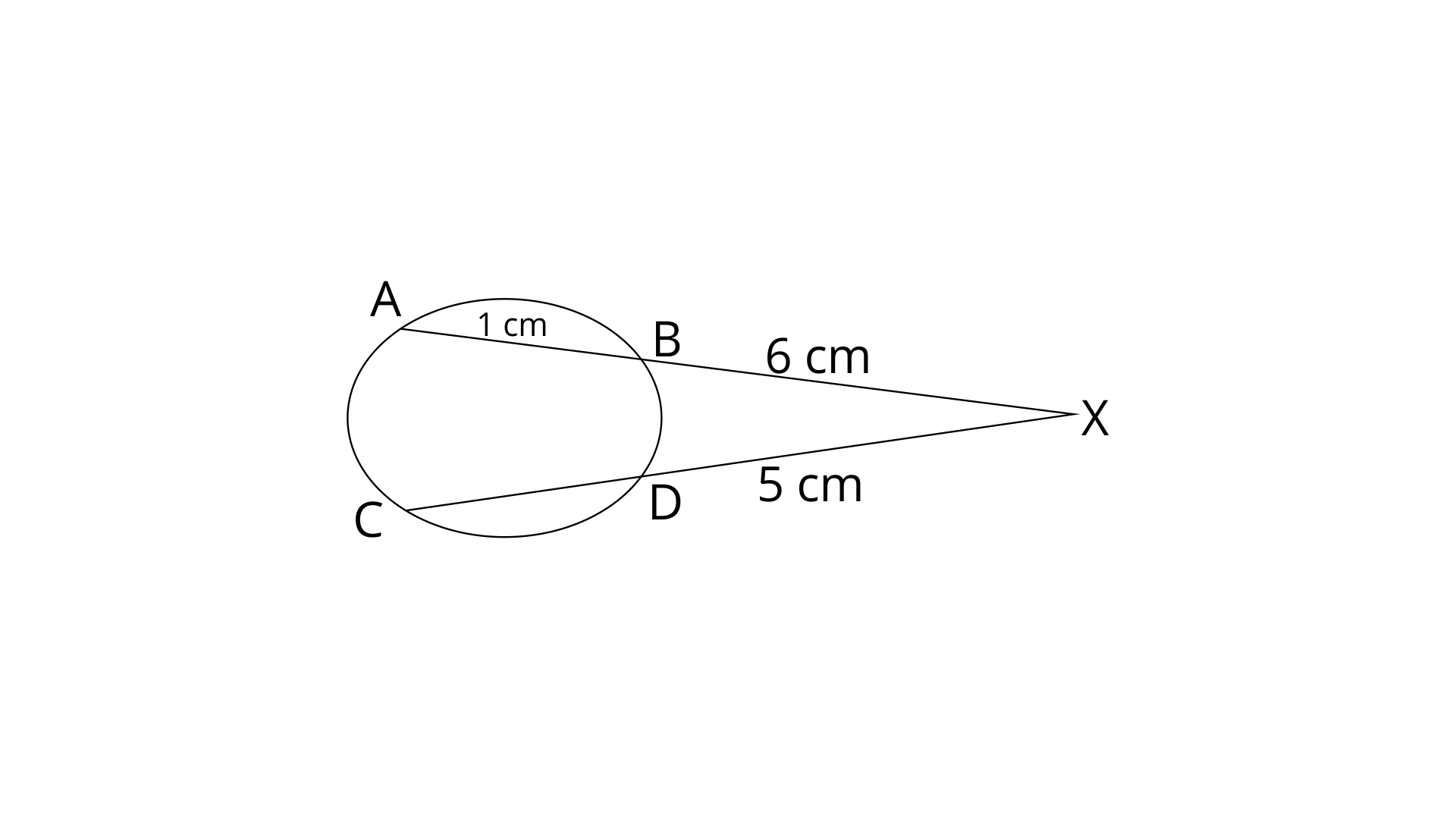
We know that,
Therefore the length of the CD is 7cm.
31. In the given figure, find TP if AT=16cm and AB=12cm.

Ans: TP is tangent and ABT is secant.
Therefore, TP=8cm.
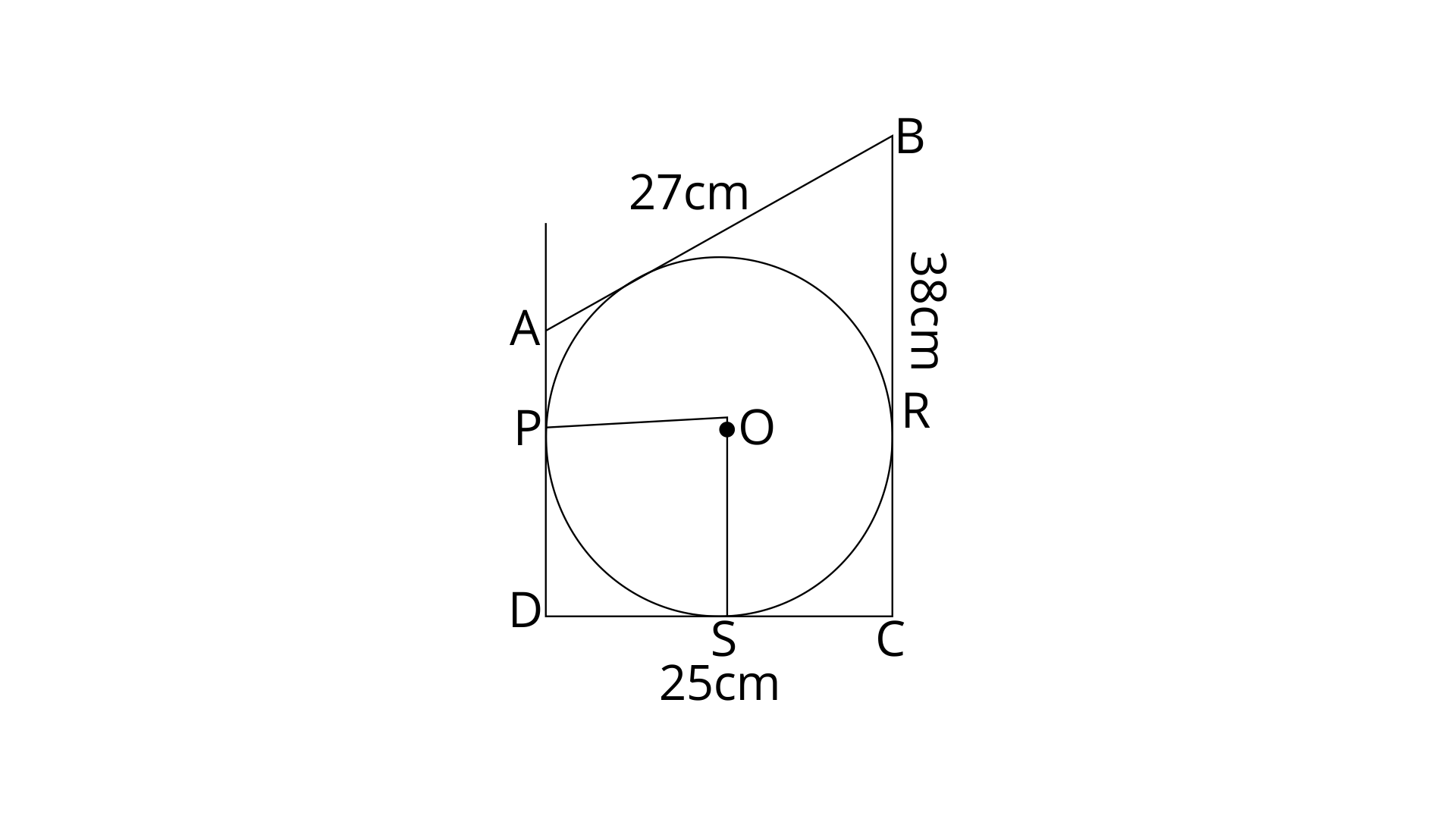
32. In the following figure, a circle is inscribed in the quadrilateral ABCD.
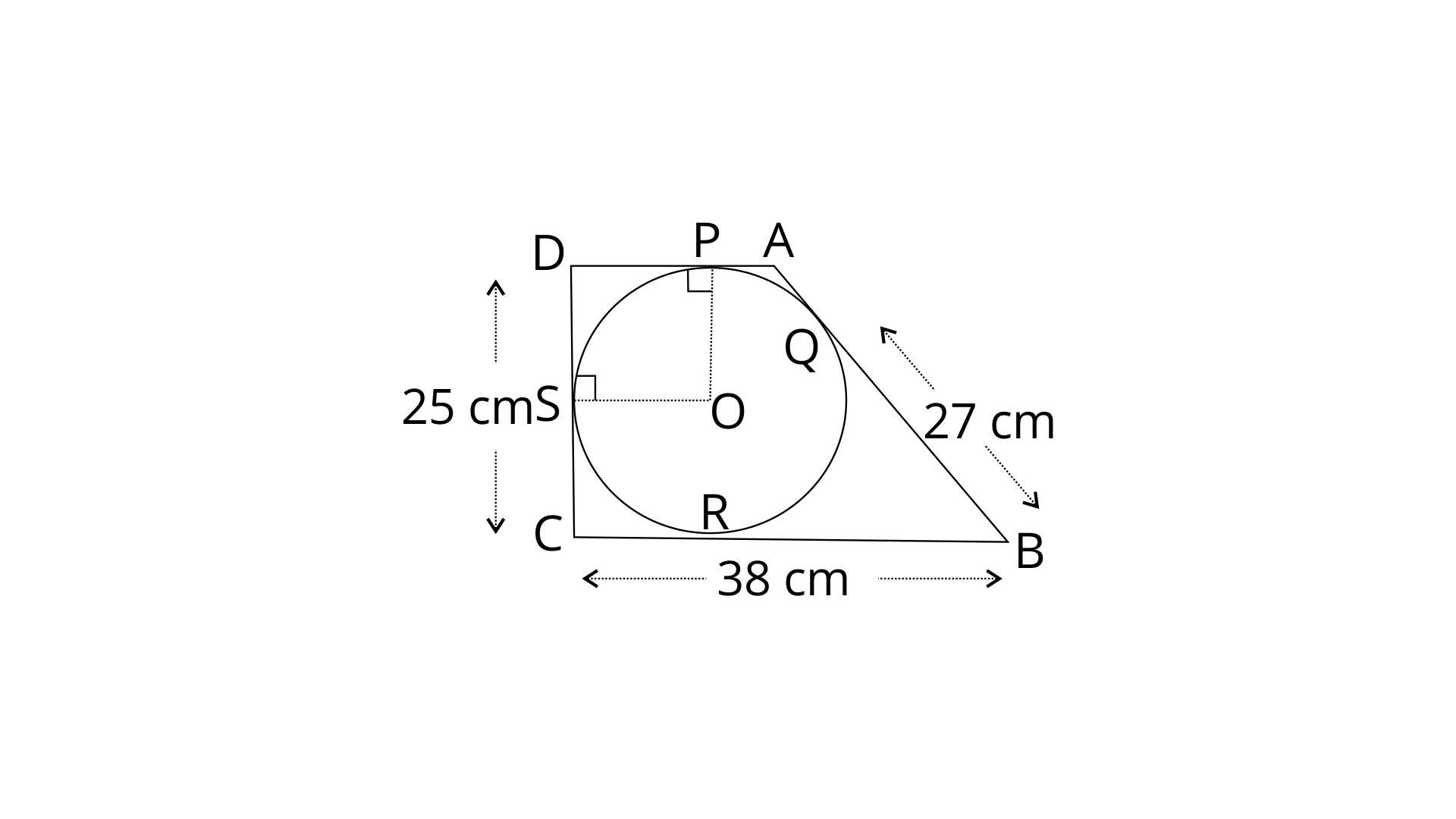
If BC=38cm, QB=27cm, DC=25cm and that AD is perpendicular to DC, find the radius of the circle.
Ans: From figure, BQ=BR (tangents to the circle from external point)
Since,
∴ CR=BC-BR=38-27=11cm
Again, CR=CS=11cm (tangents to the circle from external point)
Since, DC=25cm
∴ DS=DC-CS=25-11=14cm
Similarly, DP=DS=14cm (tangents to the circle from external point)
Now, In quadrilateral DSOP,
Therefore, DSOP is a parallelogram
Thus OP||DS and DP||OS
Now, OP=OS (Radii of same circle)
Therefore, OPDS is a square.
So, DS=OP=14cm.
Hence the radius of the circle is 14cm.
33. In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle Y.
If
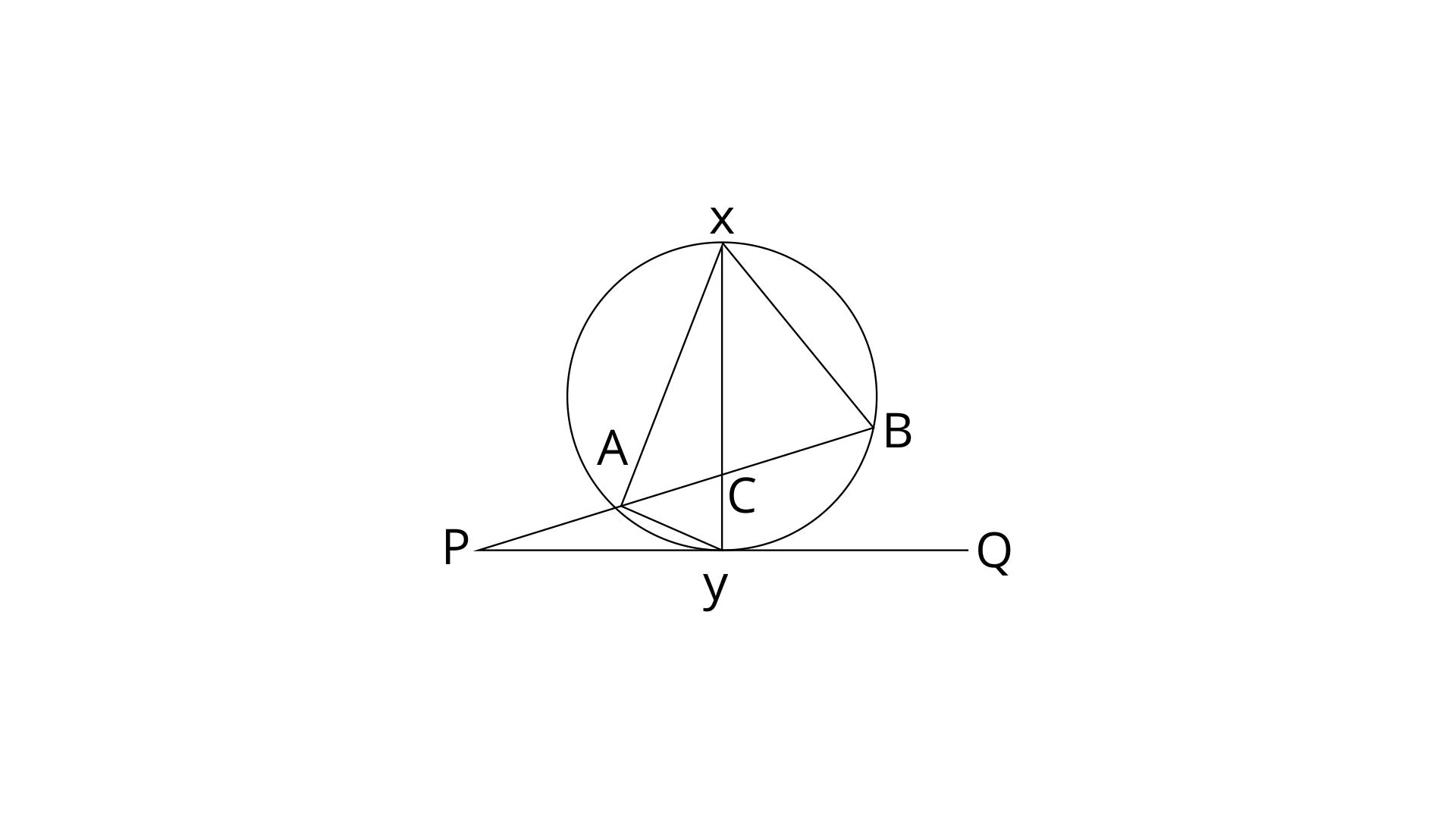
Ans: By using angle sum property in
Angle at the circumference subtended by the diameter is the right angle.
Therefore,
Since,
Angles subtended by the same chord on circumference are equal.
Therefore,
By using external angle property,
And,
By using exterior angle property,
Therefore,
34. In the given figure, QAP is the tangent at point A and PBD is a straight line.
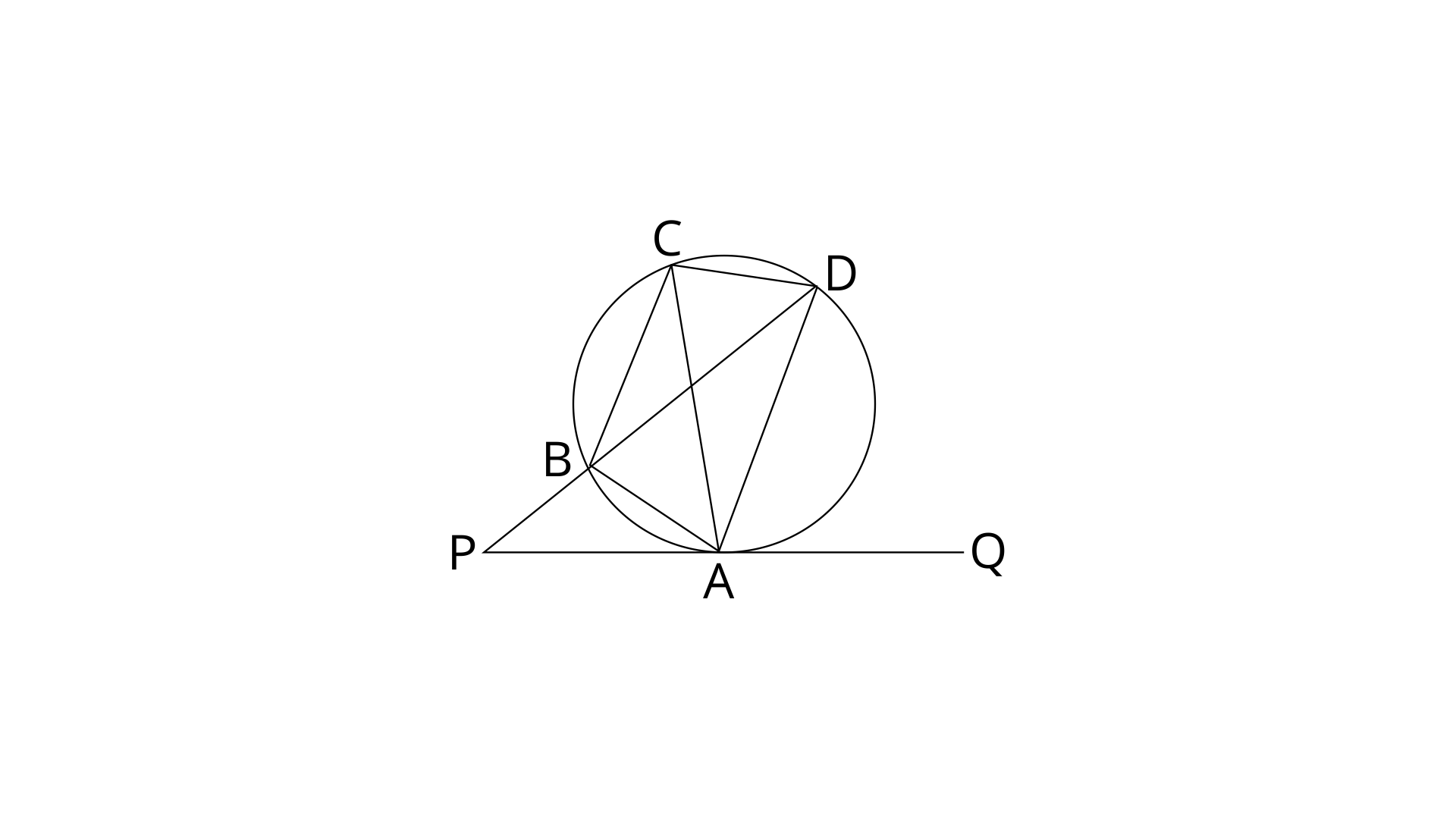
If
(i).
Ans: PAQ is a tangent and AB is a chord of the circle.
Therefore,
Thus the value of
(ii).
Ans: By using exterior angle property in
ext.
Thus the value of
(iii).
Ans: PAQ is a straight line and AD is the chord of the circle.
Thus the value of
(iv).
Ans:
Now,
Thus the value of
35. In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.
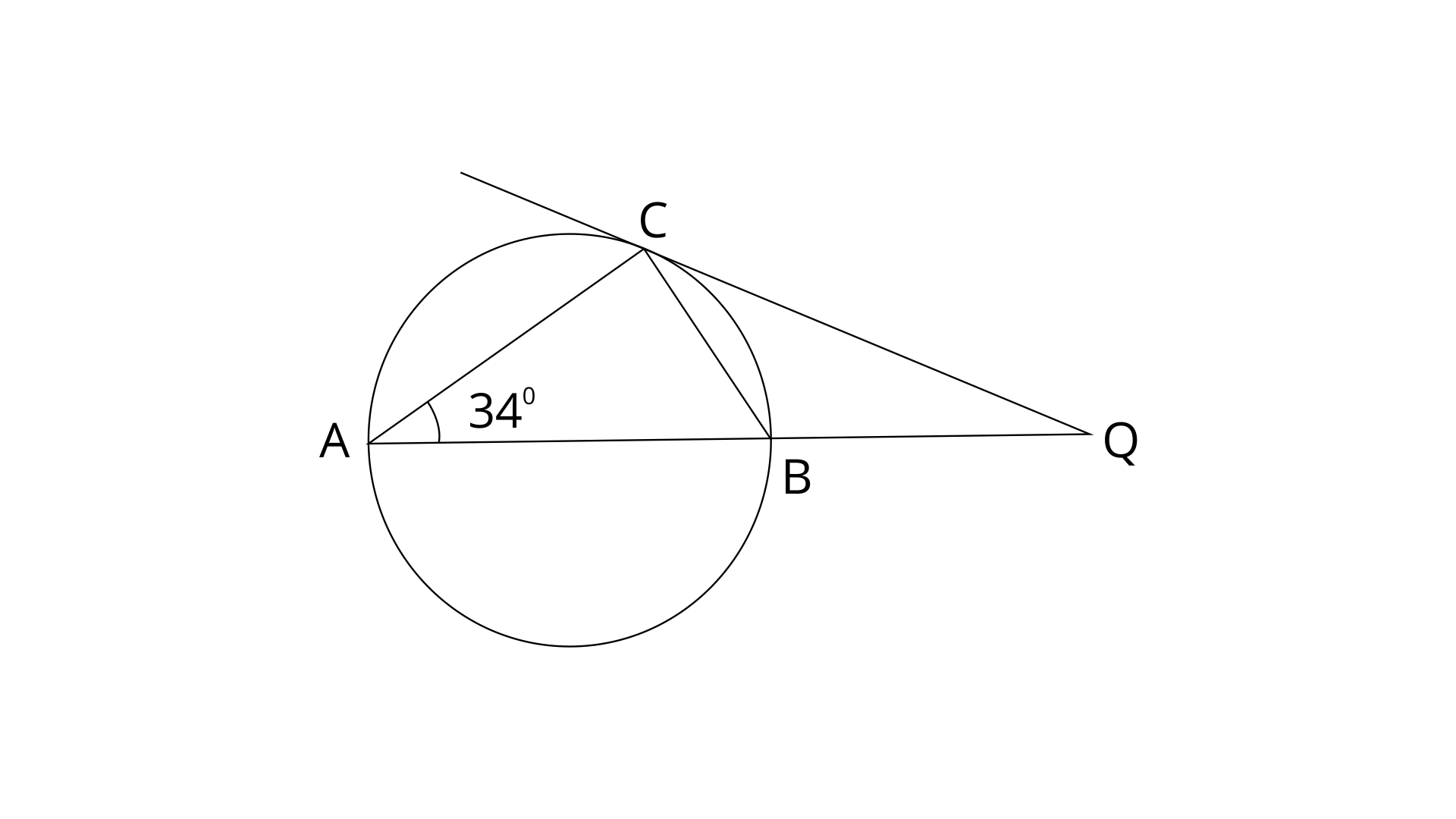
If
(i).
Ans: In a circle, Angle at the circumference subtended by the diameter is right angle. Here angle
Now by using angle sum property in
(ii).
Ans: QC is a tangent and BC is a chord.
Therefore,
ABC is a straight line, Hence
By using angle sum property in
36. In the given figure, O is the centre of the circle. The tangents at B and D intersect at B and D intersect each other at point P.
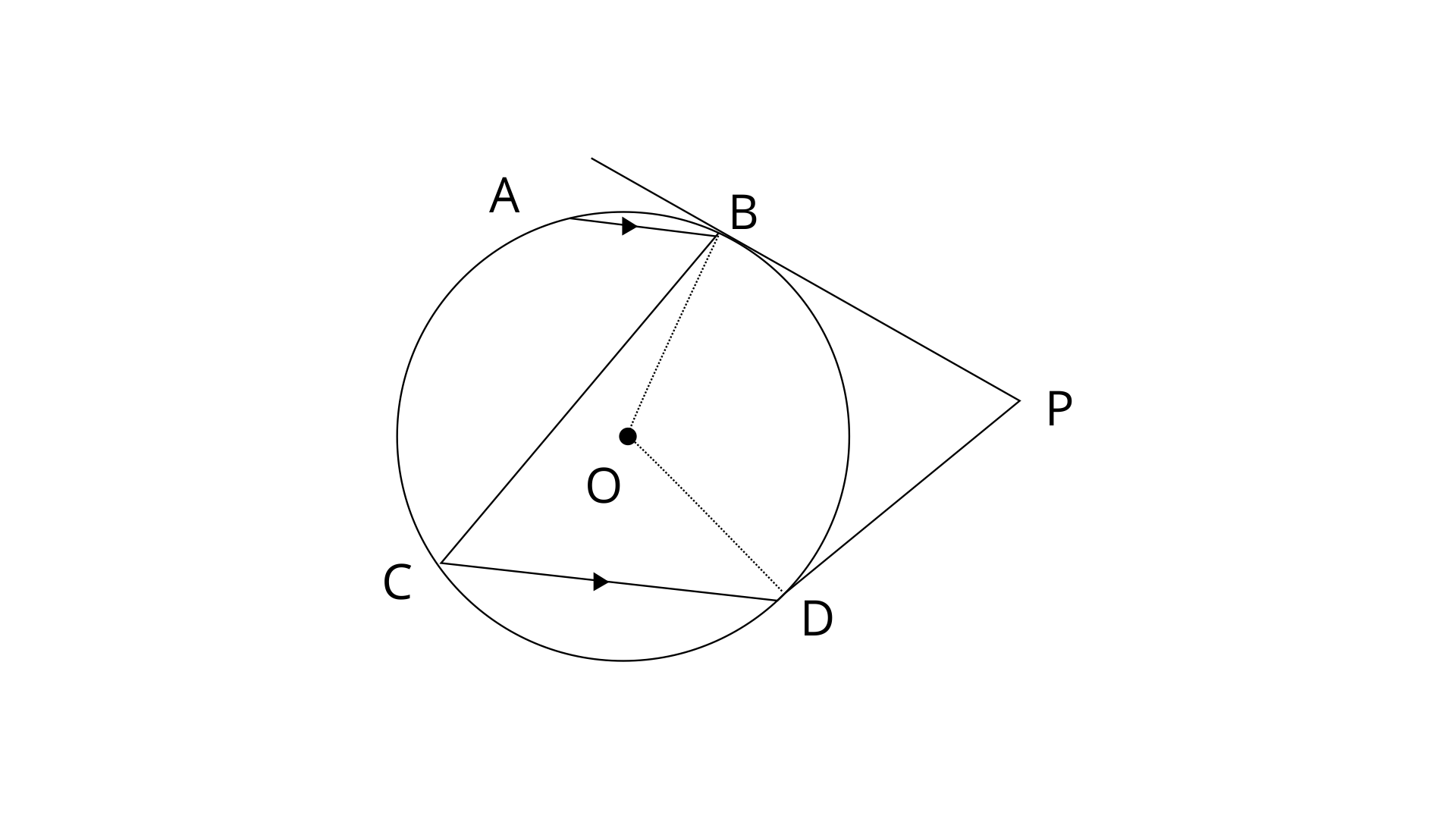
If AB is parallel to CD and
(i).
Ans: Since, AB||CD
In a circle, Angle at the centre is twice the angle at the circumference subtended by the same chord.
Therefore,
(ii).
Ans: Here PB and PD are the tangents drawn from point P and OB and OD are radius which are perpendicular to the tangents. Hence,
BPDO is a quadrilateral,
Therefore,
37. In the following figure, PQ=QR,
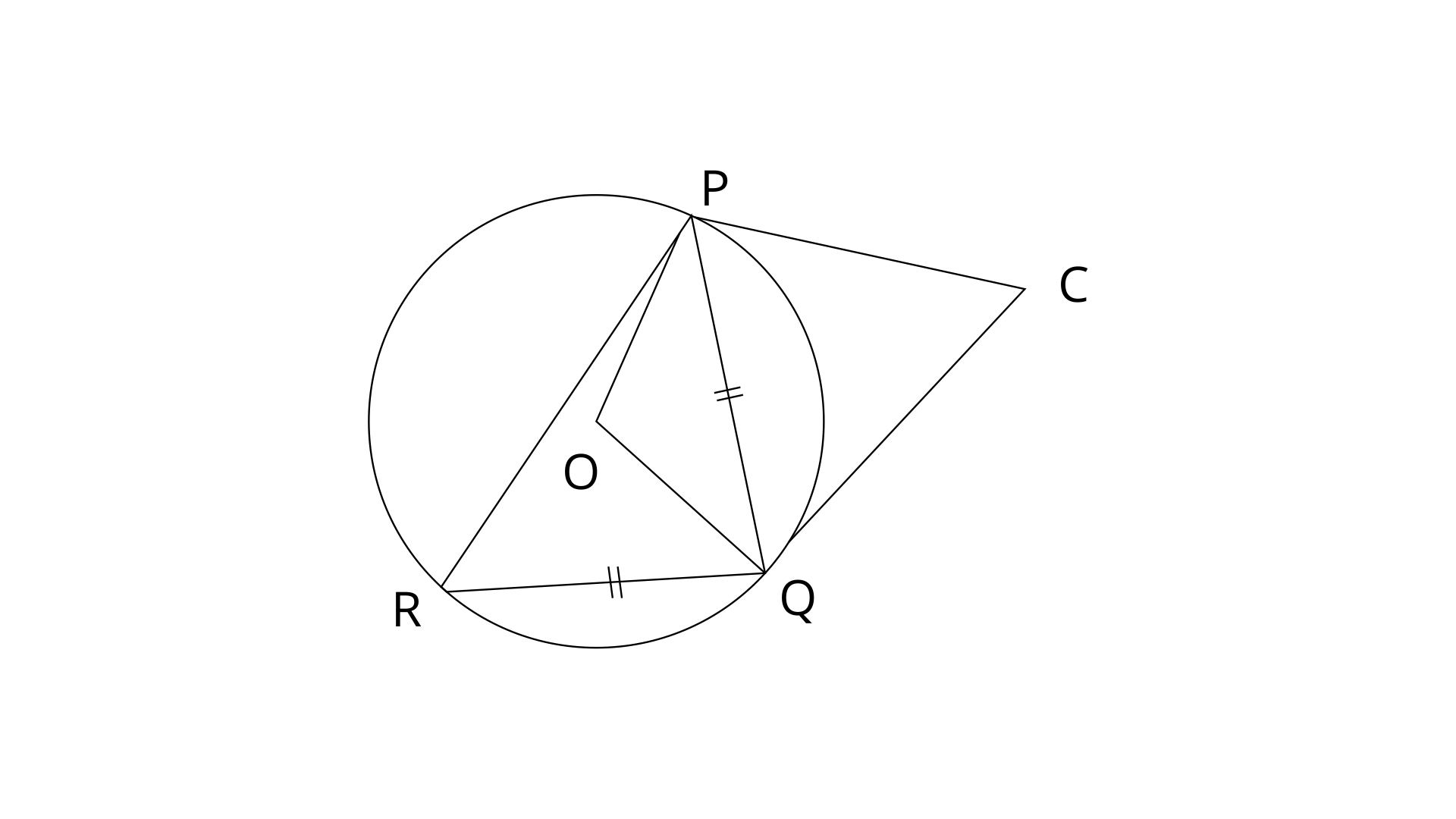
Calculate the values of :
(i).
Ans: Since, PQ=PR
By using angle sum property in
In a circle, Angle at centre is doubled the angle at the circumference subtended by the same chord.
Now,
(ii).
Ans: PC is a tangent and PQ is a chord.
Therefore,
Similarly,
By using angle sum property in
38. In two circles, prove that all the chords of the outer circle, which touch the inner circle, are of equal length.
Ans:
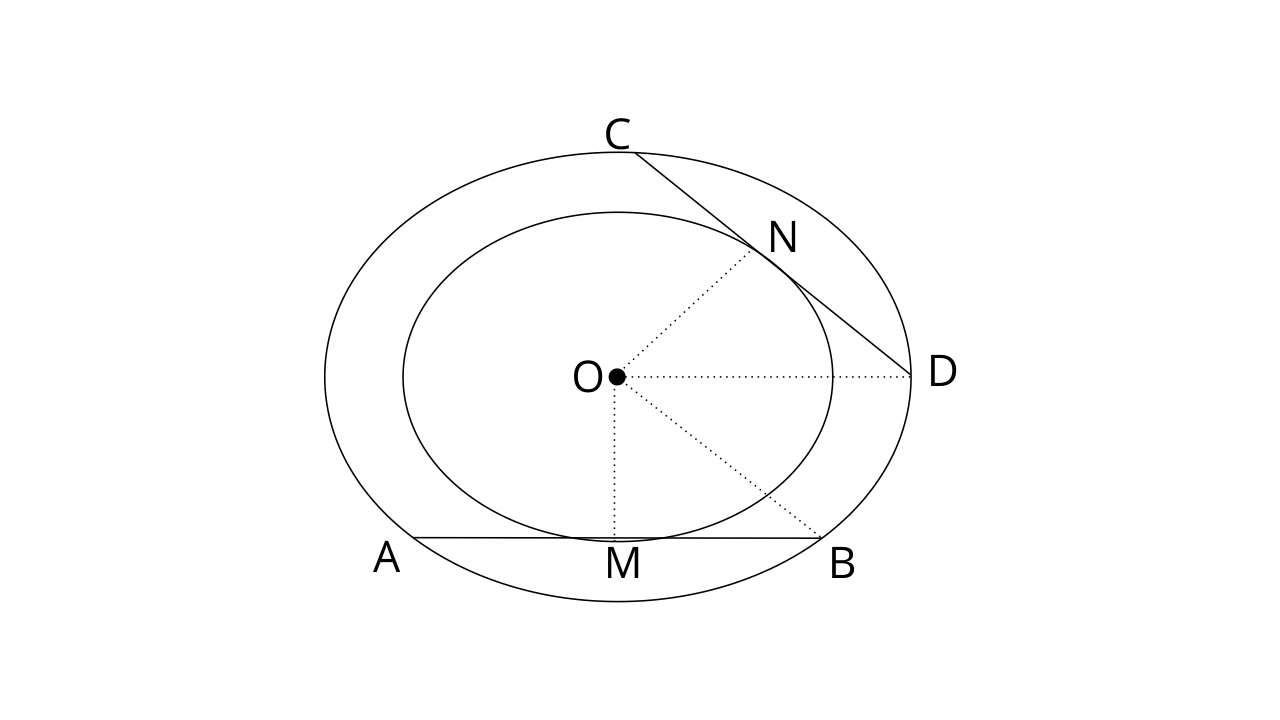
Consider the following two concentric circles with centres o.
Let AB and CD are two chords of the outer circle and touch the inner circle at point M and N respectively.
We have to prove the chords are equal, that means AB=CD.
We join points OM, OB, ON, OD.
Here OM and ON are the radius of the inner circle. Let the radius is r.
So, OM=ON=r
Similarly , Let R is the radius of the outer circle. OB=OD=R
AB is tangent to the inner circle and OM is radius and we know that the radius is perpendicular to the tangent.
Similarly,
By using pythagoras theorem in
And,
From eq. (1) and (2)
AB=CD (Hence proved)
39. In the figure, given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6cm and 3cm respectively.
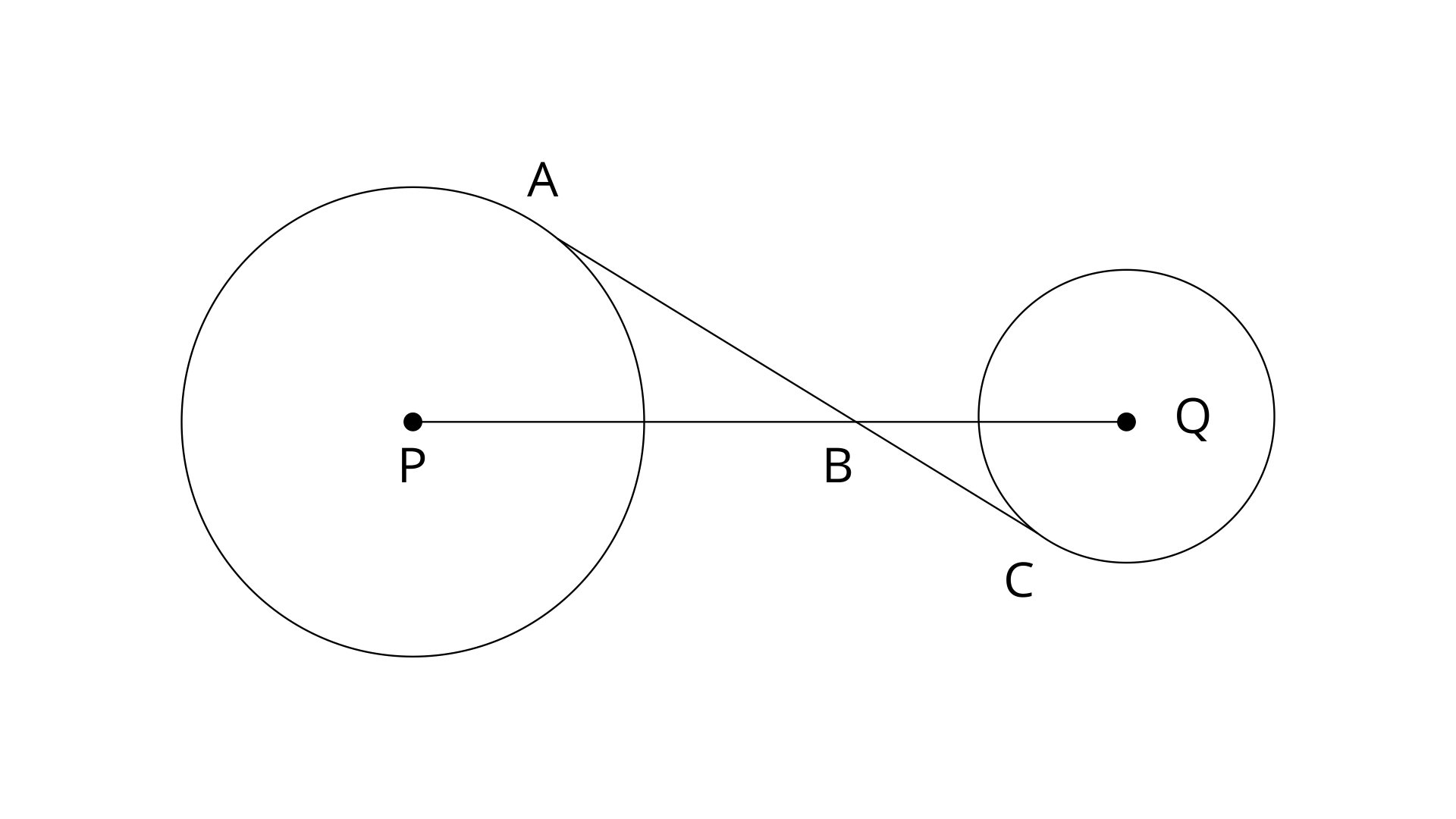
Given that AB=8cm, calculate PQ.
Ans:
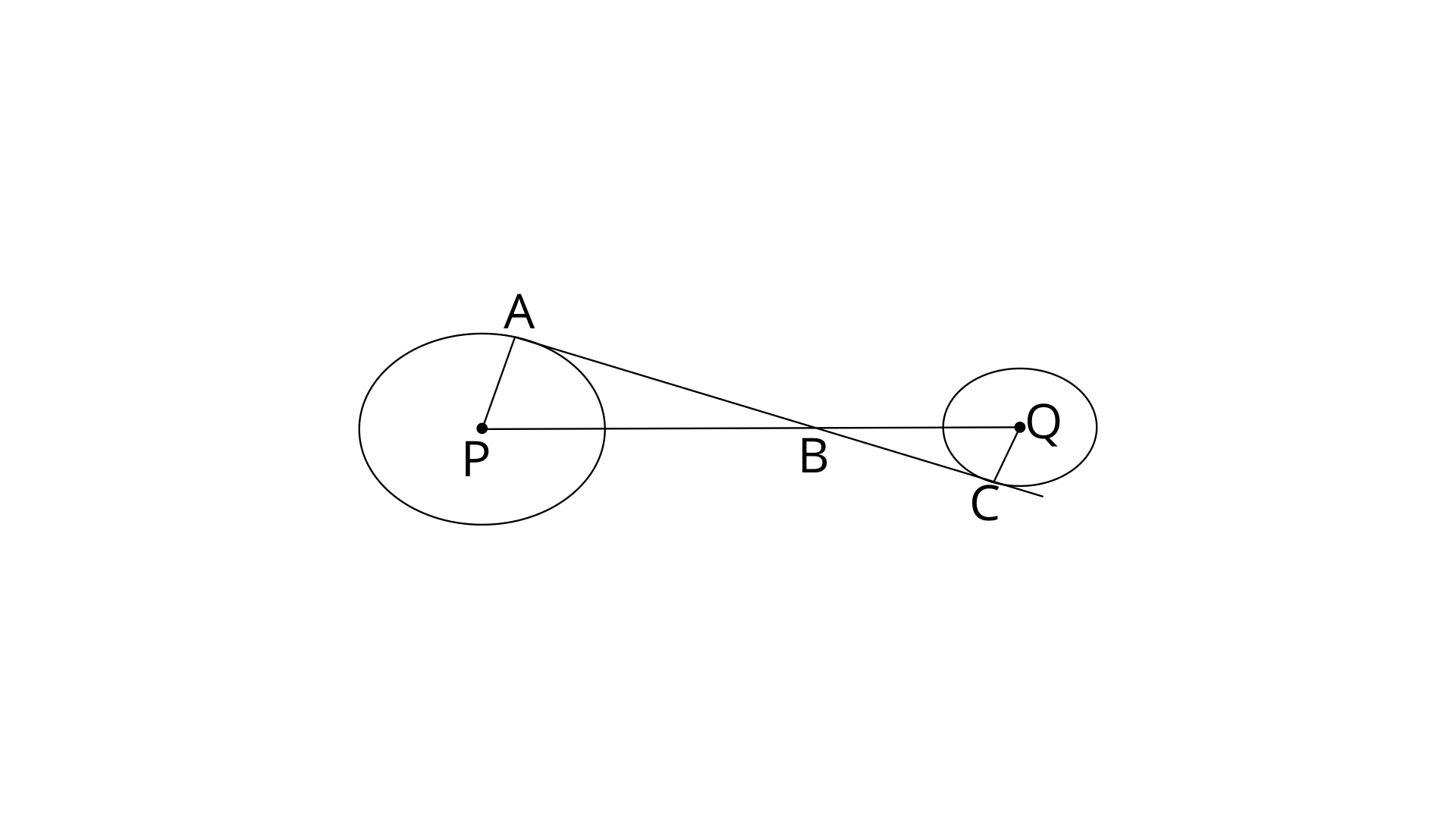
Since AC is tangent to the circle with centre P at point A.
Therefore,
Similarly,
In
Therefore,
By using pythagoras theorem in
From (i) and (ii)
Now,
40. In the figure, given below, O is the centre of the circumcircle of triangle XYZ.
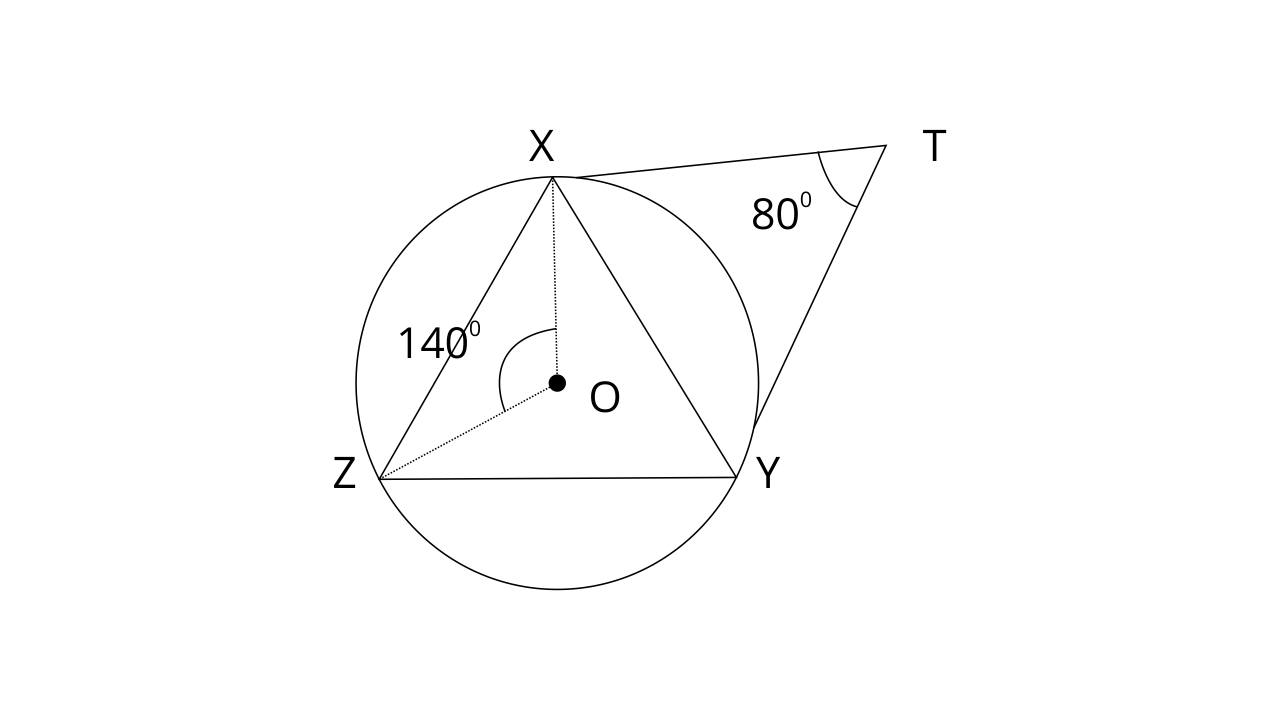
Tangents at X and Y intersect at point T. Given
Ans: Join the points OY.
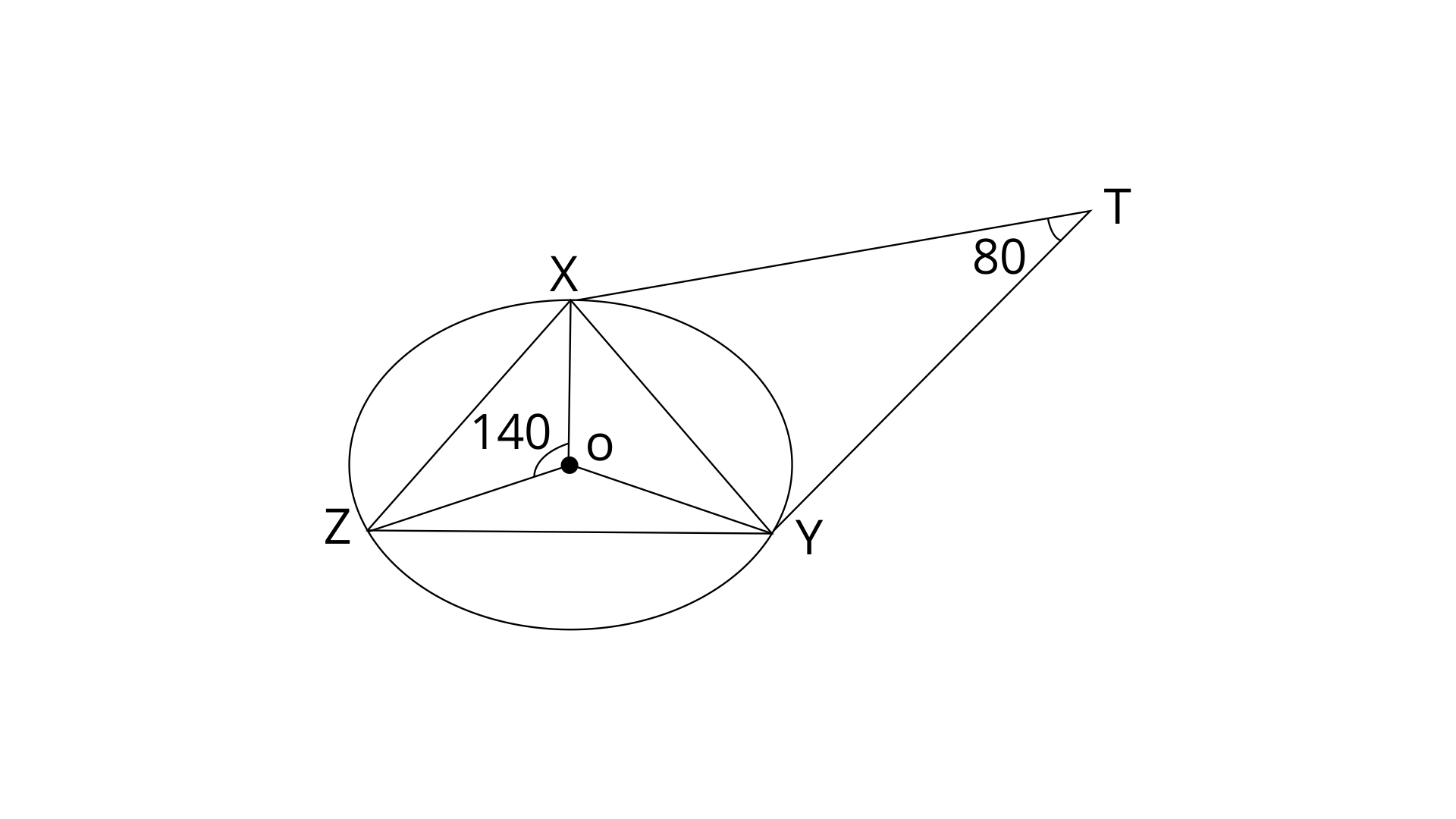
In the above figure, the circle is the circumcircle of triangle XYZ.
Given,
Tangents X and Y are intersecting at point T such that
Now,
In a circle, Angle at the centre is doubled the angle at the circumference subtended by the same chord.
Therefore,
41. In the given figure, AE and BC intersect each other at point D.
If
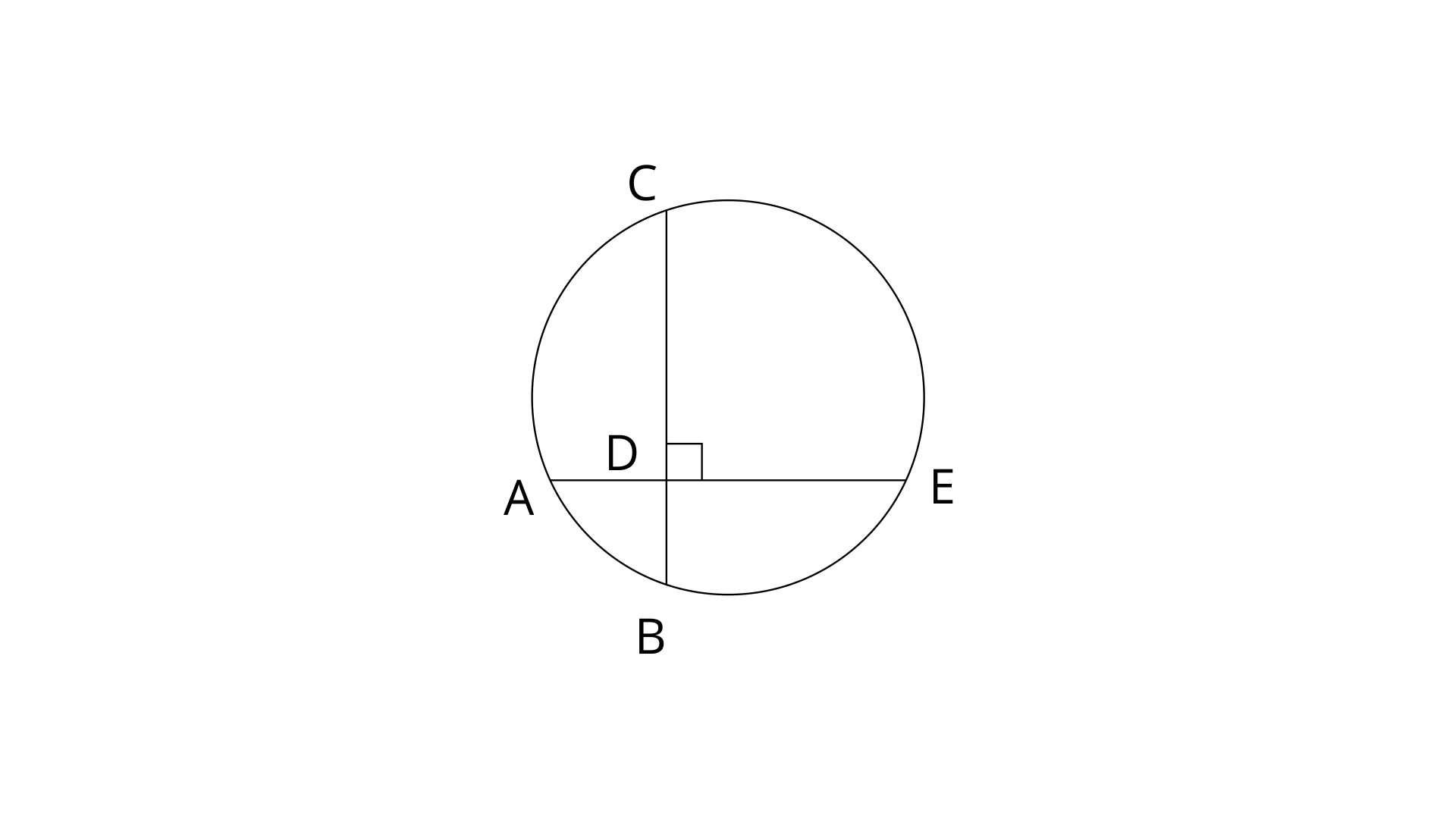
Ans: Since ADB is a right angle triangle,
By using pythagoras theorem.
Since, two chords AE and BC intersect at point D.
Hence,
42. In the given circle with centre O, angle ABC=
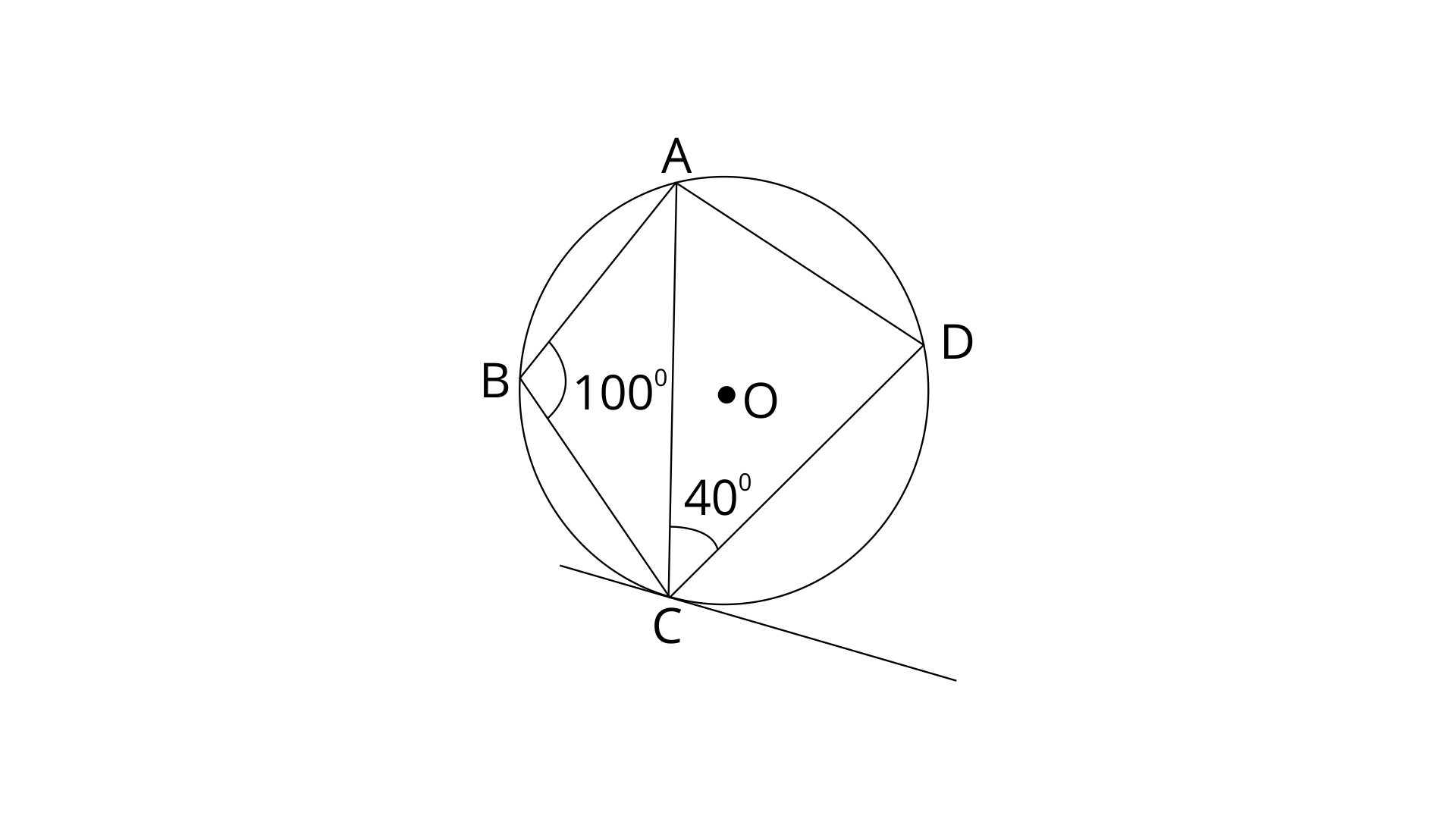
Ans: ABCD is a cyclic quadrilateral and in a cyclic quadrilateral the sum of opposite angles is
By using angle sum property in
CT is a tangent and AC is diameter,
Therefore,
Thus the value of
43. In the figure given below, O is the centre of the circle and SP is a tangent. If
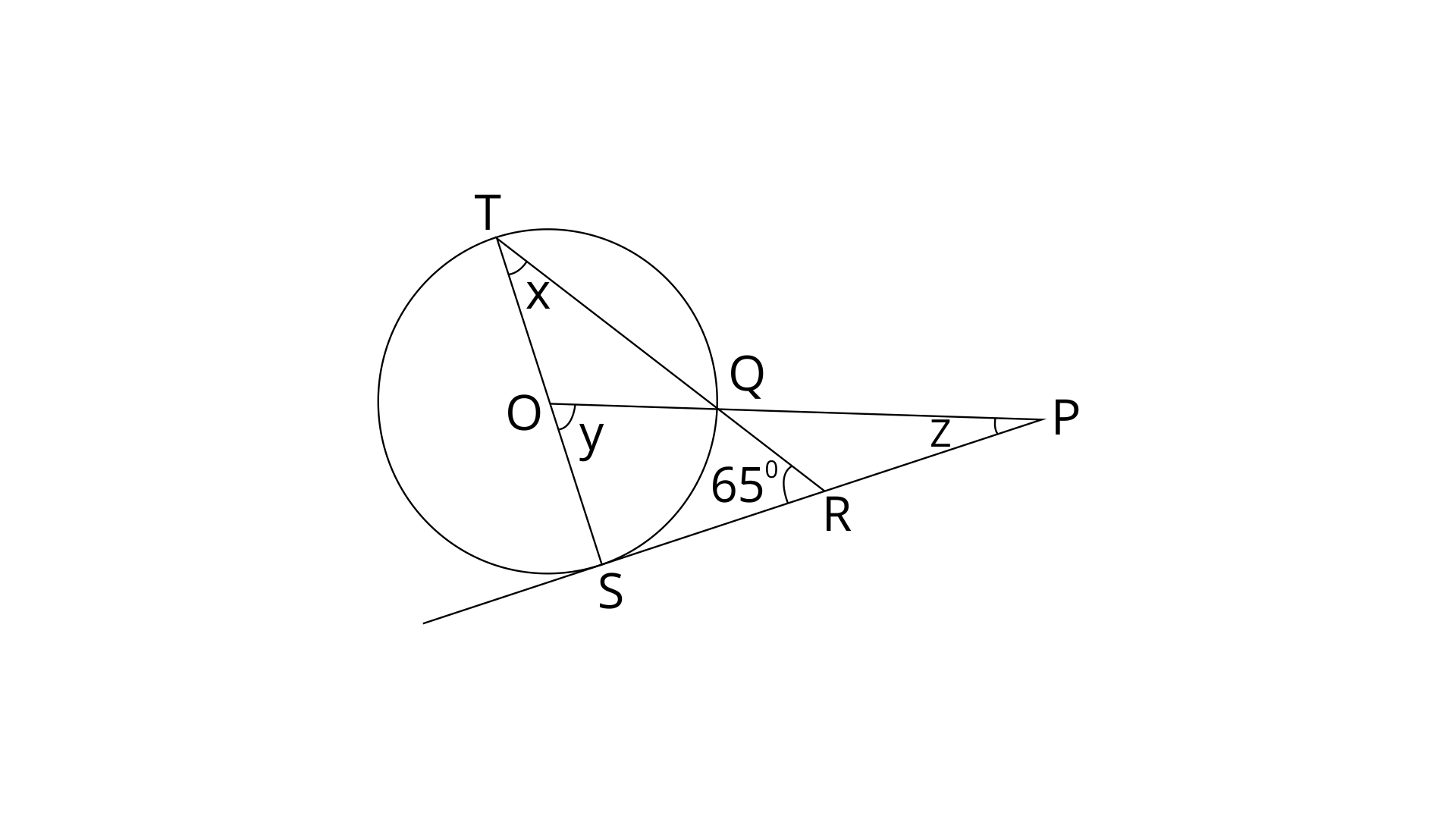
Ans: TS is diameter and PS is tangent.
Therefore,
By using angle sum property in
Angle at the centre is doubled the angle at the circumference subtended by the same Arc.
Therefore, y=2x
By using angle sum property in
Hence,
ICSE Class 10 Mathematics Chapter 18 Selina Concise Solutions
Our Vedantu Selina ICSE Solutions work as a step-by-step guide and are essential when preparing for the examination. Selina ICSE Chapter 18 Tangents and Intersecting Chords Solutions for Class 10 help you to know concepts better so that you can study anytime, anywhere.Vedantu Selina Maths ICSE Solutions Class 10 are available free of cost and include all the chapters in detail. Our Vedantu Selina ICSE Maths solutions for Class 10 act as a free guide to jump ahead in your academic life.
In order to help most students prepare for this subject and score good marks in the Class 10 ICSE board examinations, the Vedantu Selina solutions for Class 10 can be downloaded free of cost from our website. The pdf is also available for all chapters.
Vedantu Selina Solutions will help to get through the problems with proper and step wise understanding.
Let us revise the basis of tangents and intersecting chords
Introduction to the Chapter
The chapter is all about the tangents and the intersecting chords. There are many theorems related to the topics which are specified in this chapter. Students can go through the topics and in case of doubts or difficulty, they can refer to Vedantu's NCERT solution where the solutions are exactly as per the chapter and with easy explanations of the topics.
The solutions are curated to boost confidence in their ICSE preparations. The solutions also help in the problem-solving skills of the students, which are essential from an examination standpoint.
Some of the methods to be followed for the subject so that it becomes easy and you will have an organized study preparation are:
Time Table
Students should prepare an organized study schedule. Before doing this they should know the topics to be studied for each day. Once the schedule is prepared it is very important to be followed regularly. A consistent study will always be helpful to learn in a better way.
Dedicate Specific Time
Know your strengths and weaknesses. Analyze the area which needs to be given more time and dedicate the time accordingly. Maths is a challenging subject at the same time it can be easy if you practice. It is the easiest subject. The main element of getting the grip of the subject is understanding the concepts and practice.
Revise
Revision is very important and it is a continuous process so has to be done every day and not just during the exams.
Preparation of Notes
An organized note is very useful. This should contain the key points and the important topics. List of formulas and theorems that can give you a quick revision of the whole chapter.
Mock Test and the Previous Year’s Question Paper
Once the completion of the syllabus or even the chapter, you can take a mock test to see the progress of the preparation level. This will help in rectifying the mistakes as well.
Once you have completed the whole syllabus you can solve the previous year’s question paper and you will get an idea of the exact exam pattern and the types of different questions. Practicing the question's paper will give the thorough practice of the whole syllabus and the various problems.
This will also help in time management and enhance the speed while solving the problem.
Definition of Tangent
If a segment touches a circle at only one point, it is said to as Tangent to the circle.
If the point is touching the circle at more than one point, then it cannot be a tangent. The tangents of a circle have the following properties.
A tangent touches the boundary of the circle at only one point.
A tangent is perpendicular to the radius of the circle at the point of contact.
Tangents cannot be drawn through a point which lies in the interior of the circle.
Two tangents can be drawn to the circle from the point outside a circle.
Every point on the circle has one and only one tangent passing through it.
(Image will be Uploaded soon)
Length of Tangent Theorem
Only two tangents can be drawn to a circle from a point external to the circle. These two tangents will have the same length. Length of tangent to the circle from an external point can be calculated as given
l =
In the above equation,
‘l’ is the length of the tangent
d is the distance between the center of the circle and the external point from which the tangents are drawn
‘r’ is the radius of the circle
Key Features of Vedantu Solutions
Easy & reliable solutions
Available free of cost
Highlight important examination questions
Step-by-step solutions for all questions
Prepared by subject experts
Designed according to the latest ICSE syllabus pattern
Available online 24/7
In-depth knowledge of the chapter is provided in easy language.
Is based on the latest ICSE syllabus.
Best study material to prepare for the Class 10 ICSE board exam.
All the doubts that might arise while solving the exercise questions will vanish by going through these Vedantu Selina solutions
The Vedantu Selina Maths Solutions are designed to give maximum information to students preparing for the board examinations. By referring to Vedantu Solutions, students can grasp the concepts behind the solutions very quickly. This will not only aid students by giving them the confidence to answer all sorts of questions in the examinations but will also ensure that they learn the concepts in the long run as well. The Vedantu Selina Maths Chapter 18 Tangents and Intersecting Chords Solutions Class 10 focuses on answering the questions in the right way to encourage students to fetch full marks in the examination.
In ICSE Class 10, Maths is one of the challenging subjects of all as it includes all chapters. The chapters presented in the textbook are hard, and students often get confused about what is the right solution. Vedantu provides Selina Maths Chapter 18 Tangents and Intersecting Chords Solutions for ICSE Class 10 so that they can study well in their examination. All the Selina Maths Solutions are created by our experts who have vast academic experience.
Vedantu Selina Concise Maths Solutions for Class 10 is perfect for preparing for the board examinations. ICSE Class 10 syllabus is vast and needs concentrated efforts on the part of the students to face the examinations and shine out successful. The Vedantu Selina Concise Maths Class 10 ICSE solutions pdf includes details for all chapters from the subject. This will allow the students to examine and understand every concept even if practising for the first time.
Vedantu Selina ICSE Chapter 18 Tangents and Intersecting Chords Solutions for Class 10 all questions are answered and explained by expert teachers as per ICSE board guidelines. By referring these Vedantu Selina ICSE Solutions for Class 10 you can easily get high marks in ICSE Class 10 Board Examinations.
FAQs on Concise Mathematics Class 10 ICSE Solutions for Chapter 18 - Tangents and Intersecting Chords
1. What are the basic concepts of chapter 18 of class 10 ICSE?
The basic concept is that if the circle and the straight line are drawn in the plane. There will be three possibilities that the line will not meet the circle, the second possibility is that it intersects the circle at two points. The line meets the circle at only one point.
The line that touches the circle at only one point is known as the secant of the circle. These details have to be learned thoroughly so that you can solve the problems easily related to these topics. When you get the clarity of the concepts it becomes very easy.
2. Which are the best reference books for class 10 chapter 18?
According to Theorem 19, if two circles touch each other their point of contact is a straight line through the centers.
Theorem 20 states that if two chords of the circle intersect either internally or externally then it is proved that the product of the lengths of the segments is equal. These are the statements but students have to learn to prove with proper steps and giving reasons. The theorems are easy to score if they are properly presented with all the steps.
4. What does theorem 21 and 22 state in chapter 18 of class 10 ICSE Maths?
According to theorem 21, the angle between the tangent and a chord through the point of contact is equal to the angle in the alternate segment.
According to theorem 22, if the chord and the tangent intersect externally then it is said that the products of the lengths of the chord are equal to the square of the length of the tangent from the two points that are the point of contact and the point of intersection.
5. What are the advantages of referring to ICSE Solutions from Vedantu?
The advantages of preparing class 10 ICSE Maths from ICSE solutions from Vedantu are below.
The solutions are all prepared by experts who have excellent subject knowledge. The topics are very well structured and organized which is very easy to understand. Even the complex solutions or the problems are simplified which helps in comprehensive understanding. If students can solve all the problems in the ICSE solutions perfectly then there is nothing to worry about and they are sure to have success in the exam. Keep in mind to avoid silly mistakes and always read the questions properly before solving the problem.





































