ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions - Free PDF Download
You can find Selina Concise Mathematics Class 10 ICSE Solutions for Chapter 22 Height and Distance on the website of Vedantu. The PDF includes comprehensive solutions to all the questions asked in ICSE Class 10 Mathematics Chapter 22 Selina textbook. In order to excel in the board exam with good grades and to have a strong grip on Chapter 22 Heights and Distances, students are advised to download ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions as answers to each question are properly explained in a structured way. This will help you to clear the basic concept of the chapter effectively.
ICSE Class 10 Mathematics Chapter 22 Solutions are prepared by the professionals as per the latest ICSE syllabus issued by the ICSE board. By practising the questions given in the PDF repeatedly, you will be able to solve the complex questions given in each exercise more easily.
Access ICSE Selina Solutions for Grade 10 Mathematics Chapter 22 – Heights and Distances
EXERCISE 22(A)
1. The height of a tree is
Ans: Let the length of the shadow of the tree be
Therefore the height of the tree is
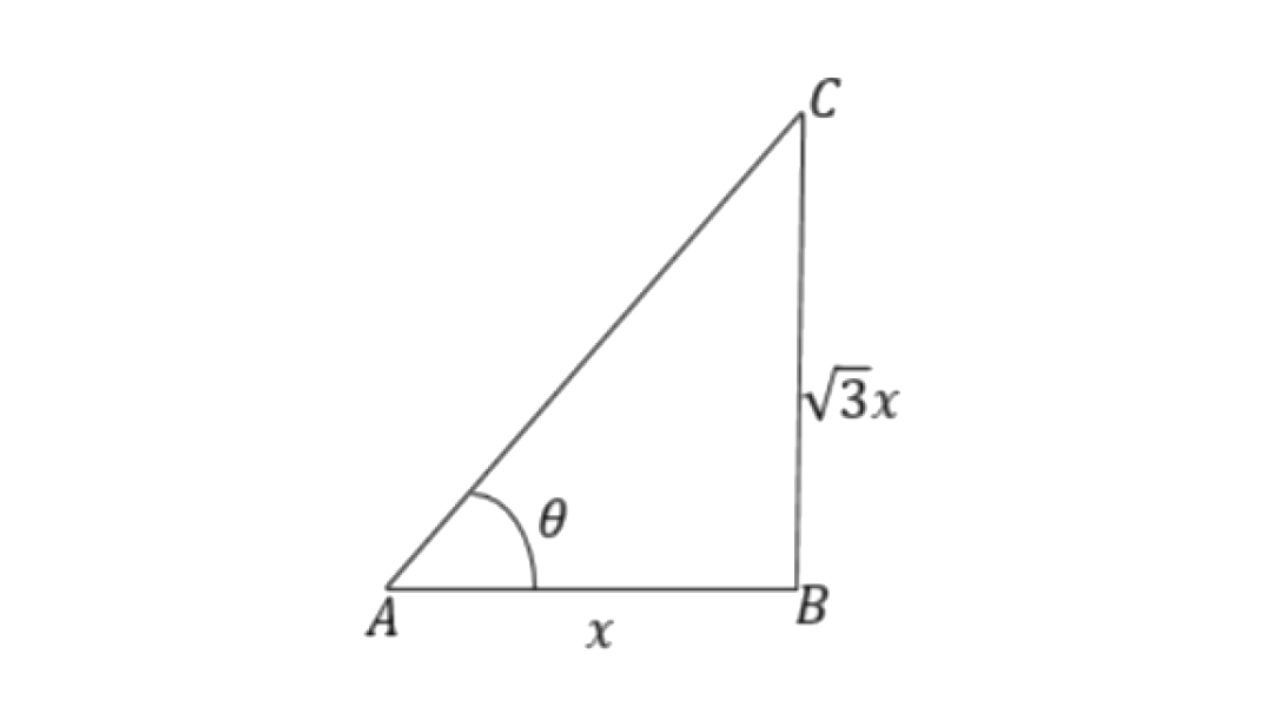
Here,
From
So, the angle of elevation is 60°.
2. The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower. tower.
Ans: Let the height of the tower be
The angle of elevation is 60°.
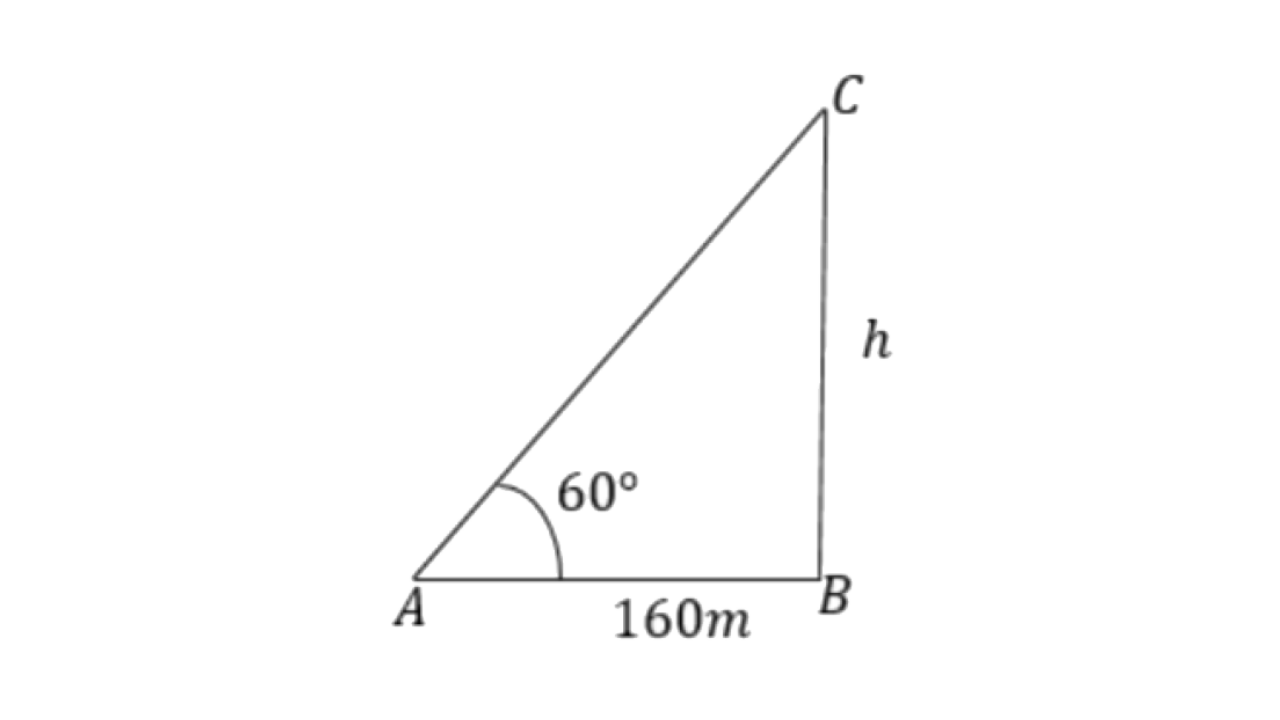
From
So, the height of the tower is 277.13m.
3. A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the reaches.
Ans: Let height upto which the ladder reaches be
The angle of elevation is 68°.
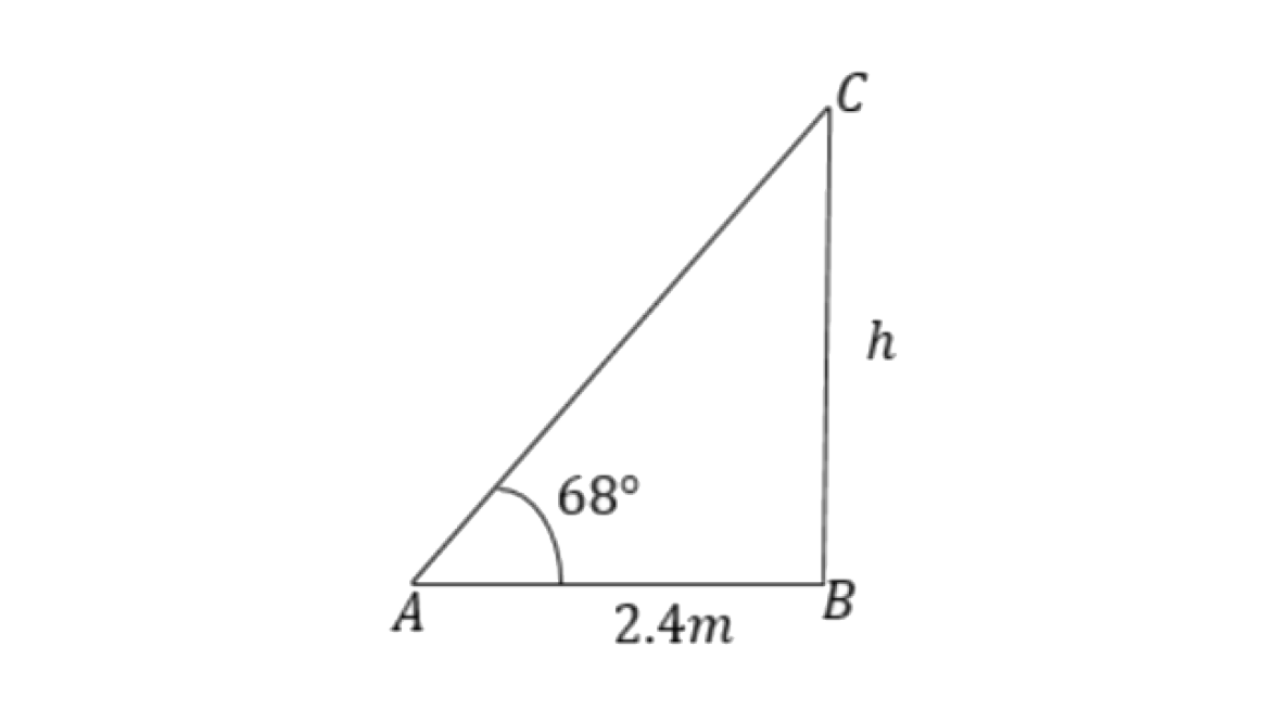
From
So, the height up to which the ladder reaches is 5.94m.
4. Two persons are standing on the opposite sides of the tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50m.
Ans: Let the distance between both the persons be
The angle of elevation of A is 30°.
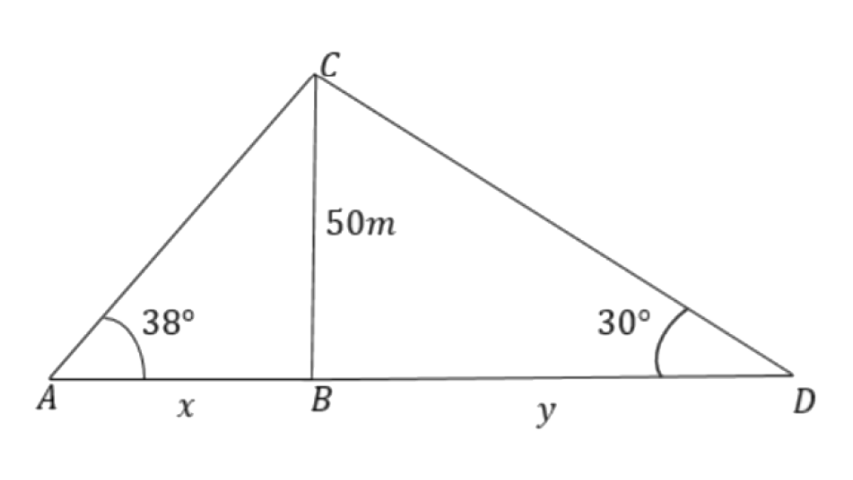
From triangle
From triangle
Therefore the distance between both the persons will be,
5. A kite is attached to a string. Find the length of the string, when the height of the kite is 60m and the string makes an angle 30° with the ground.
Ans: Let the length of the string be L.
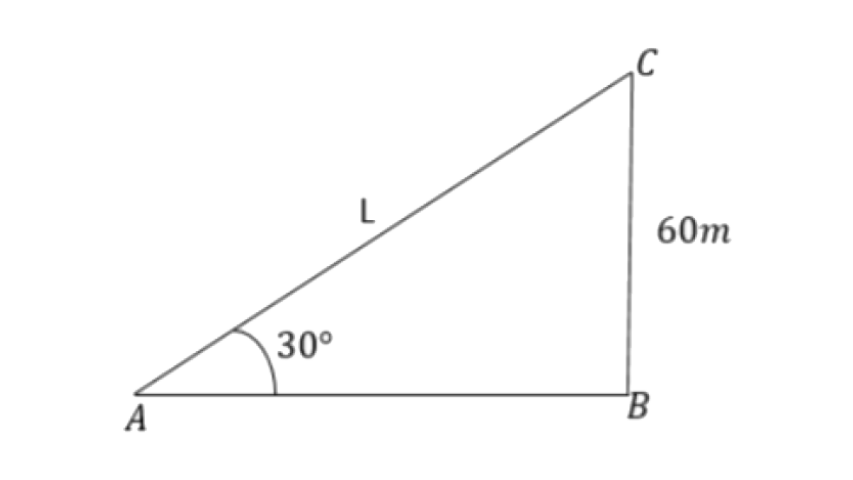
From triangle
So, the length of the string is 120m
6. A boy, l.6m tall, is 20m away from a tower and observes the angle of elevation on the top of the tower to be (i) 45° (ii) 60°. Find the height of the tower in each case.
Ans: Let the height of the tower be ‘
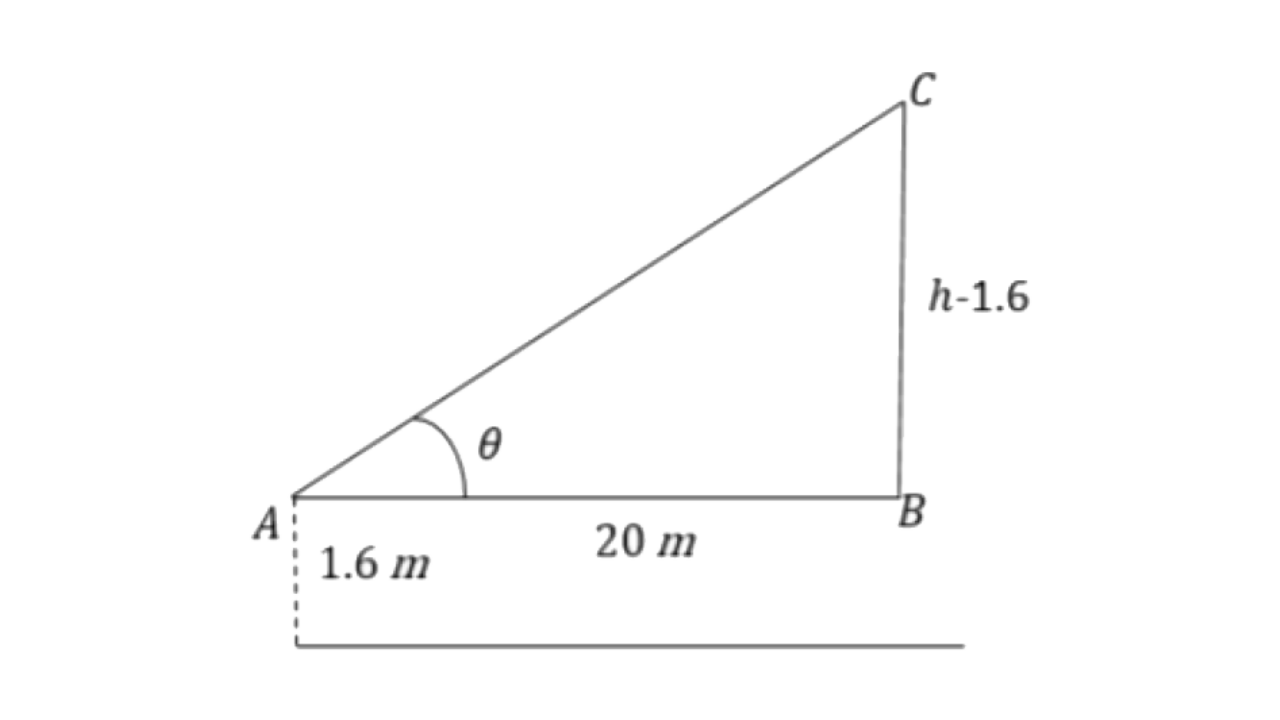
(i) If
From triangle
So, the height of the tower is 21.6m.
(ii) If
From triangle
So, the height of the tower is 36.24m.
7. The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground; and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
Ans: Let the height of the braking tree be ‘
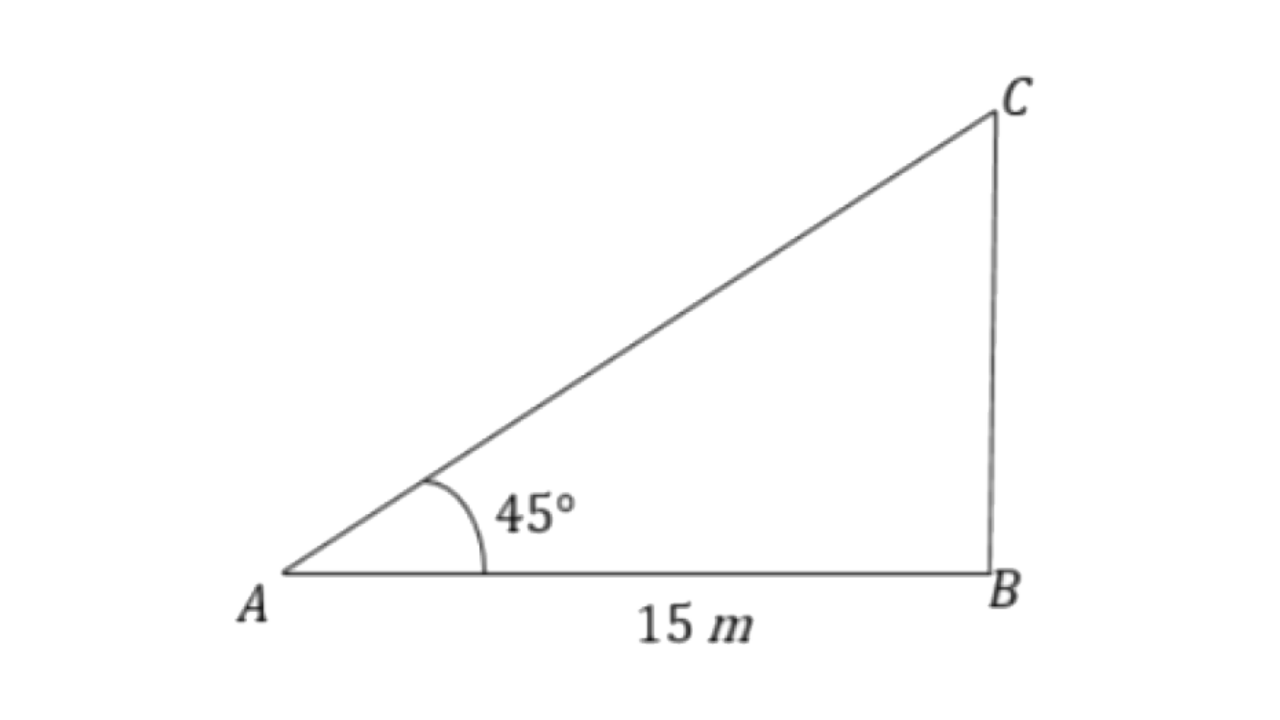
The angle of elevation is 45°.
The height of the tree before its braking is AC + BC
From triangle
Now, length of the tree broken by the wind,
So, the height of the tree before its braking is,
8. The angle of elevation of the top of an unfinished tower from a point at a distance of 80m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Ans: Let ‘
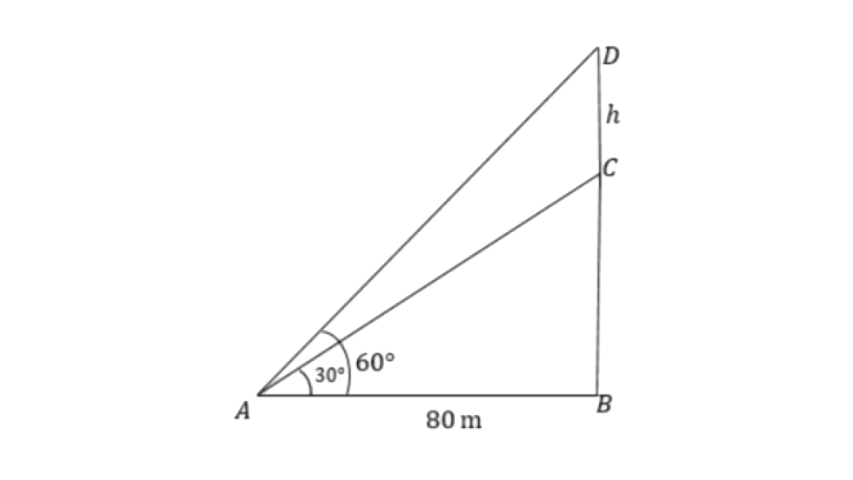
From triangle
From triangle
h = 92.376 m
Therefore the tower must be raised by 92.376m.
9. At a particular time, when the sun's altitude is 30°, the length of the shadow of a vertical tower is 45m. Calculate:
(1) the height of the tower,
(ii) the length of the shadow of the same tower, when the sun's altitude is :
(a) 45°
(b) 60°.
Ans: (i) Let ‘
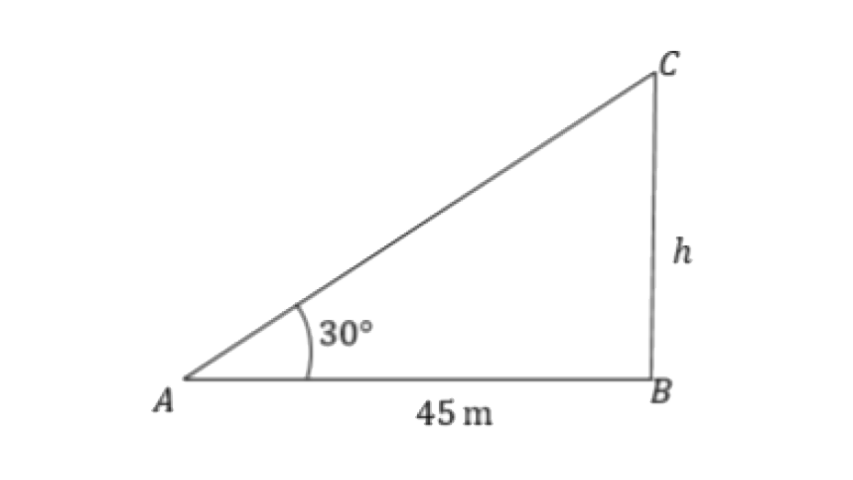
From triangle
(ii) Length of the shadow if θ =
Length of the shadow if θ = 60°,
So the length of the shadow is 15m.
10. Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes an angle 32°24' with the pole and when it is turned to rest against another pole. It makes an angle 32°24' with the road. Calculate the width of the road.
Ans:
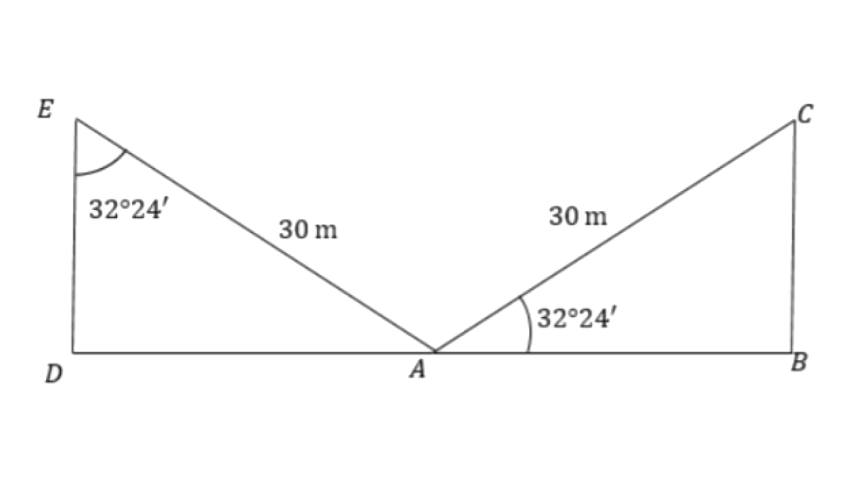
Here, the width of the road is DB.
From triangle
From triangle
Therefore, width of the road will be,
11. Two climbers are at points A and B on a vertical cliff face. To an observer C, 40m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
Ans: Let the distance between the climbers is ‘
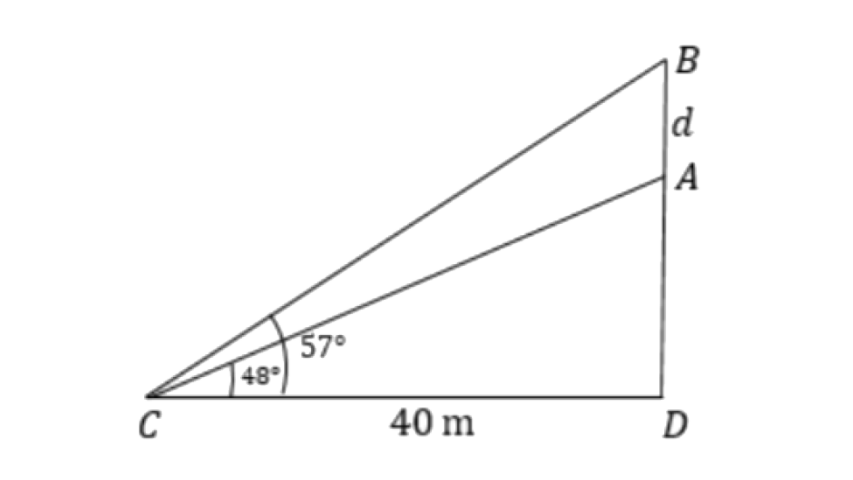
From triangle
From triangle
Therefore the distance between the climber will be,
12. A man stands 9m away from a flag-pole. He observes that the angle of elevation of the top of the pole is
Ans:
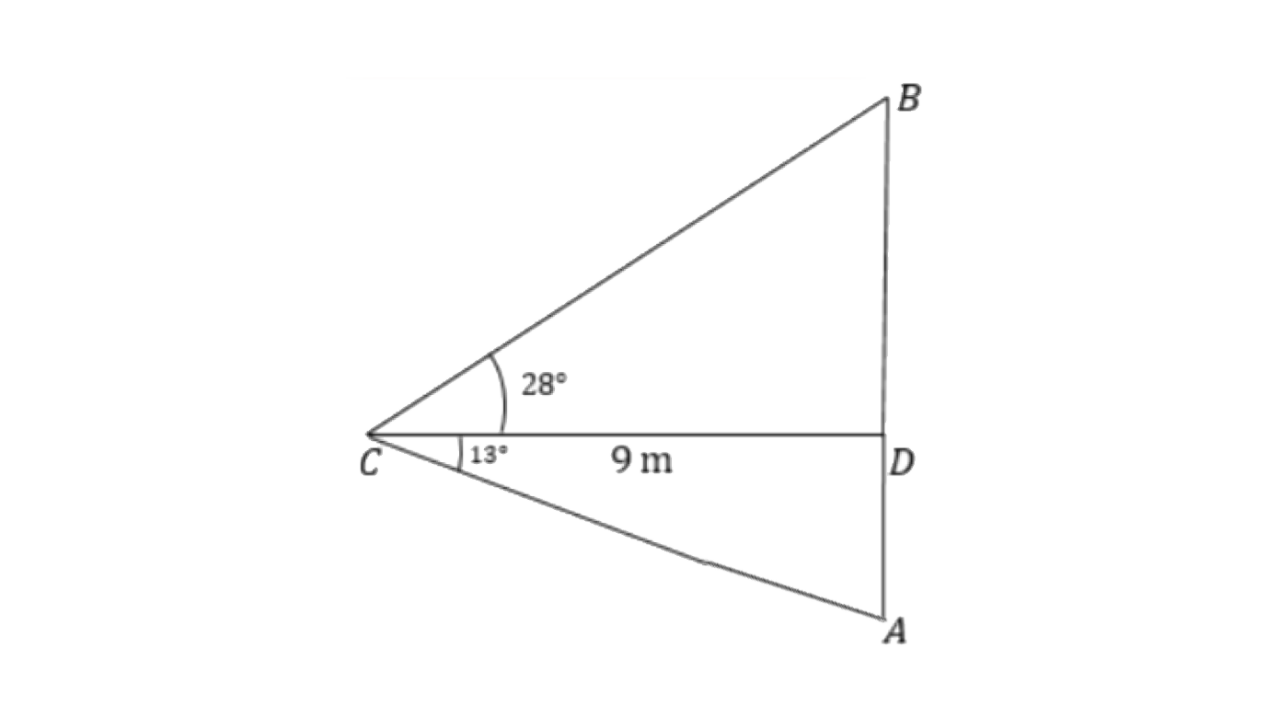
The length of the flag-pole will be BD + AD
From triangle
From triangle
Therefore the height of the flag-pole will be,
13. From the top of a cliff 92m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
Ans:
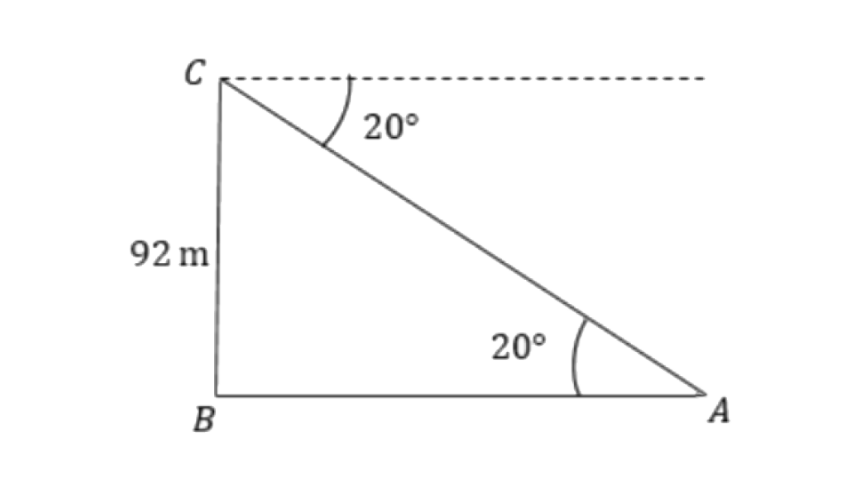
From triangle
So, the distance of the buoy from the foot of the cliff is 253.44m.
EXERCISE 22(B)
1. In the figure, given below, it is given that AB is perpendicular to BD and is of length X metres. DC = 30 m,
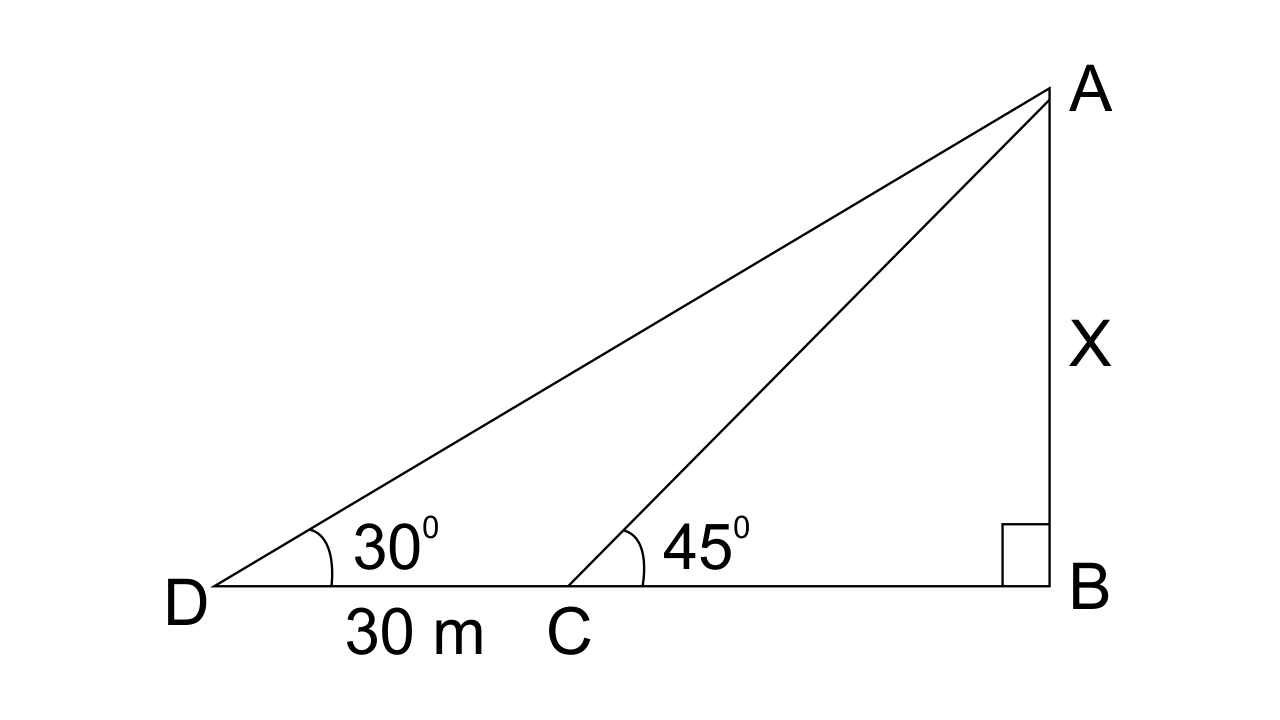
Ans: From triangle
From triangle
2. Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
Ans: Let the height of the tree be ‘
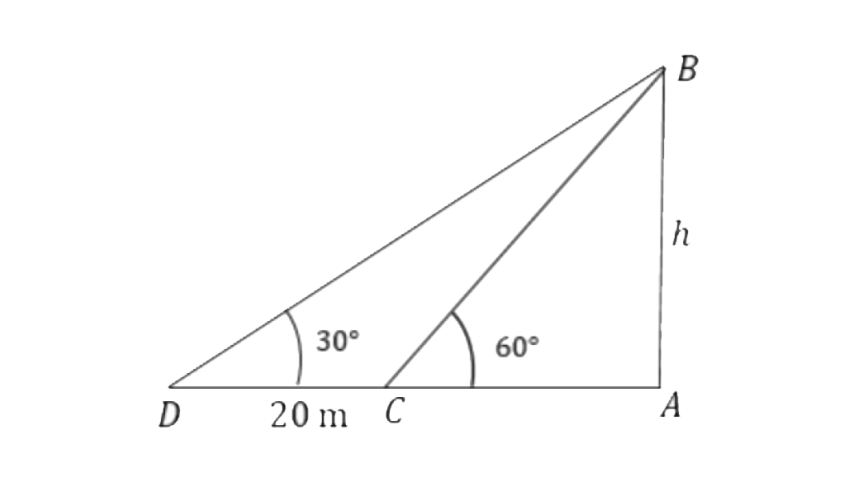
From triangle
From triangle
So, the height of the tree is 17.316m.
3. Find the height of a building, when it is found that on walking towards it 40m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
Ans: Let the height of the building is ‘
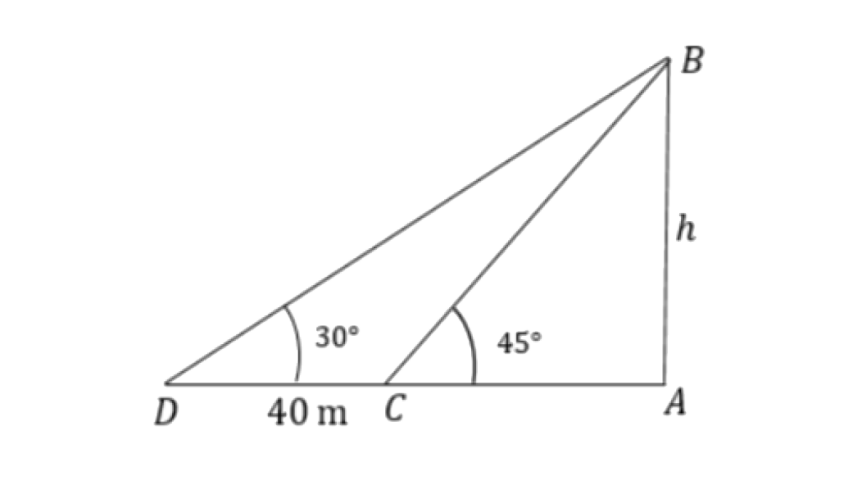
From triangle
From triangle
So, the height of the building is 54.64m.
4. From the top of a lighthouse 100m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if.
(i) the ships are on the same side of the light house,
Ans:
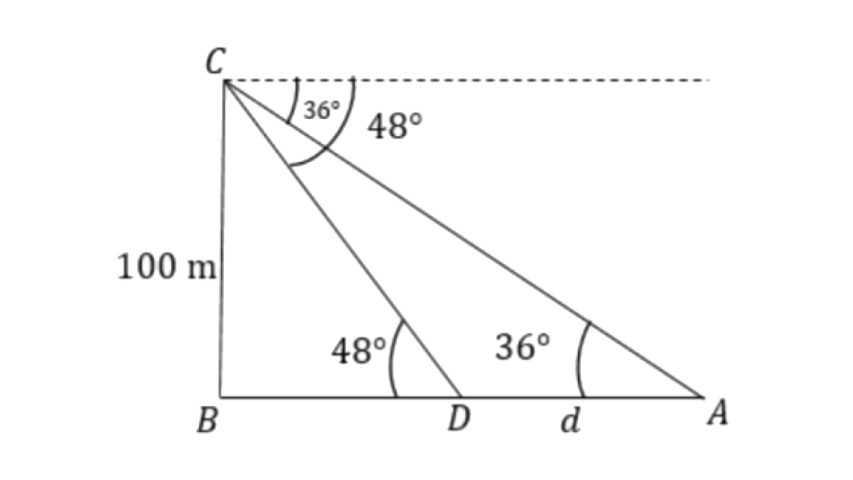
Let distance between the two ships is ‘
From triangle
From triangle
The distance between two ships will be,
(ii) the ships are on the opposite sides of the light house.
Ans:
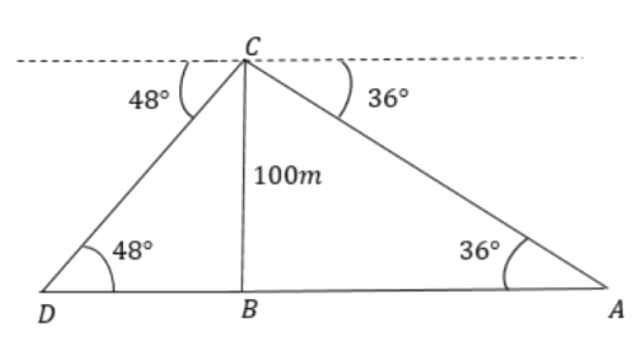
The distance between two ships will be,
5. Two pillars of equal heights stand on either side of a roadway, which is 150m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
Ans: Let the height of the pillar be ‘
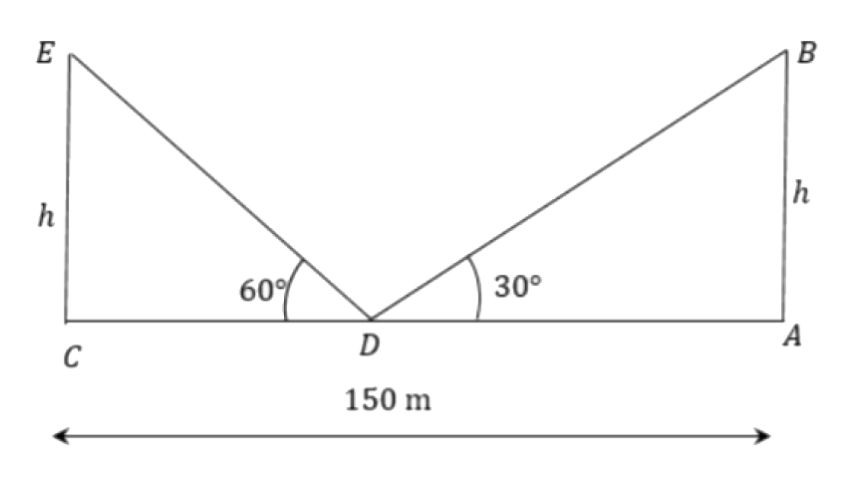
From triangle
From triangle
The width of the roadway is 150m.
Therefore
And the position of the point CD from pillar CE is,
6. From the figure, given below, calculate the length of the CD.
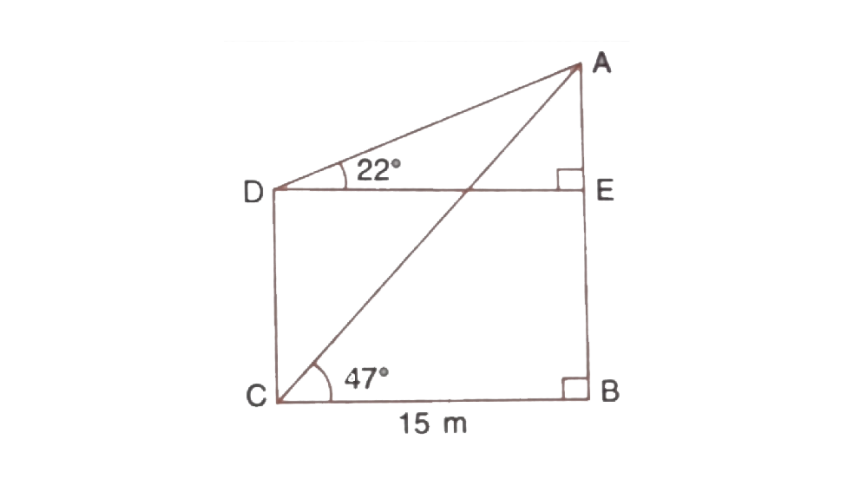
Ans: From triangle
From triangle
Length of CD is,
7. The angle of elevation of the top of a tower is observed to be 60°. At a point, 30m vertically above the first point of observation, the elevation is found to be 45°. Find :
(i) the height of the tower,
(ii) its horizontal distance from the points of observation.
Ans:
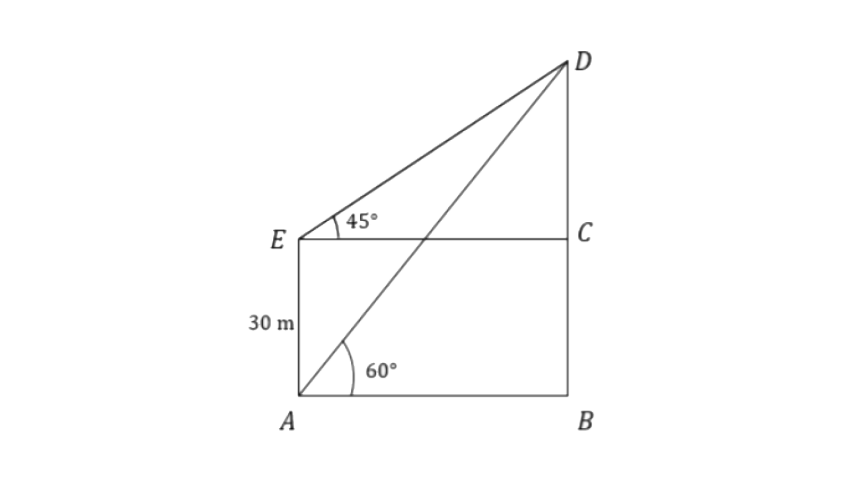
Let the height of the tower be ‘
From triangle
From triangle
Here AB = CE
Therefore,
Therefore, height of the tower is 70.92m
(ii) The horizontal distance from point of observation is,
8. From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Ans:
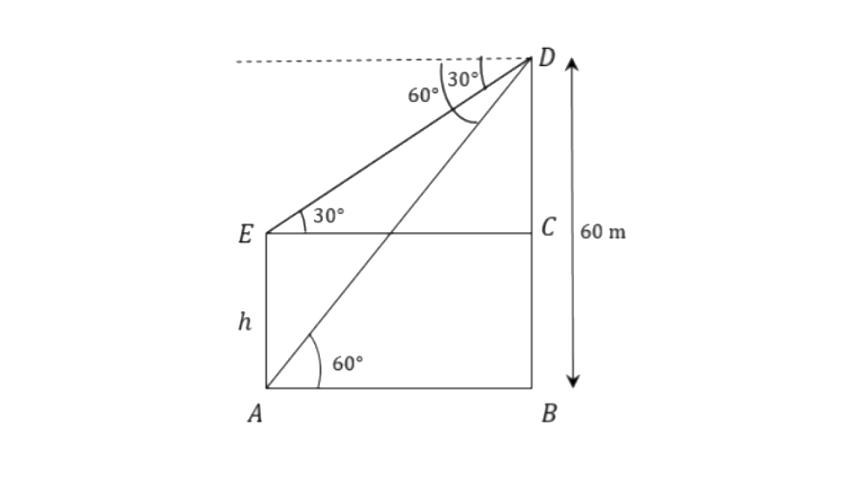
Let the height of the tower be ‘
From triangle
From triangle
Therefore AE = CB = DB - DC = 60 - 20 = 40m
Hence, the height of the tower is 40m.
9. A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat was found to be 60°. Assuming that the boat sails at a uniform speed, determine:
(i) how much more time will it take to reach the shore ?
(ii) the speed of the boat in meters per second, if the height of the cliff is 500 m.
Ans: Let the height of the cliff be ‘h’ and point A be the initial position and point D be the position of the boat after 3 min.
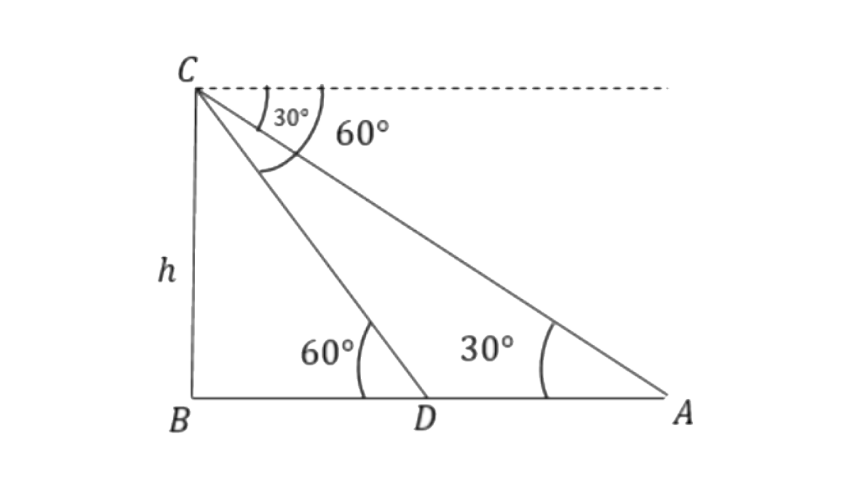
From triangle
From triangle
Speed of the boat will be,
Time taken by the boat to reach the shore is,
(ii) If h = 500m, then the speed of the boat will be,
As a result, the boat takes 1.5minutes longer to reach the shore. And, if the cliff is 500metres high, the boat's speed is 3.21metres per second.
10. A man in a boat rowing away from a lighthouse 150m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
Ans: Let BC be the lighthouse, point D be the initial position and point A be the final position of the boat after 2min.
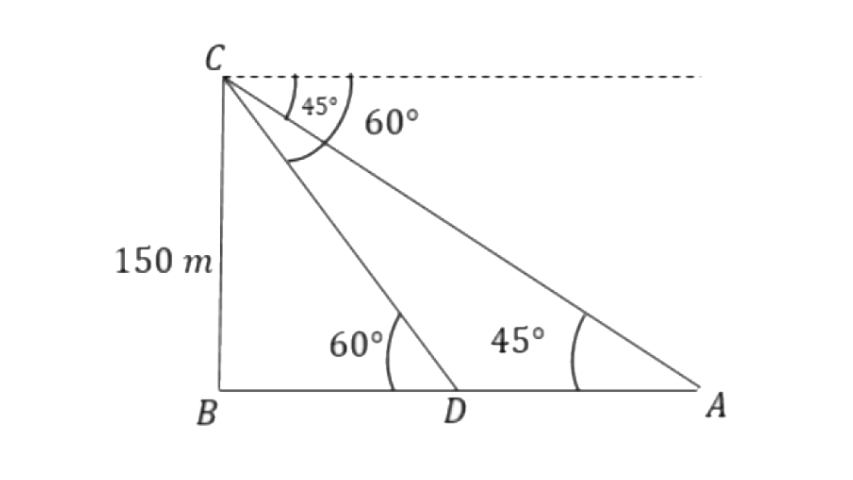
From triangle
From triangle
Speed of the boat will be,
Hence, speed of the boat is 0.528m/s
11. A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40m away from the bank, he finds the angle of elevation to be 30°. Find:
(i) the height of the tree, correct to 2 decimal places,
(ii) the width of the river.
Ans:
Let the height of the tree be ‘h’, point A be the initial position, point D be the final position of the person and AC be the width of the river.
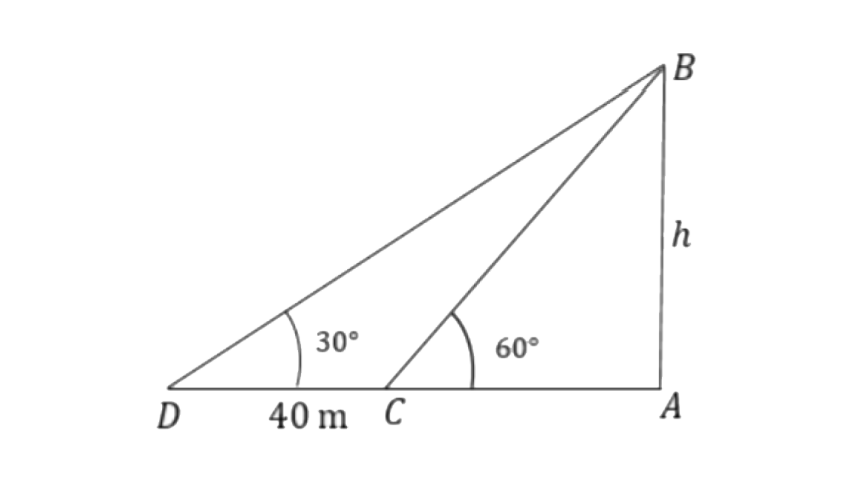
From triangle
From triangle
Therefore, the height of the tree is 34.64m
Width of the river is AC,
As a result, the height of the tree is 34.64m and the width of the river is 20m.
12. The horizontal distance between two towers is 75m and the angular depression of the top of the first tower as seen from the top of the second, which is 160m high, is 45°. Find the height of the first tower.
Ans: Let the height of the first tower is ‘
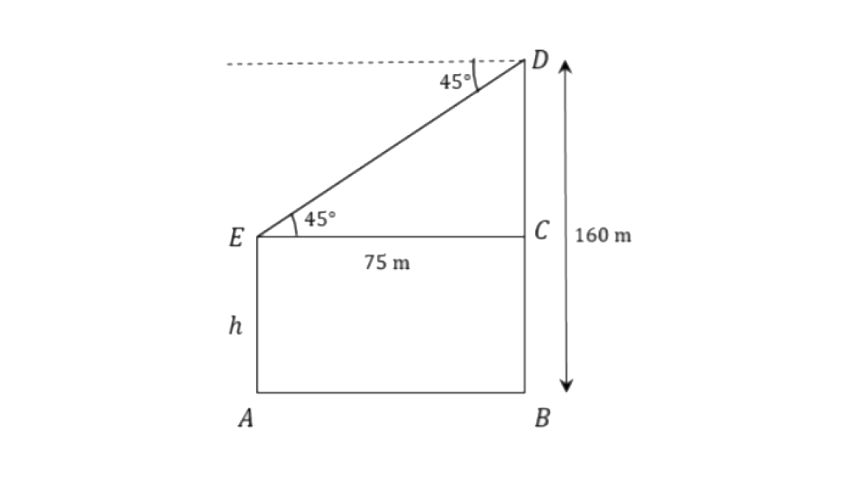
From triangle
The height of the first tower is,
13. The length of the shadow of a tower standing on a level plane is found to be 2y metres longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is
Ans: Let AB is the tower of height ‘
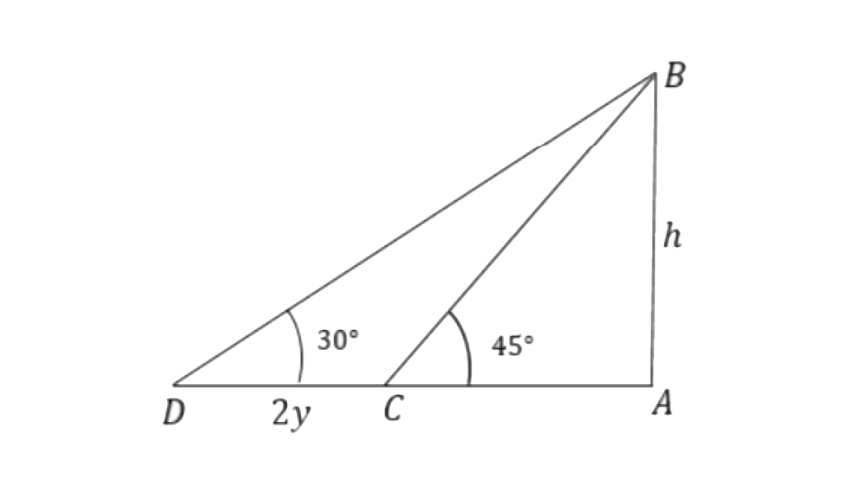
From triangle
From triangle
Here AC = AB, thus
On rationalising the RHS by multiplying numerator and denominator with
Hence proved.
14. An aeroplane flying horizontally 1km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
Ans: Let the initial position of the aeroplane be D and final position be C.
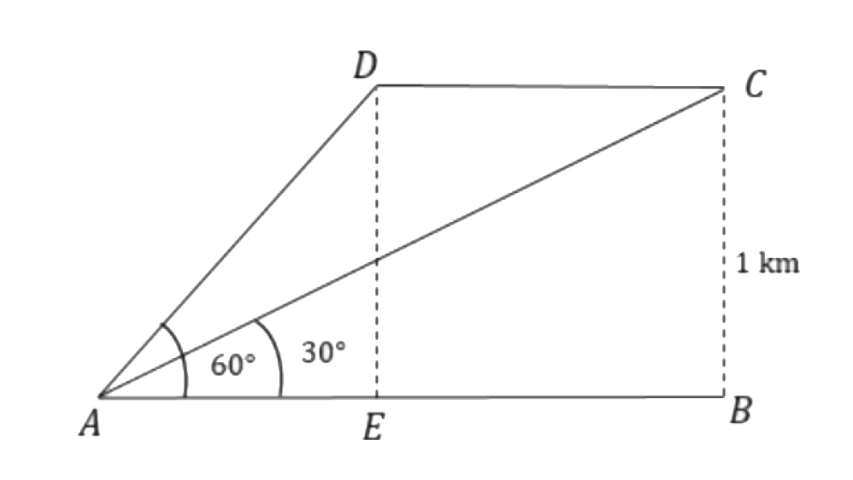
From triangle
From triangle
The speed of the aeroplane will be,
15. From the top of a hill, the angles of depression of two consecutive kilometre stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Ans: Let's assume the hill's height is ‘h’, and the stones are shown at points D and A.
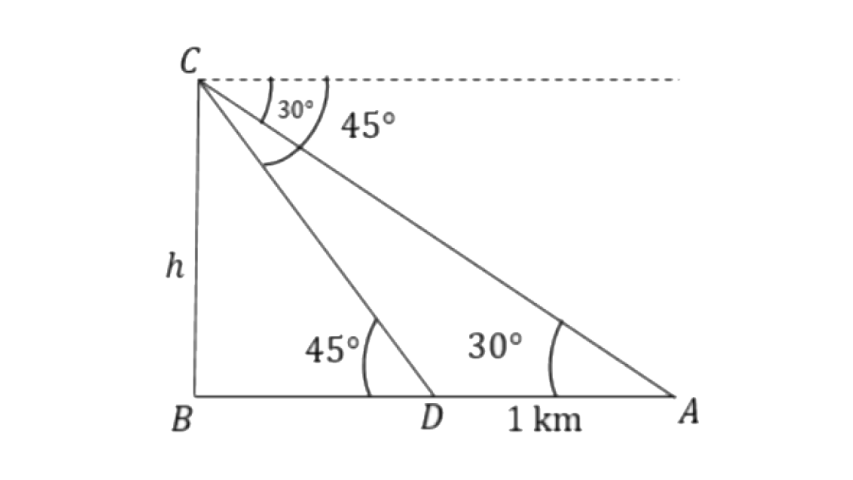
From triangle
From triangle
Here,
The distance between stone at point D and foot of hill is,
The distance between stone at point A and foot of hill is,
EXERCISE 22(C)
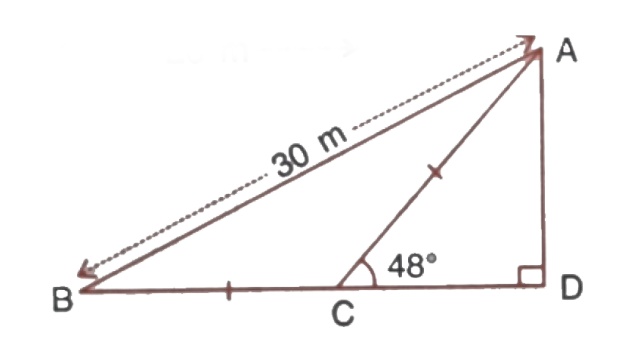
1. Find AD,
(i)
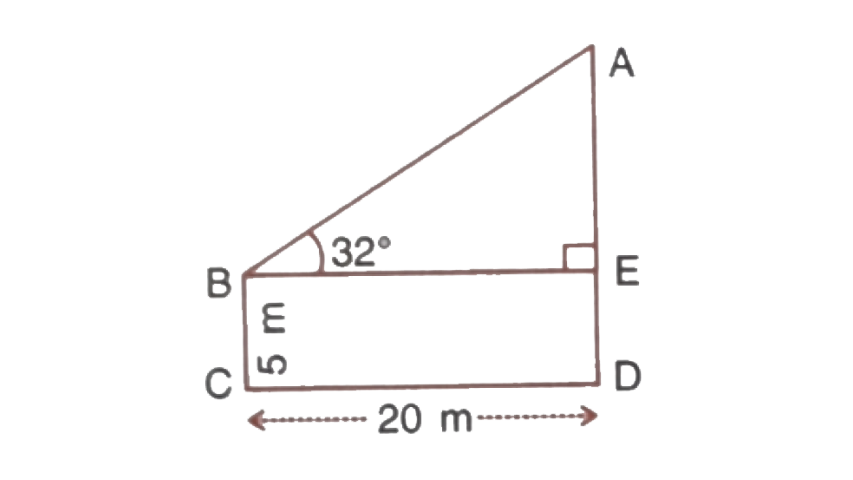
(ii)
Ans: (i) From triangle
And,
(ii) From triangle
And,
By pythagoras theorem we get,
2. In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1m and
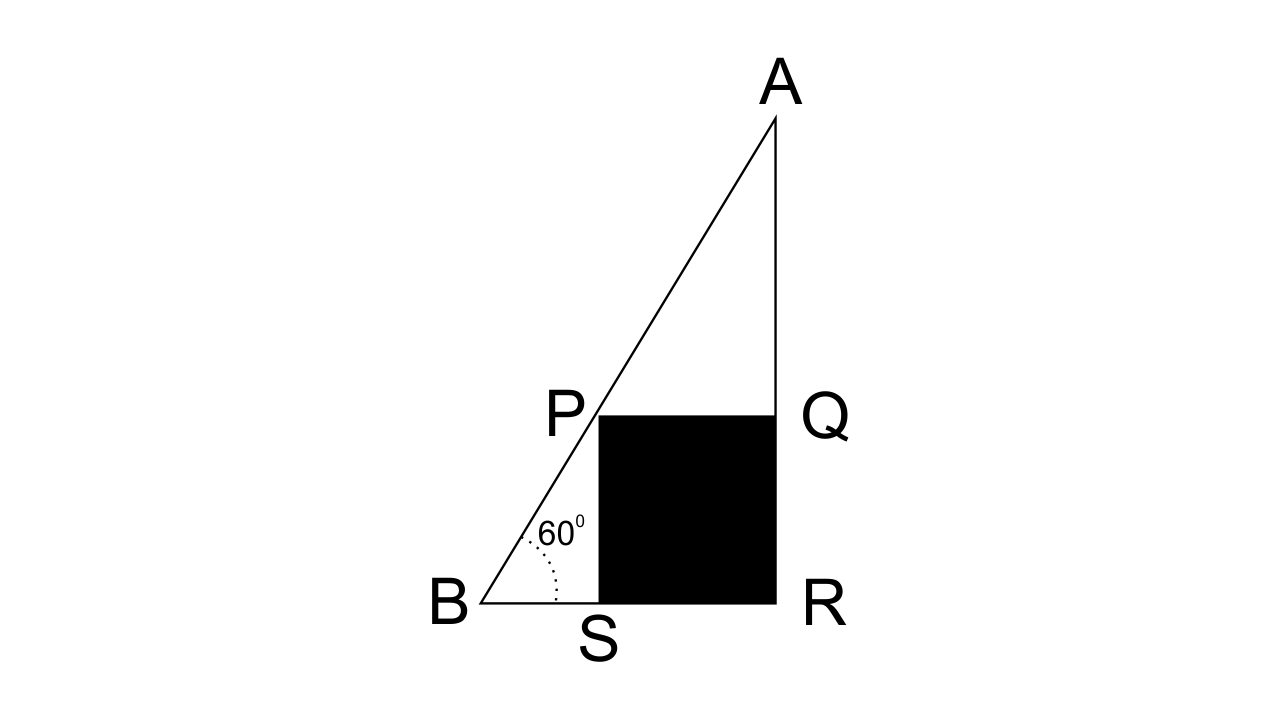
Ans: The block is cubical. Therefore, PS = PQ = 1m.
From triangle
From triangle
Length board AB is,
3. Calculate BC.
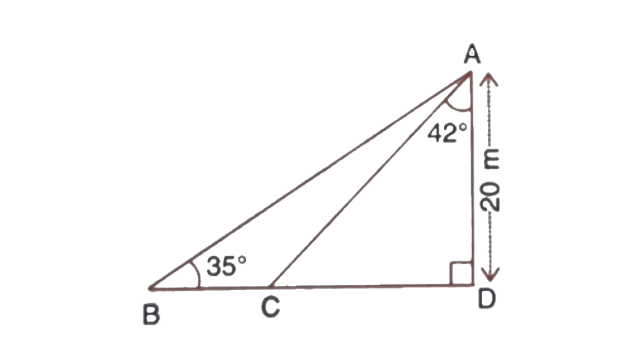
Ans: From triangle
From triangle
Length of BC will be,
4. Calculate AB.
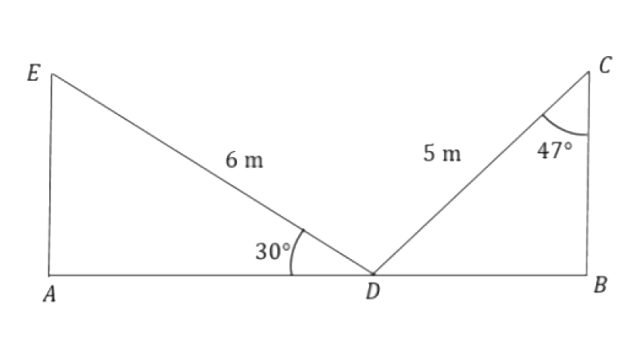
Ans: From triangle
From triangle
Length of AB will be,
5. The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry calculate,
(i) the length of AB
(ii) the distance of AB from the centre C.
Ans:
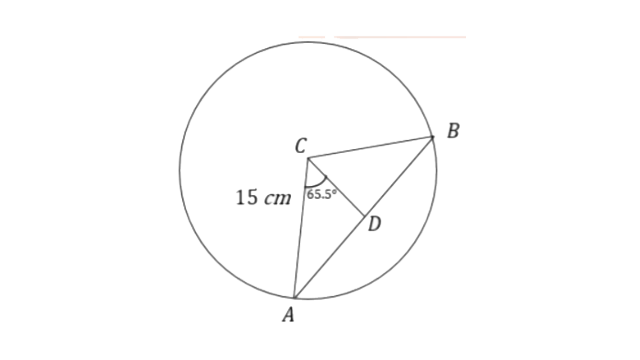
(i) Here, AD = DB
Therefore, length of the chord is,
AB = 2AD
From triangle
Therefore AB will be,
(ii) The distance of the chord from the center will be CD.
From triangle
6. At a point on level ground, the angle of elevation of a vertical tower is found to be such 5 that its tangent is
Ans: Let the height of the tower be ‘
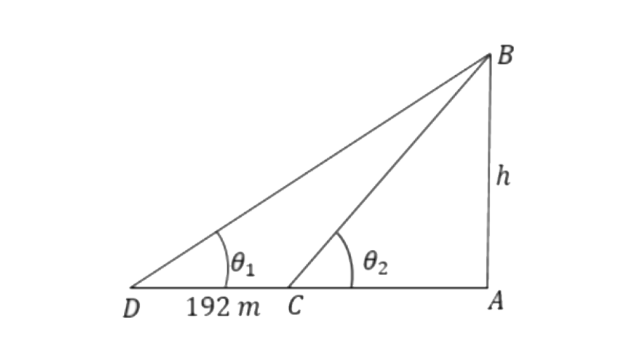
Point D is the initial position and point C is the final position.
From triangle
From triangle
And,
So, the height of the tower is 180m.
7. A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is a and that of the top of the flagstaff is
Ans: Let CD be the flagstaff and BC be the height of the tower.
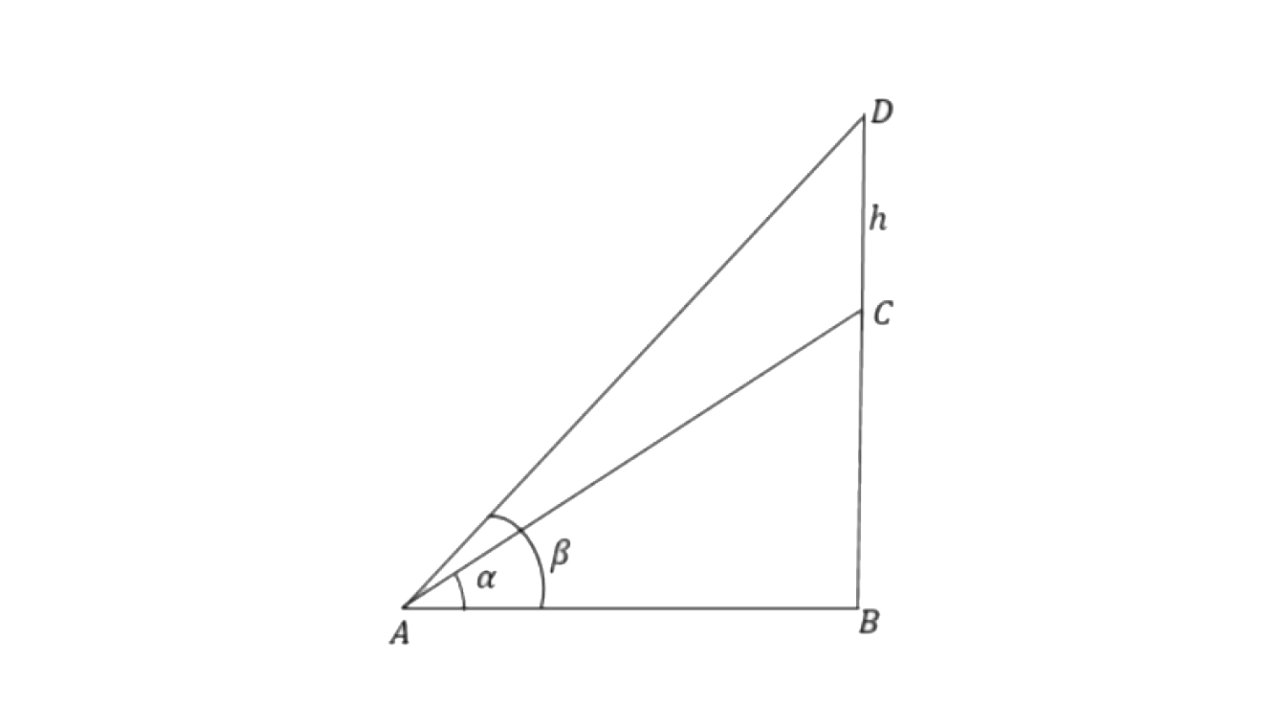
From triangle
From triangle
Hence proved
8. With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° =
(i) the distance AB in metres;
(ii) angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
Ans: Let BC be the height of the pole and tan x° =
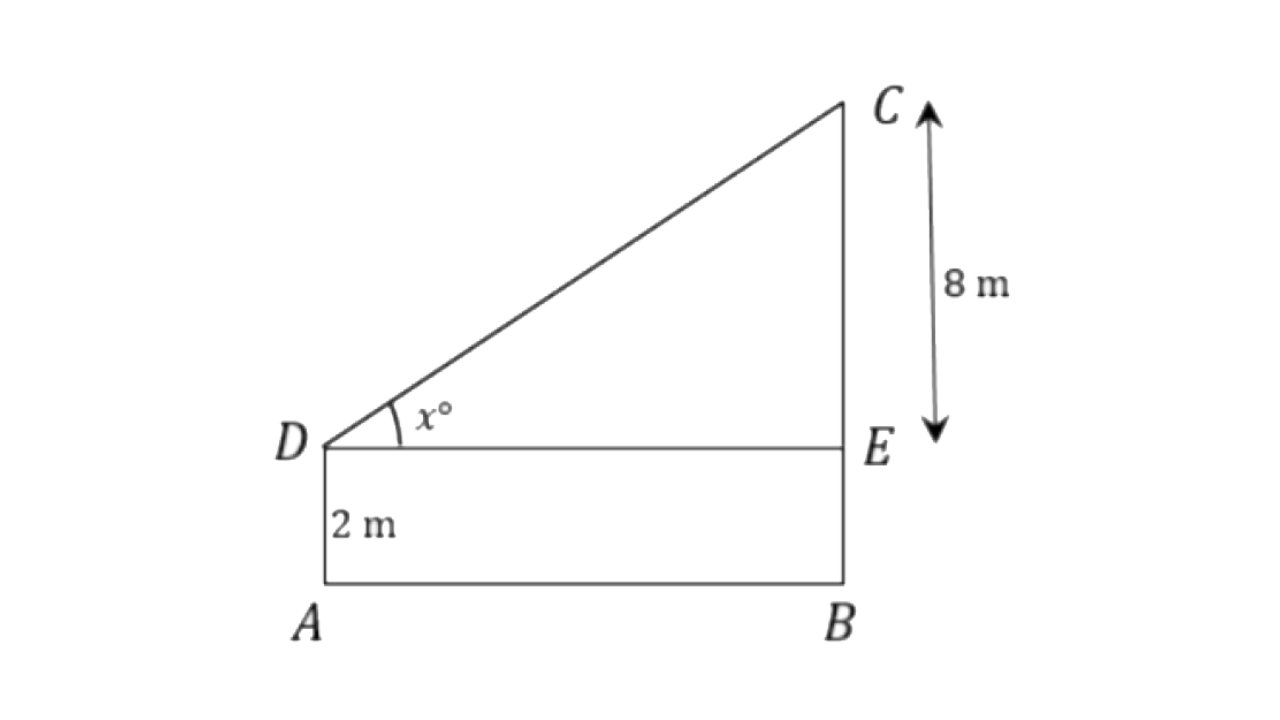
(i) From triangle
Here AB = DE = 20m
(ii)
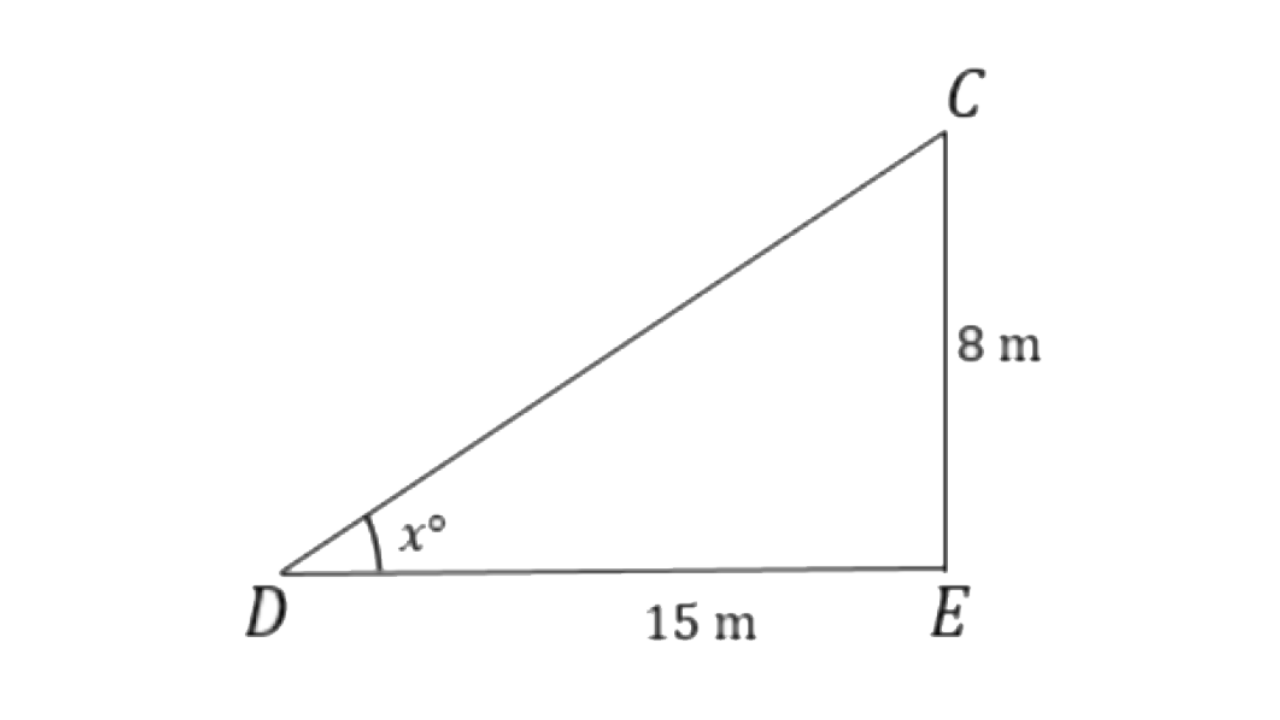
From triangle
9. The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is
Ans: Let the height of the tower be ‘
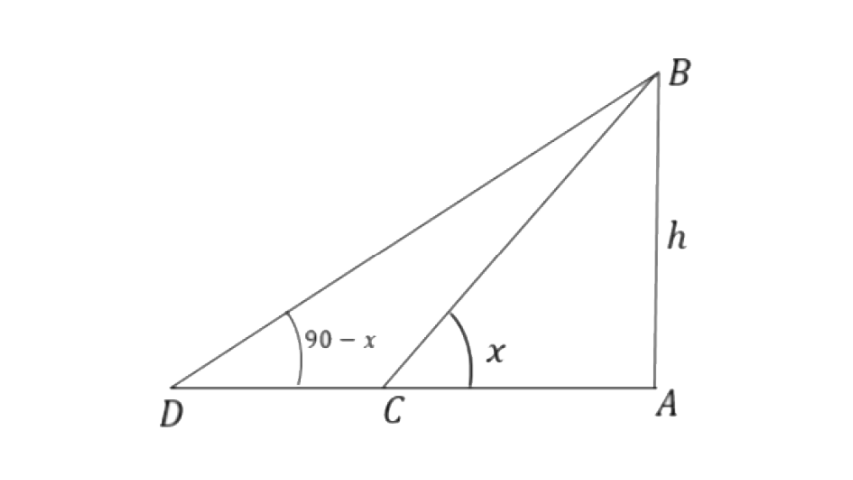
Given, AC = a and AD = b.
From triangle
From triangle
Hence proved
10. From a window A, 10m above the ground the angle of elevation of the top C of a tower is x°, where tan x° =
Ans:
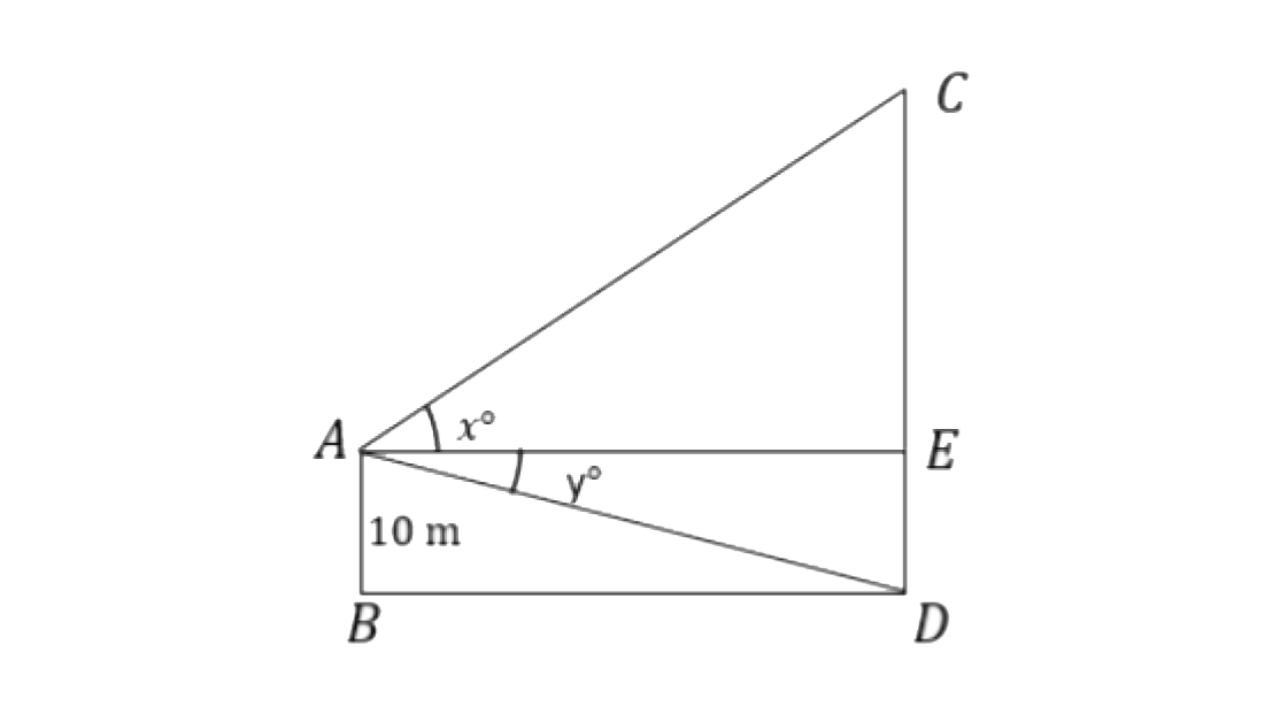
Here AB = ED = 10m
In triangle
W.K.T,
Therefore,
In triangle
W.K.T,
Therefore,
Therefore, the height of the tower is 110m.
11. A vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
Ans:
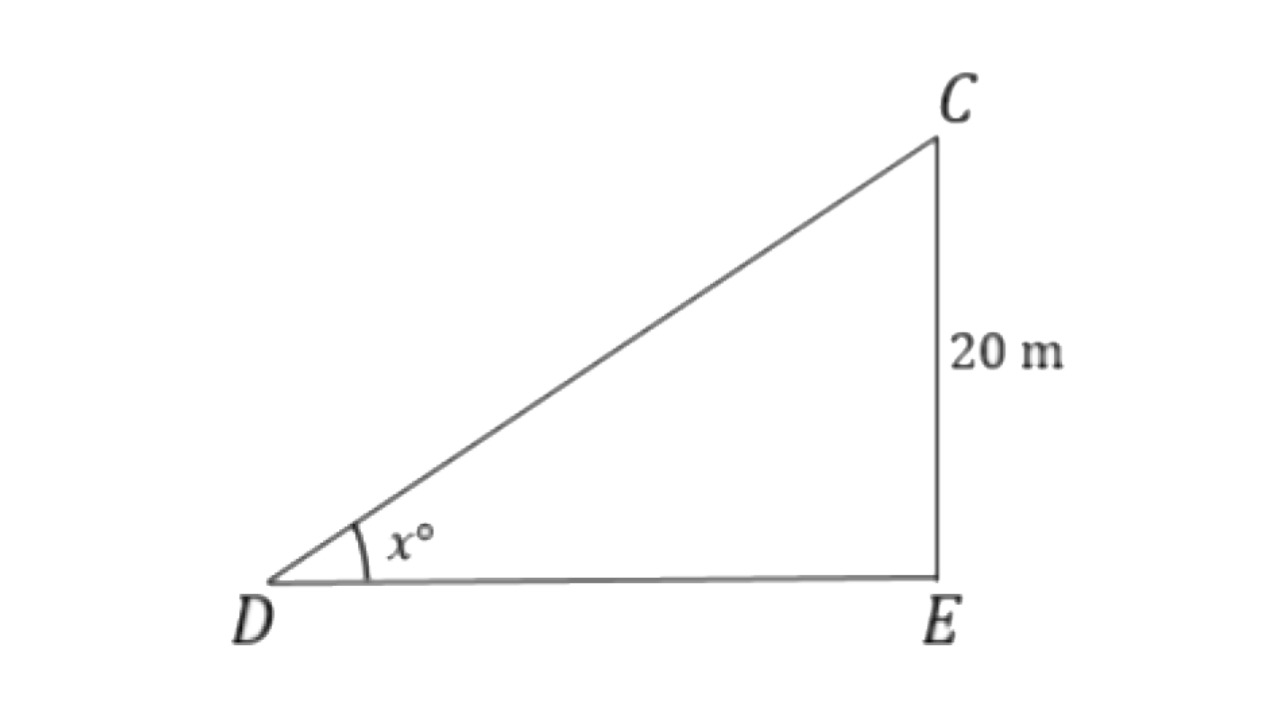
Height of the tower is 20m.
Let
Given
So from the triangle
12. A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50m away from the bank, he finds the angle of elevation to be 30°. Calculate:
(i) the width of the river and
(ii) the height of the tree.
Ans: The width of the river is AC and height of the tree is AB.
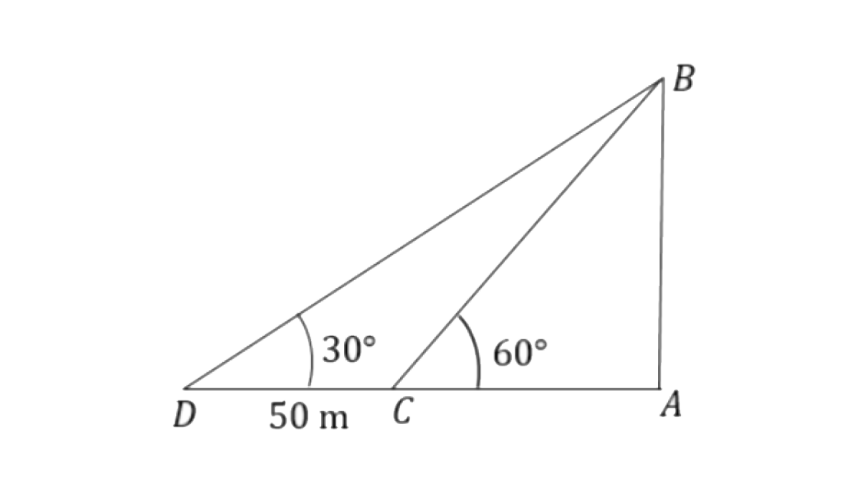
(i) From triangle
From triangle
W.K.T
So, the width of the river is 25m.
(ii) The height of the tree will be,
13. A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole as seen from the foot of the tower is 30°. Find:
(i) the height of the tower.
(ii) the horizontal distance between the pole and the tower.
Ans: Let the height of the pole is BD and the tower is AC.
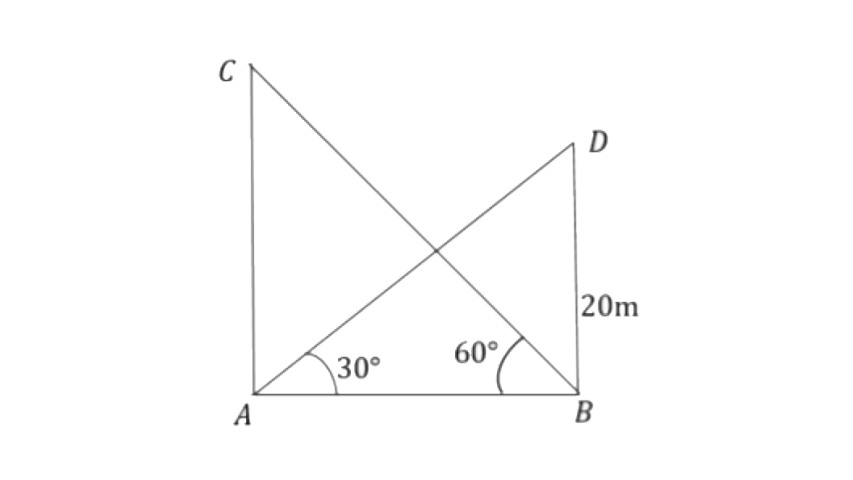
(i) From triangle
From triangle
Therefore
(ii) The horizontal distance between the pole and the tower is,
14. A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
(i) the height of the tower, if the height of the pole is 20m;
(ii) the height of the Pole, if the height of the tower is 75m.
Ans: Let AB be the pole and CD is the tower.
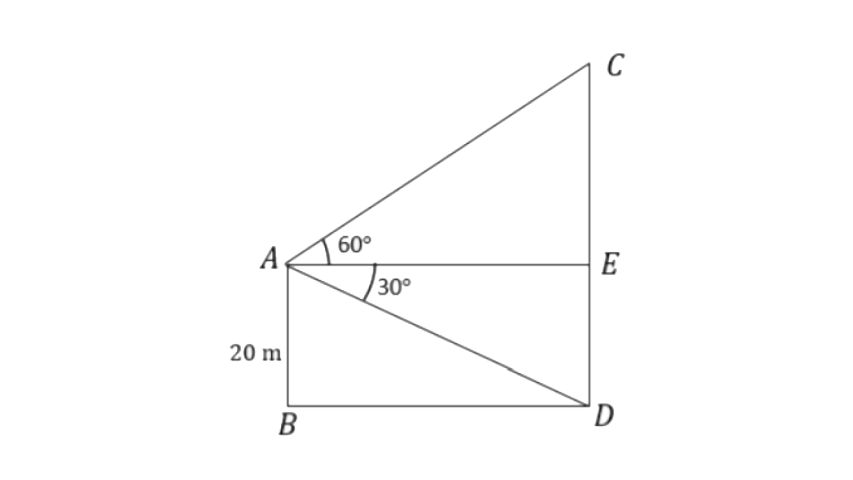
From triangle
From triangle
So, the height of the tower will be,
(ii)
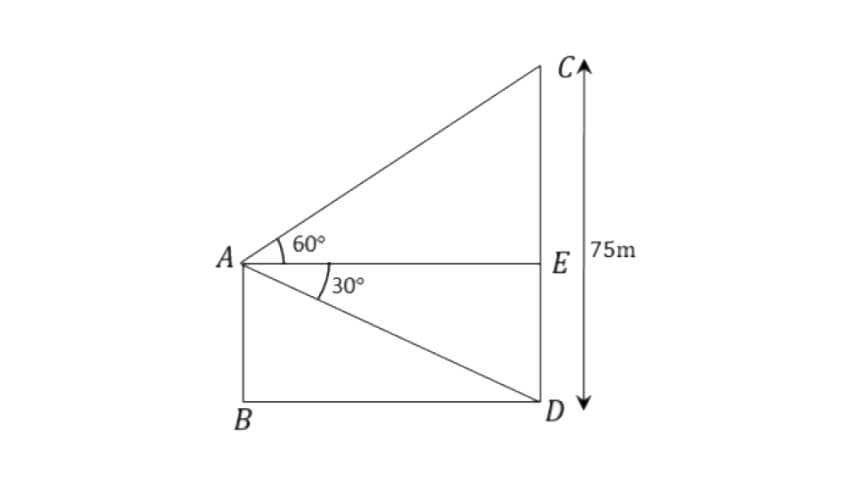
Here, AB = ED.
From triangle
From triangle ∆AEC,
So, the height of the pole will be,
15. From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Ans:
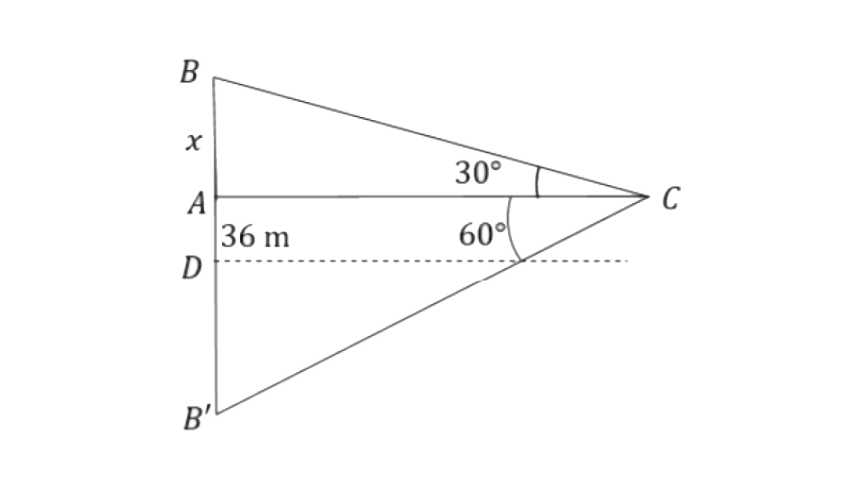
Let point B represent the bird's actual position, and point D represent the lake's surface.
So,
From triangle
From triangle
So, actual position of the bird is,
16. A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
Ans: Let the height of the building be AB. Pont D be the initial position and point C be the final position of the man.
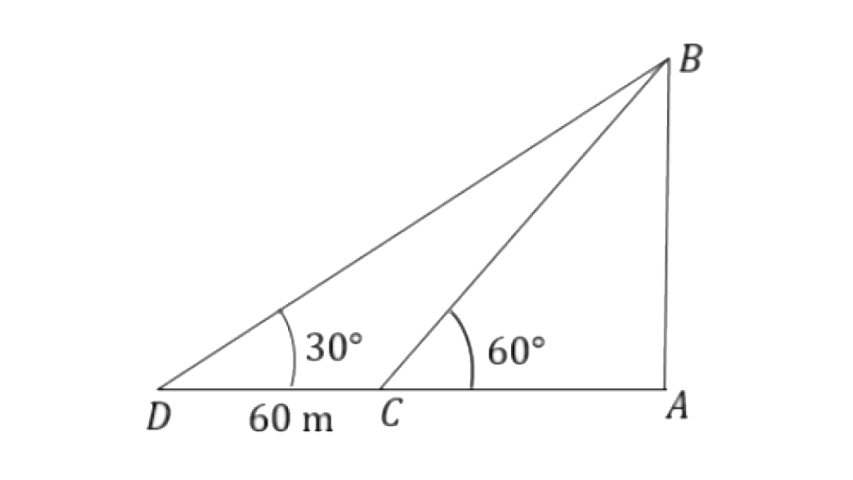
From triangle
From triangle
W.K.T, AD = AC + CD
So,
So the height of the building is 52m.
17. As observed from the top of a 80m tall lighthouse, the angles of depression of two ships, on the same side of the light house in horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer correct to the nearest metre.
Ans:
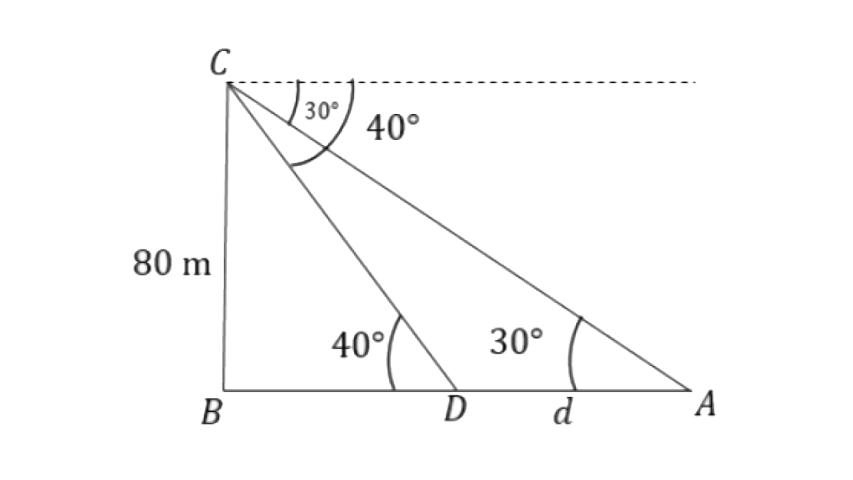
Let BC be the lighthouse and ‘
From triangle
From triangle
So the distance between the ships is 43m.
18.In the given figure, from the top of a building AB = 60m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find :
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
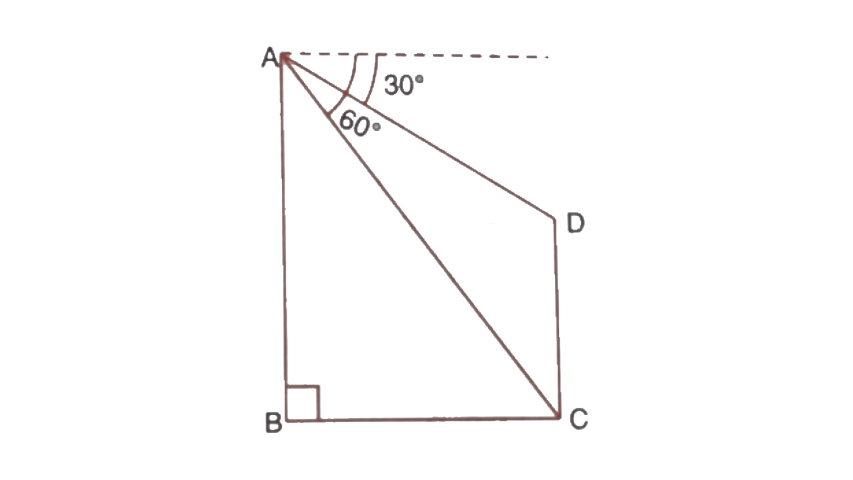
Ans: Here, AB = 60m and BC = ED
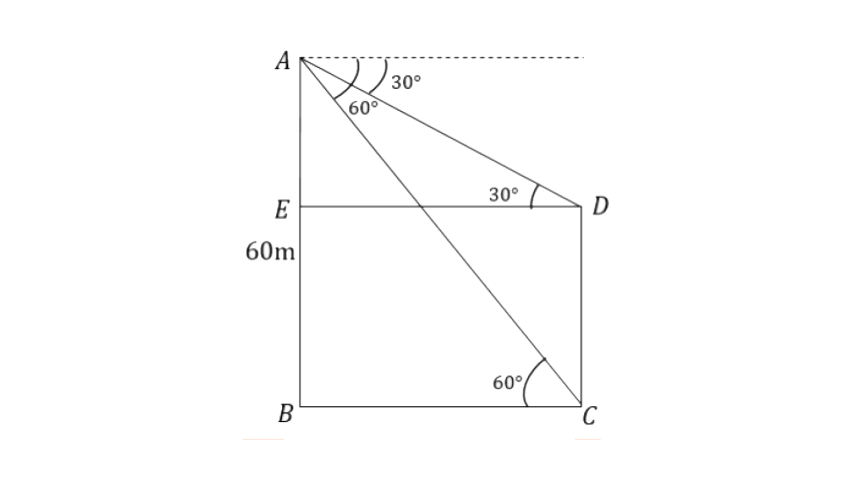
(i) From triangle
So, the horizontal distance between AB and CD is 34.64m.
(ii) From triangle
Therefore the height of the lamp post will be,
19. An aeroplane, at an altitude of 250m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
Ans:
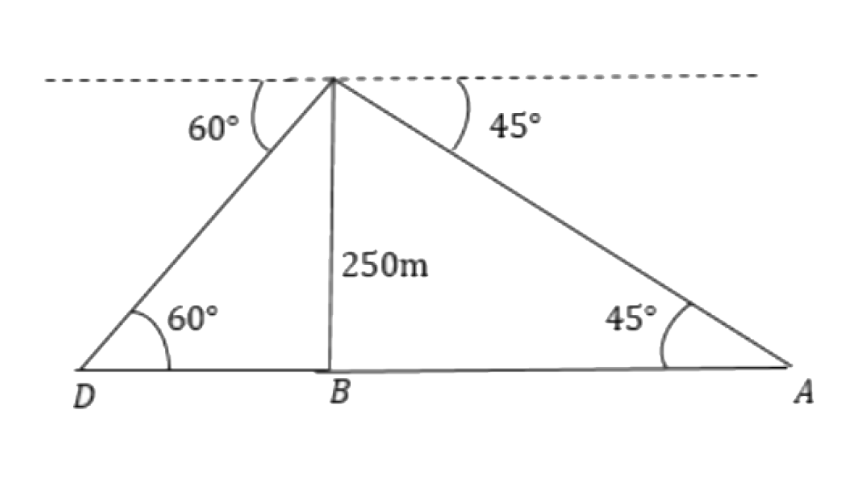
Let point C be the position of the aeroplane and point A and D be the position of the ships.
So the width of the river will be AD.
From triangle
From triangle
The width of the river will be
20. The horizontal distance between two towers is 120m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the tower is 30° and 24° respectively. Find the height of the two towers. Give your answer correct to 3 significant figures.
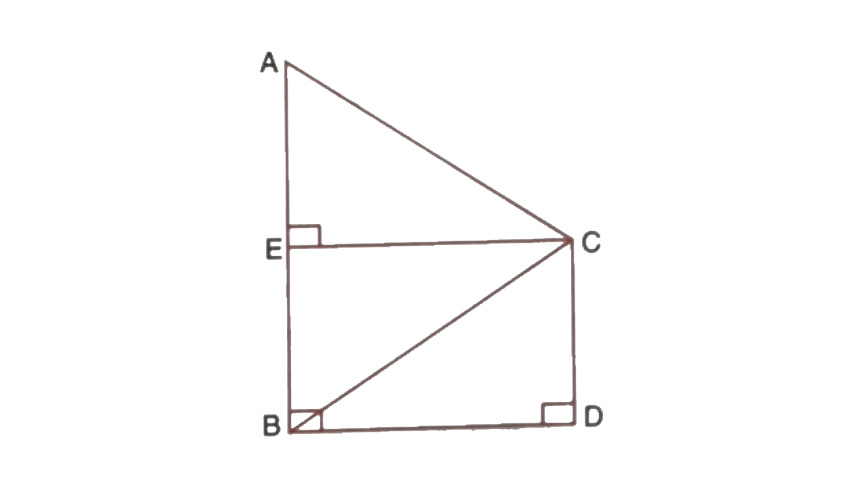
Ans: Let AB and CD be the towers.
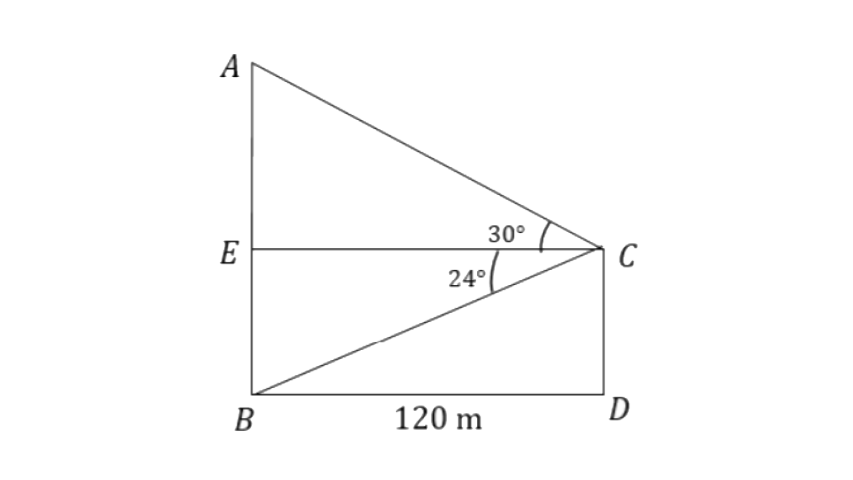
Here, BD = EC and BE = CD.
From triangle
The height of tower CD will be,
From triangle
The height of tower AB will be,
21. The angles of depression of two ships A and B as observed from the top of a lighthouse 60m high, are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
Ans: Let BC be the lighthouse and point A and point D be the position of the ships.
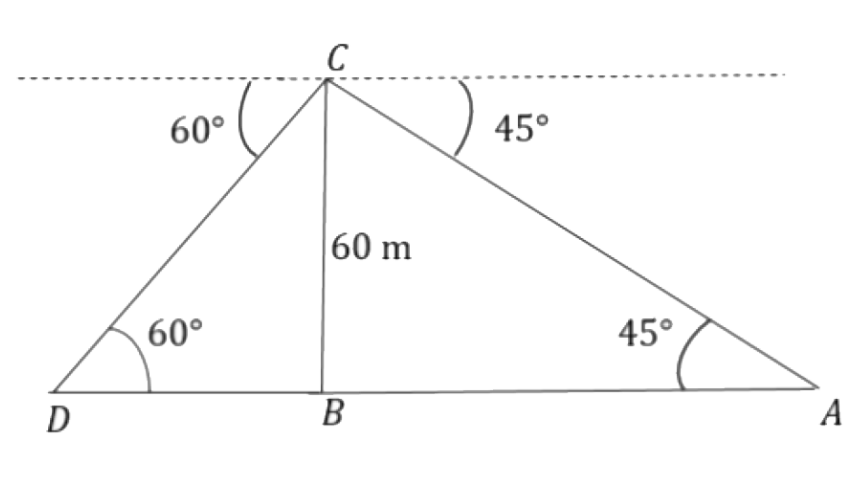
From triangle
From triangle
The distance between the ships will be,
Download ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions Free PDF
ICSE Class 10 Mathematics Chapter 22 Concise Solutions given on this page are solved by the Mathematician experts of Vedantu to help students in their studies. Our subject experts have precisely solved each question in a stepwise method considering the latest exam trend, and syllabus issued by the board. If you require a guide or an aid to your ICSE Class 12 Mathematics Chapter 22 preparation, and aren't sure how capable you are to solve the questions independently, then these Class 12 Mathematics Chapter 22 Selina Concise solutions offered by Vedantu will help you to prepare the chapter deliberately.
You can download ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions free PDF with a single click on the link provided.
Benefits of Referring to Concise Mathematics Class 10 ICSE Solutions for Chapter 22 Height and Distance By Vedantu
Here are some of the solid reason why you should refer to ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions by Vedantu:
The solutions are prepared by the Mathematician experts as per the latest ICSE syllabus and patterns that provide an additional benefit to your preparation level.
Solving these solutions will not only be helpful for you to score good grades in the Class 10 Mathematics exam but also prepares you for competitive exams like JEE Main, Maths Olympiad, etc.
The language used to solve the question is quite easy and thus facilitates the students to get through with the topics covered in the chapter in a better way.
Students can refer to the ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions free of cost and immediately resolve every doubt related to the chapter.
Relevant diagrams are also provided to help students to visualize and understand the question and solution in a better way.
Now, you must have understood how beneficial it is to refer to ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions. Apart from these, there are plenty of other benefits that you can explore by downloading Concise Mathematics Class 10 ICSE Solutions for Chapter 22 Height and Distance.
What Questions can be expected from Chapter 22 in Class 10 ICSE Board Exams?
ICSE Class 10 Chapter 22 titled as the Heights and distances is an important topic from the perspective of board exams. The chapter is quite interesting and fun. There can be many direct questions that can be expected from this topic. But of course, not the exact same questions but the same type. Students need preparation for this topic as it requires concentration on the part of the students. Therefore, students should practice as much as possible and make sure not to skip revision of the chapter when the exam approaches near. Since, there will be many direct questions that could be asked from this topic, students must keep revising the topic.
Most of the problems use a similar formula. There will be four different formulae in this concept at maximum. These four formulas are quite easy to understand for the students but from this concept, students can expect a lot of complex and indirect problems for the main examination. So, students must keep practising questions from this chapter every day. It is suggested that students should practice all the sums that are given in the NCERT textbook and students can also avail Selina publisher’s textbook and practice this topic with the help of the textbook.
How does the Selina Textbook help to achieve Better Results for the Class 10 ICSE Board Exams?
The Selina Concise textbook can be used for the preparation of the board exams. The questions given in this textbook are more than enough for this chapter’s preparation. This textbook follows all the guidelines set by the ICSE board and is the most reliable textbook for the students. The answers are given in a step-by-step manner to ensure students get the best quality of education. The explanations are precise and to the point. There are miscellaneous exercises too. Students can learn and practice with it. The textbook also contains chapter-wise questions. This textbook will be useful for Class 10 students who can make the most out of it and try to achieve better results.
FAQs on Concise Mathematics Class 10 ICSE Solutions for Chapter 22 - Heights and Distances
1. Where can I get the Selina Concise Mathematics solution for Class 10 ICSE Chapter 22 Heights and Distances?
The Selina Concise Mathematics solutions for Class 10 ICSE Chapters and distances are available on the website of Vedantu. The Vedantu website provides all the reading materials free of cost. Students can also avail of all these materials for free for the preparation. The textbook also provides all the possible questions along with the answers that are explained in detail. Since, there is a step-by-step explanation, it will be easy for the students to track their mistakes and practice better.
You can avail all the well-researched and good quality chapters, sample papers, syllabus on various topics from the website of Vedantu and its mobile application available on the play store.
2. Why is revision so important for ICSE Class 10 Mathematics Chapter 22 Selina Concise Solutions for Class 10 students?
Revision is the key thing in the preparation for the Class 10 board exam. Since students study a lot of formulas, theorems and concepts, it might get difficult to retain all the information in the longer run. So to get hold of everything they have studied previously, it is important to revise. Generally, the brain is accustomed to remember only the most recent concept, so it is important to keep revising all the previously read concepts in order to remember them for the board exams. Practice and revision are the key points to remember when preparing for the board exams.
3. How does the Vedantu website help the students to score higher marks in Chapter 22 Mathematics for Class 10 ICSE board?
Vedantu provides services like offering the study material of syllabus, important questions, mock tests, previous year question paper, and doubts clarification sessions. All these services are provided free of cost for the students. The syllabus is updated as per the guidelines of the ICSE board. The important questions and mock tests are set by our team and the subject experts. Doubts can be posted on the website wall or students can register for free online doubt clarification sessions.
4. How do you calculate height and distance?
To calculate the height and distance, there are formulas for it. It is an easy to understand formula. In simple words, the calculation of the height and distance is calculated by the calculation of the height of an object is achieved by the measurement of the distance from the object. This includes the angle of elevation at the top of the object while calculating the height. You can refer to the Seline concise textbook to practice more questions for the exams.
5. Why is it important to study important marked questions for Class 10 board exams when it approaches near?
The important questions are mandatory for students to solve and prepare before going to the exam especially, when they are in Class 10 because it gives them the confidence to face the exam. It makes them feel confident because they know that they have covered almost all the concepts and also practiced important questions. By doing so, students can review their performance themselves and understand where they lack, and can focus more on it. It is an important skill to revise the whole curriculum in a short span of time.





































