JEE Advanced 2025 Revision Notes for Chemistry Gaseous and Liquid States

Matter exists in three different states:

• Solids

• Liquids

• Gases

Properties of Gases:

1. No definite shape nor volume.

2. Volume of gas = volume of the container

3. Undergoes compression and expansion.

4. Intermolecular distance is very high.

5. Volume depends on its pressure and temperature.

6. Intermixes with each other to form a homogenous mixture.

7. Gravitational forces have the least influence on the velocities of gas molecules.

8. Gases can expand freely into the space available to them this property is known as diffusion of gases.

S.T.P or N.T.P Conditions

Measurable Properties of Gases:

At Absolute Zero 

• Molecular motion in the gas ceases.

• Pressure and volume of the gas becomes zero.

• Kinetic energy of the gas becomes zero.

Gas law:

The laws which relate the properties of gases like pressure, volume, mass, and temperature are called gas law.

Boyle’s law

At constant temperature, the volume of a given mass of gas is inversely proportional to its pressure $v\alpha \dfrac{1}{p} \to pv = k$.

Shapes: 

P vs V	Hyperbola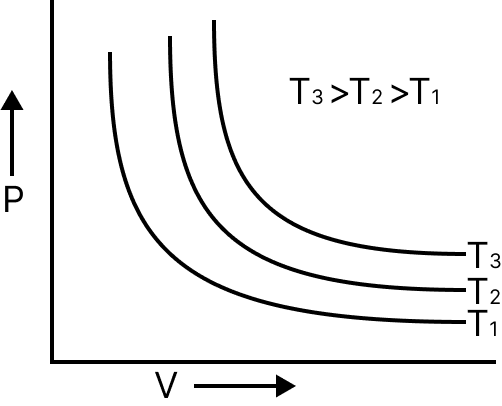
$p\alpha \dfrac{1}{v}$	$P = K.\dfrac{1}{V}$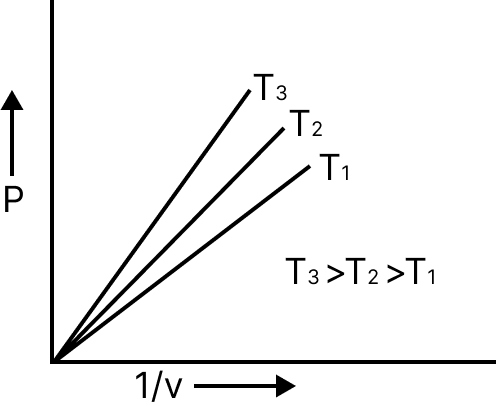
Pressure and PV	Straight line, parallel to the pressure axis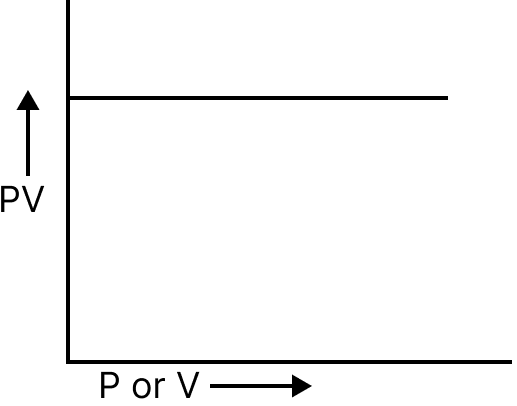

Relation between density and pressure of gas $d\alpha P$. Gases obey Boyle’s law at pressure and high temperature.

Charle’s Law:

At constant pressure, the volume of the given mass of a gas increase or decreases by $\dfrac{1}{{273.15}}$ times its volume at 0℃, for every 1℃ rise or fall in temperature

${V_t} = {V_0}(1 + \alpha t)$, α=volume coefficient=$\dfrac{1}{{273.15}}$

${V_t} = {V_0} + \dfrac{{{V_0}}}{{273.15}} \times {t^0}C$.

Avogadro’s Law:

Equal volume of all gases, measured under the same conditions of temperature and pressure contains equal number of molecules or moles.

$V\alpha n$ (P, T are constant) $\dfrac{V}{n} = K$

At a given temperature and pressure the density of gas is directly proportional to the molar mass of gas.

Ideal Gas:

A gas which obeys all the gas law under all the conditions of temperature and pressure is called ideal gas.

$PV = nRT$ is an ideal gas(or) perfect gas equation.

Graham’s Law of Diffusion:

The process of effusion is the diffusion of gas through a fine hole or narrow aperture.

Rate of Diffusion = $\dfrac{{\text{Volume of gas(V)}}}{{\text{Time(t)}}} = \dfrac{{\text{Distance travelled(l)}}}{{\text{Time(t)}}} = \dfrac{{\text{Number of moles of gas}}}{{\text{time}}}$

$\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{{V_1}}}{{{V_2}}} \times \dfrac{{{t_2}}}{{{t_1}}}$

Diffusion at Different Conditions:

Dalton’s Law of Partial Pressure 

The total pressure exerted by a mixture of non-reacting gases is equal to the sum of the partial pressures of component gases present in the mixture at the same temperature.

1. $P = {P_1} + {P_2} + {P_3} + ...... + {P_n}$

2. ${P_{\min }} = \left( {{n_1} + {n_2} + {n_3} + ...... + } \right)\dfrac{{RT}}{V}$
   
   

Partial Pressure:

Pressure exerted by a gas, when it alone occupies the total voile of the mixture at the same temperature is called partial pressure.

P.P of gas = total pressure × mole fraction of gas

Mole fraction of A is ${X_A} = \dfrac{{{n_A}}}{{{n_A} + {n_B}}}$

• The pressure exerted by the water vapour on its liquid surface when it is in dynamic equilibrium is called aqueous tension.

${P_{moist gas}} = {P_{dry gas}} + aqueous tension$

Aqueous tension is constant at a given temperature and increases with increase in temperature.

$P.Pgas = \dfrac{{V\% }}{{100}} \times totalpressure$

Relative humidity=

$\dfrac{{\text{partial pressure of}{H_2}\text{Oinair}}}{{\text{vapour pressure of}{H_2}O}}$

Kinetic Gas Equations:

$PV = \dfrac{1}{3}mn{C^2}$ is called Kinetic gas equation

$PV = \dfrac{1}{3}M{C^2}$

$p = \dfrac{1}{3}d{c^2}$

Where, m= mass of the molecules

M = Molar mass (m × n) 

C = RMS Velocity

All Gas Laws Can be Derived from the Kinetic Gas Equation:

Kinetic Energy of Gas:

• Kinetic energy of n moles of gas ${E_k} = \dfrac{3}{2}nRT$.

• The kinetic energy for one mole of gas ${E_K} = \dfrac{3}{2}RT$.

• The kinetic energy for one molecule of the gas ${E_K} = \dfrac{3}{2}KT(K = \dfrac{R}{N} = Boltzman cons)$.

• The average kinetic energy per molecule of any gas is the same as the same temperature.

• The values of Boltzmann constant are  

$K = 1.38 \times {10^{16}}erg{k^{ - 1}}molecul{e^{ - 1}}$

$K = 1.38 \times {10^{ - 23}}joule{k^{ - 1}}molecul{e^{ - 1}}$

• The relation between K.E, moles and temperature $\dfrac{{K.{E_1}}}{{K.{E_2}}} = \dfrac{{{n_2}}}{{{n_1}}} \times \dfrac{{{T_1}}}{{{T_2}}}$

Distribution of Molecular Velocities

RMS Velocity (Crms):

The square root of the mean of the square of the velocities of all the molecules present in the gas at any temperature is known as RMS velocity. 

$C = \sqrt {\dfrac{{C_1^2 + C_2^2 + C_3^2 + ...... + C_n^2}}{n}}$

$C = \sqrt {\dfrac{{3RT}}{M} = } \sqrt {\dfrac{{3PV}}{M} = } \sqrt {\dfrac{{3P}}{d}}$

$C = 1.58 \times {10^4} \times \sqrt {\dfrac{T}{M}cm.{{\sec }^{ - 1}}}$

• For a gas at different temperature $\dfrac{{{C_1}}}{{{C_2}}} = \sqrt {\dfrac{{{T_1}}}{{{T_2}}}}$.

• For two different gases having the same RMS velocity $\dfrac{{{T_1}}}{{{M_1}}} = \dfrac{{{T_2}}}{{{M_2}}}$.

• For two gases at the same temperature T $\dfrac{{{C_1}}}{{{C_2}}} = \sqrt {\dfrac{{{M_2}}}{{{M_1}}}}$.

• For two gases at different T $\dfrac{{{C_1}}}{{{C_2}}} = \sqrt {\dfrac{{{T_1}}}{{{T_2}}} \times \dfrac{{{M_2}}}{{{M_1}}}}$.

Average Velocity

The average of the velocity of all the molecules in the gas at any temperature.

$\bar C = \sqrt {\dfrac{{8RT}}{{\pi M}} = } \sqrt {\dfrac{{8PV}}{{\pi M}} = } \sqrt {\dfrac{{8P}}{{\pi d}}}$

$\bar C = 0.9213 \times RMS velocity$

Most Probable Velocity (Cp)

Velocity possessed by the maximum number of molecules present in the gas under given condition:

${C_P} = \sqrt {\dfrac{{2RT}}{M} = } \sqrt {\dfrac{{2PV}}{M} = } \sqrt {\dfrac{{2P}}{d}}$

Relation Between Molecular Velocities:

${C_P}:\bar C:C = \sqrt 2 :\sqrt {\dfrac{8}{\pi }: \sqrt 3 }$

$= 0.8166:0.9213:1$

(or) = 1:1.128:1.224

Collision Frequency and Mean Path:

= Average distance travelled by a gas molecule on unit time $\left(U_{a v}\right) /$ Number of collisions made by gas molecule in unit time $\left(N^{*}\right)$.

$\lambda  = \dfrac{1}{{\sqrt 2 \pi {\sigma ^2}{N^*}}} = \dfrac{{kT}}{{\sqrt 2 \pi {\sigma ^2}P}}$

Degree of Freedom:

Three for monoatomic gas: Five for diatomic gas

For a molecule having N atom, total 3N 

Translation: 3 for all types (at all temp)

Rotational: 2 for linear 3 for non linear

Each contributing $\dfrac{1}{2}KT$

Law of Equation of Energy:

• Translation Motion: ${\bar E_{trans}} = \dfrac{3}{2}kT$

• Rotational Motion: ${\bar E_{rot}} = \dfrac{3}{2}kT(non - linear)$

• Vibrational Motion: ${\bar E_{vib}} = \dfrac{1}{2}kT + \dfrac{1}{2}kT = 1kT(\text{per degree of freedom})$

Real Gases:

The gases which do not obey gas laws under all conditions of temperature and pressure are called real gases.

Compressibility Factor (Z):

The ratio of the actual molar volume of a gas to the molar volume of a perfect gas under the same condition.

$Z = \dfrac{{P.{V_m}}}{{RT}}$

Conditions of Z for Gases:

Boyle Temperature:

The temperature at which a real gas obeys ideal gas law over a wide range of pressure.

${T_b} = \dfrac{a}{{bR}}$

The Vander Waal’s Equation of State:

Volume Correction: $b = {N_A}[4\left( {\dfrac{4}{3}\pi {r^3}} \right)]$, NA = Avogadro number

Pressure Correction: Pressure correction $\alpha {\left( {\dfrac{n}{V}} \right)^2}$

$\left( {p + \dfrac{{a{n^2}}}{{{V^2}}}} \right)\left( {V - nb} \right) = nRT$ for ‘n’ moles.

If the radius of the molecule is given, then b can be calculated from $b = 96 \times {10^{23}} \times {r^3}$.

Condition of Liquefaction of Gases:

Joule-Thomson Effect: Cooling of gas by expansion from high pressure to low pressure 

Inversion Temperature: temperature below which if a gas is allowed to expand. It causes a cooling effect, above which on expansion the gas gets heated ${T_i} = \dfrac{{2a}}{{bR}}$.

Critical Constant in Terms of Vander Waals Constants a, b

${V_C} = 3b,{P_c} = \dfrac{a}{{27{b^2}}},{T_c} = \dfrac{{8a}}{{27Rb}}$

$z = \dfrac{{{P_c}{V_c}}}{{R{T_c}}} = \dfrac{3}{8}$

Boyle temperature and critical temperature in terms of Vander Waals constants:

${T_B} = \dfrac{a}{{Rb}},{T_c} = \dfrac{{8a}}{{27Rb}}$

Thus, ${T_B} > {T_C}$

${T_i},{T_b},{T_c}$ are related as ${T_i} > {T_b} > {T_c}$

Law of Corresponding States: $\left( {\pi  + \dfrac{3}{{{\phi ^2}}}} \right)\left( {3\phi  - 1} \right) = 8\theta$ ${T_i}$

Collision Frequency and Mean free path:

The collision rate i.e, the number of collisions taking place in unit time per unit volume is called collision frequency.

Z = Average number of collision made by molecule in unit time/length of the interval

RMS velocity(C) = 

$\dfrac{\lambda }{{\dfrac{1}{Z}}} = \lambda Z$

$\lambda  = \dfrac{1}{{\sqrt 2 \pi {r^2}n}}$, where n is the number of molecules per unit volume.

Viscosity: Strong intermolecular forces between the molecules of successive layer of liquid holding them together.

The regular gradation of velocity for layer in passing from one layer to the next layer is called “laminar flow”.

$F\alpha A,F\alpha \dfrac{{dv}}{{dx}}$

$\therefore F = \eta A.\dfrac{{dv}}{{dx}},\eta  = A.{e^{E/RT}}$

n - proportionality constant; it is the measure of viscosity.

The SI unit for n is $\mathrm{Nm}^{-2} \mathrm{~S}$ (or) Pascal.

C.G.S unit is “poise”

$1 \text { poise } =1 \mathrm{~g} \mathrm{~cm}^{-1} \cdot \mathrm{s}^{-1} = {10^{ - 1}}kg{m^{ - 1}}{s^{ - 1}}$.

Importance of JEE Advanced Physical Chemistry Gaseous and Liquid States

Physical Chemistry Gaseous and Liquid States is an important chapter for the JEE Advanced students. This chapter introduces students to gas laws, absolute temperature, and other fundamental concepts. These concepts and scientific principles will be used throughout the Chemistry syllabus for this competitive exam.

The introduction and derivation of Charles’ Law, Boyle’s Law, and the combined representation of both of them will teach students how gas behaves in the ideal conditions when the pressure and temperature of a system are changed. Delve deeper to understand the Kinetic Theory of Gases described in this chapter. Learn how the molecules of different gases behave in a mixture.

It will also explain how to draw the graphical representation of these laws to understand the effects of changing different parameters on gases and liquids. Gaseous state notes will aid you to describe and understand the ideal gas equation, Avogadro’s Number and hypothesis.

Using these notes you will be able to understand the scientific principles and solve questions related to this chapter. These principles will be used in all relevant phases where gases and liquids are involved. Thus, you can prepare a strong conceptual foundation by referring to these notes.  

Benefits of Gaseous and Liquid States Revision Notes

• The subject matter experts at Vedantu have elaborated all the gas laws and relevant equations mentioned in this chapter for your better understanding. Every term in these laws and equations will be explained methodically so that you can implement them to answer explanatory and calculative questions easily.

• Understand deeply the meaning and implications of states of matter. Imbibe the concepts of fluids, pressure, volume, and temperature without any difficulty by referring to Vedantu’s revision notes for JEE Advanced Physical Chemistry Gaseous and Liquid States.

• Prepare yourself for the JEE Advanced exam by solving the questions related to these concepts. Understand how to decode a graph by following the explanation given in the revision notes. Clarify doubts on your own and find out how to solve the problems related to gases and liquids.

Download Gaseous and Liquid States Revision Notes Free PDF

Get the free PDF version of the revision notes for this chapter and complete your study material. Learn how the molecules of gases behave in a closed system. Find how the different laws and their derived equations can be used for solving problems. Check how the experts have explained the laws and principles to fortify your conceptual knowledge for this chapter.

Important Related Links for JEE Main and JEE Advanced