Answer
102k+ views
Hint: When the body is at rest the energy of that body is always conserved. When the object is moving it is continuously undergoing an energy transformation. The work done in stretching a string is equal to the potential energy stored in the spring.
Complete step by step solution:
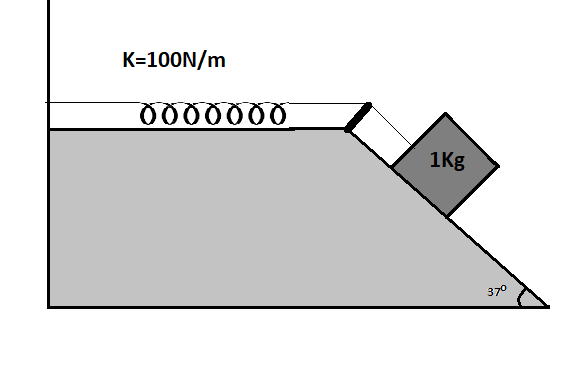
Here it is given that the surface is rough and spring is at rest and when the block is allowed to move then it moves to 10 cm before coming to rest. What it means is that after 10cm the frictional force due to friction will overcome the remaining force which was causing the object to move and the object stops.
To solve such problems we need to draw a free body diagram. It is a diagram that shows all the forces acting on the body and resolves them into the components. Refer to the figure below
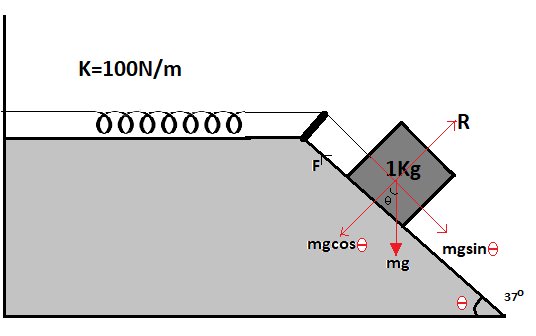
Here the weight of the body will act vertically downward ad when we resolve it there will be two-component of it $mg\cos \theta $ and $mg\sin \theta $ as shown in the figure
The reactionary force R will be acting vertically away from the block as the object is moving down the inclined plane the direction of the frictional force will be acting up the plain here friction force is shown by F and its direction is up the incline
Now according to newton's law, we know that a body moves only when there is a residual force on it
Now the body is moving down the plane and there are only two forces F and $mg\sin \theta $ which will be responsible for the residual force which is causing motion in the object as the. The object is moving down the force $mg\sin \theta $must be greater than frictional force (F)so that the object moved in that direction
Now resultant of these two forces will be given by
${F_r} = mg\sin \theta - F$
Now as we know the value frictional force is equal to the product of the coefficient of friction and reactionary force
$F = \mu R$
Now as we know that according to the law of conservation of energy if a body is at rest its energy is always conserved
So here when the object has moved by 10 cm
The energy equation for the situation can be written as
Work done by the block is equal to the potential energy in the spring
As we know work is done is the product of the force applied and distance
So here work done by the block will be a resultant force on the block multiplied by the distance it moved
$W = F \times D$
$W = \left( {mg\sin \theta - F} \right)x$
Where $x$is the distance moved by the object
And the potential energy stored in the spring is
\[PE = \dfrac{1}{2}k{x^2}\]
Where $k$is the spring constant and $x$ is the distance spring is stretched.
Equating both we get
$\Rightarrow \left( {mg\sin \theta - F} \right)x = \dfrac{1}{2}k{x^2}$
$\because F = \mu R$
Substituting it in the above equation we get
\[\Rightarrow \left( {mg\sin \theta - \mu R} \right)x = \dfrac{1}{2}k{x^2}\]
Now from the free body diagram, we can see that since the object is ion equilibrium so,
$\Rightarrow R = mg\cos \theta $
On substitution we get
\[\Rightarrow \left( {mg\sin \theta - \mu mg\cos \theta } \right)x = \dfrac{1}{2}k{x^2}\]
$ \Rightarrow mg\left( {\sin \theta - \mu \cos \theta } \right) = \dfrac{1}{2}k{x^2}$
Since $\theta = 37^\circ $
$\Rightarrow x = 10cm = 0.1m$
$\Rightarrow m = 1kg$
$\Rightarrow k = 100N/m$
$ \Rightarrow 1 \times 9.81\left( {\sin 37^\circ - \mu \cos 37^\circ } \right) = \dfrac{1}{2} \times 100 \times {\left( {0.1} \right)^2}$
\[ \Rightarrow \mu = \dfrac{{0.092}}{{0.799}} = 0.115\]
The value of the coefficient of friction $\mu $ will be 0.115.
Note: Frictional force always acts opposite to the direction of motion. The value of frictional force is always the product of reaction force and coefficient of friction u. When a body is at rest position all the forces cancel out each other and the is no resultant force on the object.
Complete step by step solution:
Here it is given that the surface is rough and spring is at rest and when the block is allowed to move then it moves to 10 cm before coming to rest. What it means is that after 10cm the frictional force due to friction will overcome the remaining force which was causing the object to move and the object stops.
To solve such problems we need to draw a free body diagram. It is a diagram that shows all the forces acting on the body and resolves them into the components. Refer to the figure below

Here the weight of the body will act vertically downward ad when we resolve it there will be two-component of it $mg\cos \theta $ and $mg\sin \theta $ as shown in the figure
The reactionary force R will be acting vertically away from the block as the object is moving down the inclined plane the direction of the frictional force will be acting up the plain here friction force is shown by F and its direction is up the incline
Now according to newton's law, we know that a body moves only when there is a residual force on it
Now the body is moving down the plane and there are only two forces F and $mg\sin \theta $ which will be responsible for the residual force which is causing motion in the object as the. The object is moving down the force $mg\sin \theta $must be greater than frictional force (F)so that the object moved in that direction
Now resultant of these two forces will be given by
${F_r} = mg\sin \theta - F$
Now as we know the value frictional force is equal to the product of the coefficient of friction and reactionary force
$F = \mu R$
Now as we know that according to the law of conservation of energy if a body is at rest its energy is always conserved
So here when the object has moved by 10 cm
The energy equation for the situation can be written as
Work done by the block is equal to the potential energy in the spring
As we know work is done is the product of the force applied and distance
So here work done by the block will be a resultant force on the block multiplied by the distance it moved
$W = F \times D$
$W = \left( {mg\sin \theta - F} \right)x$
Where $x$is the distance moved by the object
And the potential energy stored in the spring is
\[PE = \dfrac{1}{2}k{x^2}\]
Where $k$is the spring constant and $x$ is the distance spring is stretched.
Equating both we get
$\Rightarrow \left( {mg\sin \theta - F} \right)x = \dfrac{1}{2}k{x^2}$
$\because F = \mu R$
Substituting it in the above equation we get
\[\Rightarrow \left( {mg\sin \theta - \mu R} \right)x = \dfrac{1}{2}k{x^2}\]
Now from the free body diagram, we can see that since the object is ion equilibrium so,
$\Rightarrow R = mg\cos \theta $
On substitution we get
\[\Rightarrow \left( {mg\sin \theta - \mu mg\cos \theta } \right)x = \dfrac{1}{2}k{x^2}\]
$ \Rightarrow mg\left( {\sin \theta - \mu \cos \theta } \right) = \dfrac{1}{2}k{x^2}$
Since $\theta = 37^\circ $
$\Rightarrow x = 10cm = 0.1m$
$\Rightarrow m = 1kg$
$\Rightarrow k = 100N/m$
$ \Rightarrow 1 \times 9.81\left( {\sin 37^\circ - \mu \cos 37^\circ } \right) = \dfrac{1}{2} \times 100 \times {\left( {0.1} \right)^2}$
\[ \Rightarrow \mu = \dfrac{{0.092}}{{0.799}} = 0.115\]
The value of the coefficient of friction $\mu $ will be 0.115.
Note: Frictional force always acts opposite to the direction of motion. The value of frictional force is always the product of reaction force and coefficient of friction u. When a body is at rest position all the forces cancel out each other and the is no resultant force on the object.
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Name the scale on which the destructive energy of an class 11 physics JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main