Question

A block $A$ slides over another block $B$ which is placed over a smooth inclined plane. The coefficient of friction between the two blocks $A$ and $B$ is $\mu $. Mass of block $B$ is two times the mass of block $A.$ The acceleration of the centre of mass of two blocks is:

A) $g\sin \theta $
B) $\dfrac{{g\sin \theta - \mu g\cos \theta }}{3}$
C) $\dfrac{{g\sin \theta }}{3}$
D) $\dfrac{{2g\sin \theta - \mu g\cos \theta }}{3}$

Answer 1

Hint: In order to find the solution of the given question first of all we need to find the force exerting on the centre of mass of the two bodies. Then we need to find the total acceleration of the centre of mass of the two blocks. After that we can finally conclude with the solution of the given question.

Complete step by step solution:
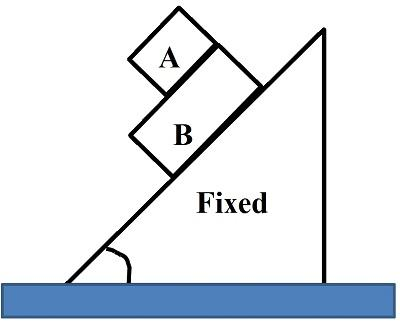
First of all let us find the total force acting on the block A.
The total force acting on the block $A$ will be, ${F_A} = mg\sin \theta - f$
Similarly, the total force acting on the block $B$will be,${F_B} = 2mg\sin \theta + f$
Now let us find the acceleration in block $A.$
We know that $F = ma$
$ \Rightarrow a = \dfrac{F}{m}$
Now, using this relation, we can find the acceleration in block$A.$It can be written as,
$\Rightarrow {a_A} = \dfrac{{{F_A}}}{{{m_A}}}$
Similarly, we can find the acceleration in block$B$and it can be written as,
$\Rightarrow {a_B} = \dfrac{{{F_B}}}{{{m_B}}}$
Now, let us find the acceleration of the centre of mass of the blocks $A$and$B$.
This can be written as,
$\Rightarrow {a_{com}} = \dfrac{{{m_A}\dfrac{{{F_A}}}{{{m_A}}} + {m_B} + \dfrac{{{F_B}}}{{{m_B}}}}}{{{m_A} + {m_B}}}$
$ \Rightarrow {a_{com}} = \dfrac{{{F_A} + {F_B}}}{{{m_A} + {m_B}}}$
Putting the values of force and mass of the two blocks in above equation we get,
$\Rightarrow {a_{com}} = \dfrac{{mg\sin \theta - f + 2mg\sin \theta + f}}{{m + 2m}}$
$ \Rightarrow {a_{com}} = \dfrac{{3mg\sin \theta }}{{3m}}$
$\therefore {a_{com}} = g\sin \theta $
Therefore, the required value of acceleration of the centre of mass is $g\sin \theta .$

Hence, option (A), i.e. $g\sin \theta $ is the correct choice of the given question.

Note: Acceleration of centre of mass is defined as the product of the total external force acting on the system and their total masses. The centre of mass is a point at which the whole mass of the system is concentrated. We should also know this fact that the centre of mass is just an imaginary point where we consider that the entire mass of the body is supposed to be concentrated.