Question

A broad beam of light of wavelength 683nm is sent directly downward through the top plate of a pair of glass plates. The plates are 120mm long, touch at the left end, and are separated by $48.0\mu m$ at the right end. The air between the plates acts as a thin film. How many bright fringes will be seen by an observer looking down through the top plate?

Answer 1

Hint Bright or dark fringe pattern is a result of interference or diffraction. Interference occurs when two waves superimpose onto each other. Here, we observe the superimposition of two reflected waves. You have to recall that when a wave reflects normally from the surface of a denser medium back into the rarer medium, a phase difference of $\pi $ is introduced.

Complete Step by step solution

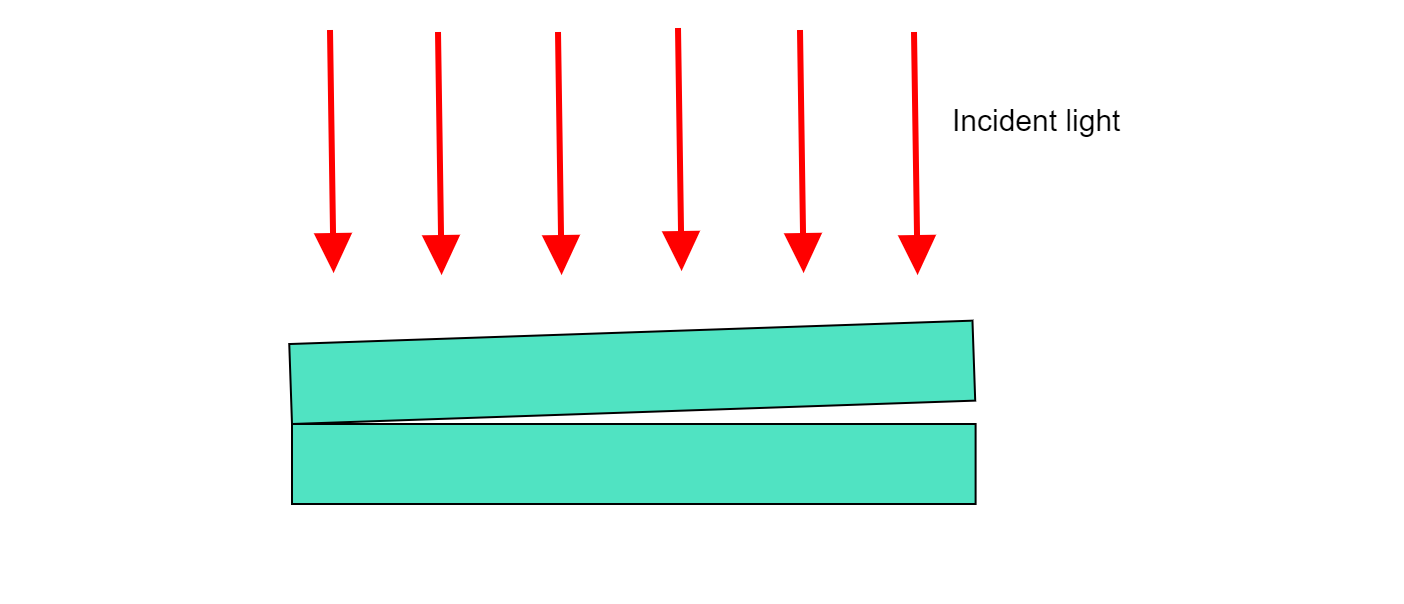
In this problem, the interference of the two waves is taking place. One is reflected from the plate-air interface (top of the air thin film) and the other is reflected from the air-plate interface (bottom of the air thin film).
We know that, any wave that is reflected normally from the surface of a rarer medium back into the denser medium undergoes no phase change. However, the same cannot be said for a wave reflected normally from the surface of the denser medium back into the rarer medium. In such cases, a phase difference of $\pi $ is introduced.
In the case of thin- film interference, the condition for constructive interference is given as,
 $2L = \left( {n + \dfrac{1}{2}} \right)\lambda $ $ - - - - (1)$
where,
 $L$ is the thickness of the thin film,
 $\lambda $ is the wavelength of the light.
For this problem, we consider the right most part of this system, where the thickness of the thin film is $48.0\mu m$ .
Thus, $L = 48\mu m$ .
 $ \Rightarrow L = 48 \times {10^ - }^6m$
Given, $\lambda = 683nm$ .
 $ \Rightarrow \lambda = 683 \times {10^ - }^9m$
Using these numerical values in equation (1), we get
 $2 \times 48 \times {10^ - }^6 = \left( {n + \dfrac{1}{2}} \right)683 \times {10^ - }^9$
 $ \Rightarrow \left( {n + \dfrac{1}{2}} \right) = \dfrac{{2 \times 48 \times {{10}^ - }^6}}{{683 \times {{10}^ - }^9}}$
Solving this, we get
 $\left( {n + \dfrac{1}{2}} \right) \simeq 140.5$
 $ \Rightarrow n = 140$ .
So, $140$ bright fringes will be seen by an observer looking down through the top plate.

Note The condition for bright or dark fringes should be correct to approach such problems. Often units of wavelength, thickness, etc. are not SI units. Converting them to the SI unit will help you to avoid any mistakes.