Question

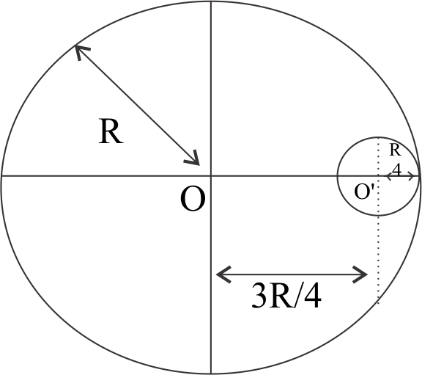
A circular hole of radius $\dfrac{R}{4}$ is made in a thin uniform disc having mass M and radius R, as shown in figure. The moment of inertia of the remaining portion of the disc about an axis passing through the point O and perpendicular the plane of the disc is:


(A) $\dfrac{{197M{R^2}}}{{256}}$
(B) $\dfrac{{19M{R^2}}}{{512}}$
(C) $\dfrac{{237M{R^2}}}{{512}}$
(D) $\dfrac{{219M{R^2}}}{{256}}$

Answer 1

Hint We can understand the question by looking into the given diagram. In a thin uniform disc a circular hole of radius $\dfrac{R}{4}$ is made. To have to find the moment of inertia of the remaining portion of the disc. We have to subtract the inertia of the circular hole made from the inertia of the disc.

Complete step by step answer
Moment of inertia is also known as angular mass or rotational inertia. It is the torque required for an angular acceleration about an axis of rotation. It is represented by I. The moment of inertia is specified with a chosen axis of rotation. It depends on the distribution of mass around the axis of rotation i.e. the moment of inertia varies depending on the axis of rotation. Basically, moment of inertia is used to calculate the angular momentum.
In other words it is the product of mass of particle in the axis of rotation and the square of distance from the axis of rotation. Its unit is $Kg\,{m^2}$
Which is,
${\text{I}} = m \times {r^2}$
Where,
$I$ is the moment of inertia.
$m$ is the sum of product of all the mass.
$r$ is the distance from the axis of rotation.
The moment of inertia experienced by a circular body is given by
${\text{I}} = \dfrac{1}{2}m{r^2}$
$I$ is the moment of inertia.
$m$ is the sum of product of all the mass.
$r$ is the distance from the axis of rotation.
Given that,
In a thin uniform disc a circular hole of radius $\dfrac{R}{4}$ is made
The mass of the disc is M
The radius of the disc is R
The radius of the circular hole made in the disc is $\dfrac{R}{4}$
Since a hole is made a circular section of radius $\dfrac{R}{4}$ is removed and that hole is at a separation of $\dfrac{{3R}}{4}$ from the centre (From the diagram)
Mass of the section removed is given by the surface mass density relation
Surface mass density of circular disc is given by the formula
$ \Rightarrow \sigma = \dfrac{m}{A}{\text{ }} \to {\text{1}}$
$ \Rightarrow m = \sigma A{\text{ }} \to {\text{2}}$
Where,
$\sigma $ is the surface mass density
A is the area
m is the mass
We know that, area of a circle is $A = \pi {r^2}$
The equation 2 becomes
$ \Rightarrow m = \sigma A{\text{ }} \to {\text{2}}$
$ \Rightarrow m = \dfrac{m}{{{A_d}}}{A_h}$
${A_d}$ is the area of the disc
${A_h}$ is the area of the circular hole
$ \Rightarrow m = \dfrac{M}{{\pi {R^2}}} \times \pi {\left( {\dfrac{R}{4}} \right)^2}$
$ \Rightarrow m = \dfrac{M}{{16}}$
Mass of the section removed, $m = \dfrac{M}{{16}}$
The moment of inertia of the axis passing through centre of the axis
$ \Rightarrow {\text{I}} = \dfrac{1}{2}m{r^2}$
$ \Rightarrow {{\text{I}}_c} = \dfrac{1}{2}\dfrac{M}{{16}}{\left( {\dfrac{R}{4}} \right)^2}$
$ \Rightarrow {{\text{I}}_c} = \dfrac{1}{2}\dfrac{M}{{16}}\left( {\dfrac{{{R^2}}}{{16}}} \right)$
$ \Rightarrow {{\text{I}}_c} = \dfrac{{M{R^2}}}{{512}}$
By parallel axis theorem
$ \Rightarrow I = {I_c} + m{d^2}$
I is the moment of inertia
${I_c}$ is the moment of inertia through the centre
m is the mass of the body
d is the distance between two axis
\[ \Rightarrow I = \dfrac{{M{R^2}}}{{512}} + M{\left( {\dfrac{{3R}}{4}} \right)^2}\]
\[ \Rightarrow I = \dfrac{{M{R^2}}}{{512}} + M\dfrac{{9{R^2}}}{{16}}\]
\[ \Rightarrow I = \dfrac{{M{R^2}}}{{512}} + M\dfrac{{9{R^2}}}{{16}}\]
Taking LCM we get
\[ \Rightarrow I = \dfrac{{19}}{{512}}M{R^2}\]
The moment of inertia of the remaining portion of the disc is derived by subtracting the moment of inertia of the circular hole (mass removed) from the moment of inertia of the disc
$ \Rightarrow {I_R} = {I_d} - I$
$ \Rightarrow {I_R} = \dfrac{1}{2}M{R^2} - \dfrac{{19}}{{512}}M{R^2}$
Taking LCM we get
$ \Rightarrow {I_R} = \dfrac{{237}}{{512}}M{R^2}$
The moment of inertia of the remaining portion of the disc is \[\dfrac{{237}}{{512}}M{R^2}\]

Hence the correct answer is option (C) \[\dfrac{{237}}{{512}}M{R^2}\]

Note The moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of the body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes.
$ \Rightarrow I = {I_c} + m{d^2}$