Question

A conducting rod makes contact with a partial circuit and completes the circuit as shown. The circuit area is perpendicular to a magnetic field $B = 0.25T$. How large force is needed if the total resistance of the circuit is to move the rod as indicated with a constant speed of $4m/s$ apart from the force $F = \dfrac{1}{{80}}N$ already acting in the direction shown?

Answer 1

Hint: As the rectangular rod moves, there is a change in the area. Due to this changing area, EMF is induced, as the changing area results in a change in a magnetic field. From the expression of induced EMF, we can obtain the value of induced current, and using it, and we can get the value of force attaining.

Complete step by step solution:
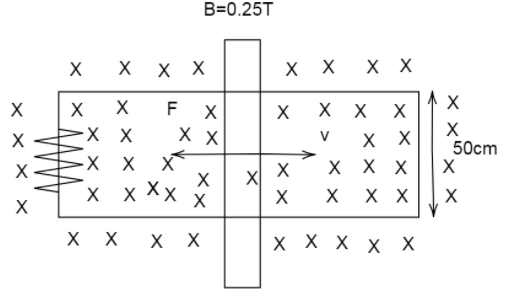
From Faraday's law of electromagnetic induction, we know that change in flux linkages results in an induced EMF in the coil. Now, it is given that the rod is placed in a uniform magnetic field. When the rod moves, there occurs a change in the area, resulting in a difference in the magnetic field. Thus emf is induced in this case.
Again, by Faradays’ law of electromagnetic induction, we know:
$e = Blv$
Where:
$e$ is Induced EMF
$B$ is Magnetic field
$l$ is Length
$v$ is Velocity
Thus, we obtain:
$\Rightarrow e = 0.25 \times 50 \times 4$
Hence, we get:
$\Rightarrow e = 0.5V$
It is given that the resistance of the loop,$R = 5\Omega$, therefore, we can find the induced current as:
$I = \dfrac{e}{R}$
Putting the values, we get:
$\Rightarrow I = \dfrac{{0.5}}{5} = 0.1A$
Now, the force experienced by the rod is given by:
$\Rightarrow F = BIl\sin {90^o}$
Thus, on putting the values, we get:
$\Rightarrow F = 0.25 \times 0.1 \times 50 \times {10^{ - 2}} \times 1$
On solving the equation, we get:
$\Rightarrow F = 0.0125N$
Therefore, the net force experience, by the rod is:
$\Rightarrow {F_{net}} = 0.0125N + \dfrac{1}{{80}}N$
Hence, we get:
$\Rightarrow {F_{net}} = 0.025N$
This is the required solution.

Note: The induced EMF will only be induced if the area associated with the magnetic field changes. However, if the loop is mo0ved in such a manner that the area remains in the magnetic field, then no EMF; as a result, no current will be induced. Hence, there would also be no force acting.