Question

A jar of height h is filled with the transparent liquid of refractive index $\mu $. At the center of the jar on the bottom surface is a dot. Find the minimum diameter of the disc such that when it is placed on the top surface symmetrically about the center, the dot is invisible.

Answer 1

Hint Using the trigonometry find the value for $\sin {i_c}$ and using $\sin {i_c}$ find the value for $\tan {i_c}$. Then, use the trigonometry for finding another expression for $\tan {i_c}$. Using both the expressions of $\tan {i_c}$ find the expression for the minimum diameter of the disc.

Key Concept


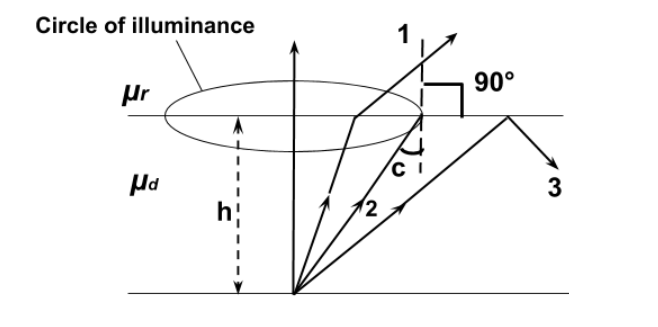
In the above figure, we can see that ray 1 is striking the surface having angle less than the critical angle which is denoted by $c$ and gets refracted in the rarer medium. The second ray strikes the surface at critical angle and grazes the interface and the third ray strikes the surface and makes the angle greater than critical angle and gets internally reflected. There is also a circle of illuminance which is the locus of points where ray strikes at a critical angle. The light rays which strike inside the circle of illuminance get refracted in the rarer medium. Imagine an observer in the rarer medium then, he/she will see the light coming only from the circle of illuminance. If a circle opaque plate covers the circle of illuminance then, no light will get refracted in the rarer medium and then the object cannot be seen from the rarer medium. In the figure, 0 is a small dot in the bottom of the jar. The ray from the dot emerges out of the circular patch of water surface of diameter AB till the angle of incidence for the rays OA and 013 exceeds the critical angle.

Complete Step by Step Solution
To find the minimum diameter of the disc we have to construct the figure –

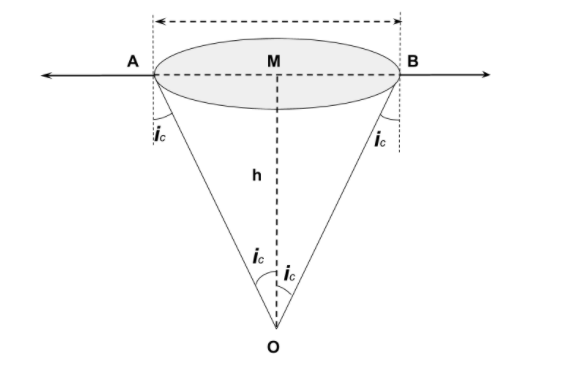
Let $d$ be the diameter of the disc. The spot shall be invisible if the incident rays from the dot at O to the surface at $\dfrac{d}{2}$ are at the critical angle.
From the figure, we can say that –
$\sin {i_c} = \dfrac{1}{\mu }$
In terms of tan, it can be expressed as –
$ \Rightarrow \tan {i_c} = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }} \cdots \left( 1 \right)$
Now, $\dfrac{{\dfrac{d}{2}}}{h} = \tan {i_c} \cdots \left( 2 \right)$
From equation (1) and (2), we get –
$
  \dfrac{1}{{\sqrt {{\mu ^2} - 1} }} = \dfrac{{\dfrac{d}{2}}}{h} \\
   \Rightarrow d = \dfrac{{2h}}{{\sqrt {{\mu ^2} - 1} }} \\
 $

Hence, this is the required expression of $d$.

Note Use the trigonometry carefully during finding of the expression for $\sin {i_c}$ and $\tan {i_c}$. As $\sin \theta $ can be found by dividing the perpendicular from the hypotenuse and for finding the $\tan \theta $ we have to divide the perpendicular from the base in the given triangle.