Question

A ray of light is coming along the line $y=b$ from the positive direction of x-axis and strikes a concave mirror whose intersection with the \[xy\] -plane is a parabola ${{y}^{2}}=4ax$. Find the equation of the reflected ray and show that it passes through the focus of the parabola. Both a and b are positive.

Answer 1

Hint: As the reflected ray passes through the focus and we know the coordinates of the focus. So first we will find the intersection of a ray of light and a concave mirror and then use the equation of line formula to find the required equation.

Complete step-by-step answer:
In a concave mirror if the ray of light is parallel to the axis of the mirror, then the reflected ray will pass through the focus of the concave mirror.
As per the information given, we can draw the diagram as follows.






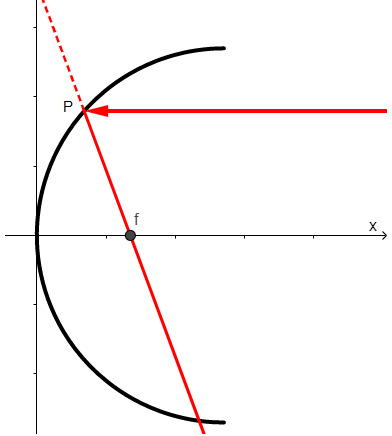
Let the ray of light meet the concave mirror at point P. Then Pf is the reflected ray where f is the focus of the concave mirror.
The equation of parabola or the equation of the concave mirror is,
${{y}^{2}}=4ax$
So, the coordinate of the point f will be $\left( a,0 \right)$.
As it is given that ray of light with equation $y=b$ strikes the concave mirror, so substituting the value of ‘y’ we get,
${{b}^{2}}=4ax$
$x=\dfrac{{{b}^{2}}}{4a}$
So, the coordinates of the point P is $\left( \dfrac{{{b}^{2}}}{4a},b \right)$ .
Now the slope of the line passing through two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is given by,
$m=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}$
So, the slope of the line passing through point \[f\left( a,0 \right)\] and \[P\left( \dfrac{{{b}^{2}}}{4a},b \right)\] is,
$m=\dfrac{b-0}{\dfrac{{{b}^{2}}}{4a}-a}$
$\Rightarrow m=\dfrac{b}{\dfrac{{{b}^{2}}-4{{a}^{2}}}{4a}}$
$\Rightarrow m=\dfrac{4ab}{{{b}^{2}}-4{{a}^{2}}}$
Now we know the line of equation passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$is,
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
where ‘m’ is the slope of the line.
So, the equation of line passing through the point \[f\left( a,0 \right)\]with slope, $m=\dfrac{4ab}{{{b}^{2}}-4{{a}^{2}}}$, is,
$y-0=\left( \dfrac{4ab}{{{b}^{2}}-4{{a}^{2}}} \right)\left( x-a \right)$
$\Rightarrow \left( {{b}^{2}}-4{{a}^{2}} \right)y=4ab\left( x-a \right)$
$\Rightarrow 4abx-4{{a}^{2}}b-\left( {{b}^{2}}-4{{a}^{2}} \right)y=0$
$\Rightarrow 4abx-\left( {{b}^{2}}-4{{a}^{2}} \right)y-4{{a}^{2}}b=0$
Now as the reflected ray is passing through the focus, i.e., f, so the equation of reflected ray is,
$4abx-\left( {{b}^{2}}-4{{a}^{2}} \right)y-4{{a}^{2}}b=0$

Note: In this instead using the slope form of the equation of line we can use the point form of equation of line formula as well. In both cases you will get the same answer.