Question

A simple magnifying lens is used in such a way that an image is formed at 25 cm away from the eye. In order to have 10 times magnification, the focal length of the lens should be:
A) 5cm
B) 2cm
C) 27 mm
D) 0.1mm

Answer 1

Hint: Before we solve the problem, we need to understand the type of lens used for magnification. The lens used for magnification is a convex lens only, since a concave lens produces only, diminished images. The position at which the convex lens produces the right magnification used in the magnifying lens, should be determined by the lens formula as given below –
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
where u = distance of object from pole, v = distance of image from pole and f = focal length of the lens.

Complete step by step answer:
A simple hand-held magnifying lens used to read small prints and study intricate details that are not visible to naked eye, is made of biconvex lens of positive focal length.
The biconvex lens (or simply, convex lens) produces a highly magnified and erect image if the object is placed between the pole and the focus. This is because the convex lens produces an highly enlarged virtual image behind the convex lens, which is easily viewable by the human eye. The ray diagram of this case of image formation is given as shown:

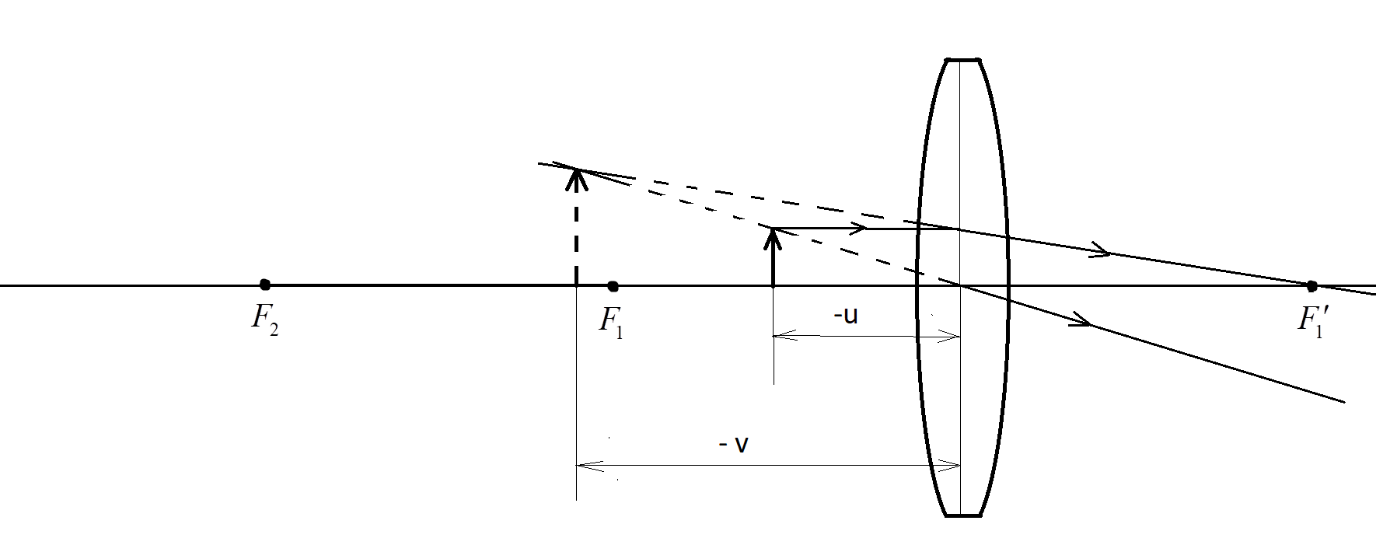
The object is placed at a distance $ - u$ and the image is formed at $v = - 25cm$.
The magnification due to lens is given by –
$m = \dfrac{v}{u}$
Given that the achieved magnification is equal to 10, we have –
$\Rightarrow 10 = \dfrac{v}{u}$
Substituting the values of u and v,
$\Rightarrow 10 = \dfrac{{\left( { - 25} \right)}}{u}$
$ \Rightarrow u = \dfrac{{ - 25}}{{10}} = - 2.5cm$
With the value of u and v, the focal length can be calculated by the formula –
$\Rightarrow \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{{\left( { - 25} \right)}} - \dfrac{1}{{\left( { - 2.5} \right)}} = \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{{2.5}} - \dfrac{1}{{25}} = \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{f} = \dfrac{{10 - 1}}{{25}}$
$ \Rightarrow f = \dfrac{{25}}{9} = 2.778cm = 27.78mm \simeq 27mm$
The focal length of the lens is equal to 27mm.

Hence, the correct option is Option C.

Note: The students can cross-check that they are in the correct path of solving the question if they obtain a positive value of focal length for convex mirror. If by some calculation, a negative value of the focal length is obtained, the students can be sure that the answer is surely wrong and should revisit the steps for calculation errors. This can help increase their accuracy.