Question

Find the total kinetic energy of ring by analyzing the figures shown

A) $\dfrac{3}{2}M\omega _0^2\left( {R - r} \right)$
B) $\dfrac{1}{2}M\omega _0^2\left( {R - r} \right)$
C) $M\omega _0^2{\left( {R - r} \right)^2}$
D) $M\omega _0^2{R^2}$

Answer 1

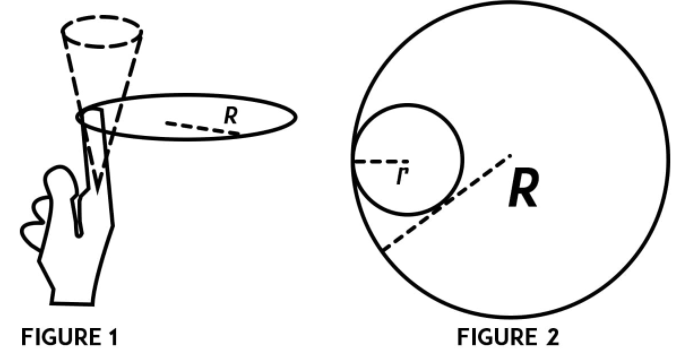
Hint: From the figure 2 given in the question we can see that the centre of mass of the ring moves in a circle of radius $R - r$.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
Where, $M$ is the mass of the ring and $v$ is the linear velocity
let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Therefore, \[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$

Complete step by step solution:
Let the mass of the ring be $M$ and its radius be $R$and $v$ be the linear velocity and let ${\omega _0}$ be the angular velocity of the centre of mass of the ring.
From the figure 2 given in the question we can see that the centre of mass of the ring moves in a circle of radius $R - r$.
The kinetic energy due to translation is given by the equation
\[{K_T} = \dfrac{1}{2}M{v^2}\]
We know that
$\omega = \dfrac{v}{r}$
That is, $v = \omega r$.
Now let us substitute all these values in the equation for translational kinetic energy.
\[{K_T} = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2}\]
The kinetic energy due to rotation is given by the equation
${K_R} = \dfrac{1}{2}I\omega _0^2$
Where, the moment of inertia of the ring $I = M{R^2}$.
Therefore,
${K_R} = \dfrac{1}{2}M{R^2}\omega _0^2$
Total kinetic energy is the sum of both kinetic energy due to translation and rotation.
$K = {K_T} + {K_R}$
Substitute the values of kinetic energy due to translation and rotation. Then, we get
$K = \dfrac{1}{2}M\omega _0^2{\left( {R - r} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2}{\left( {1 - \dfrac{r}{R}} \right)^2} + \dfrac{1}{2}M{R^2}\omega _0^2$
Since, $r < < R$
We can consider the term $\dfrac{r}{R} = 0$
$ \Rightarrow K = \dfrac{1}{2}M\omega _0^2{R^2} + \dfrac{1}{2}M{R^2}\omega _0^2 = M{R^2}\omega _0^2$

So, the correct answer is option (D).

Note: While substituting for the radius in the equation for kinetic energy due to translation, don't substitute the radius of the ring $R$. We need to consider the circle in which centre of mass moves. From the figure we can see that the radius of this circle will be $R - r$. Similarly, the angular velocity ${\omega _0}$ that we considered is the angular velocity of the centre of mass.