Question

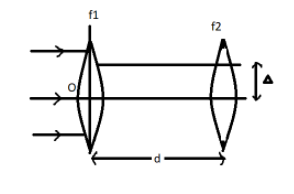
Find the $y$ coordinate of the focal of this lens system.

A) $\dfrac{{({f_1} + d)\Delta }}{{({f_1} + {f_2} - d)}}$
B) $\dfrac{{2({f_1} + d)\Delta }}{{({f_1} + {f_2} + d)}}$
C) $\dfrac{{2({f_1} - d)\Delta }}{{({f_1} + {f_2} + d)}}$
D) $\dfrac{{({f_1} - d)\Delta }}{{({f_1} + {f_2} - d)}}$

Answer 1

Hint: A lens is a Transmissive optical instrument that focuses or distributes a beam of light by refraction. A single piece of transparent material consists of a simple lens whereas a compound lens consists of multiple simple lenses (elements), typically arranged around a common axis. Objectives consist of glass or plastic materials and are soiled and polished or designed to a desired form. The lens, unlike a prism, can transform light into a picture and refract light. Often called lenses, such as microwaves, electron lenses, acoustic lenses or explosive lenses, are instruments that concentrate or scatter waves and radiation other than visible light.

Complete step by step solution:
The picture will form at the centre of the second lens after the refraction of parallel rays from the first lens. The first picture is created from the first lens at a distance of ${f_1}$ .
This picture is an object for second-lens refraction, for positioning the object
$u = {f_1} - d$
$u$ is the distance of object from first mirror
$d$ is the distance between two lens

Therefore,
$\dfrac{1}{v} - \dfrac{1}{{{f_1} - d}} = \dfrac{1}{{{f_2}}}$
$ \Rightarrow v = \dfrac {{({f_1} - d) {f_2}}} {{{f_1} + {f_2} - d}} $
The magnification can be written as,
$\dfrac {v} {u} = \dfrac{{{f_2}}}{{{f_1} + {f_2} - d}} $
The picture was created on the $x$ -axis after the refraction from the first lens, but the second lens is focused on the $x$ - axis at a distance of $\Delta $.
$m = \dfrac{y} {{- \Delta}}$
Hence,
$y = \dfrac {{- \Delta {f_2}}} {{{f_1} + {f_2} - d}} $
$y$ Coordinate with respect to the centre of first lens,
$\Delta + y = \Delta + \dfrac {{- \Delta {f_2}}} {{{f_1} + {f_2} - d}} $
$ \Rightarrow \dfrac {{({f_1} - d)\Delta}} {{{f_1} + {f_2} - d}} $

Hence correct option is (D).

Note: The curvatures in the two optical surfaces are labelled for the lenses. If the two sides are convex, a lens is biconvex (or double convex or just convex). The lens is equiconvex because all surfaces have the same curvature radius. Biconcave (or concave) is a lens with two concave surfaces. The lens is Plano-convex or Plano-concave while one of the surfaces is smooth, depending on the curvature in the other. Convex-concave or meniscus is a lens with one convex and one concave side. This is the most widely used type of lens in correction lenses.