Question

In the diagram shown, no friction at any contact surface. Initially the spring has no deformation, what will be the maximum deformation in the spring considering all the strings to be sufficiently large consider the spring constant to be K.

A) \[8F/3K\]
B) \[9F/3K\]
C) \[105F/3K\]
D) \[98F/3K\]

Answer 1

Hint: Using the theory of the system reaching a state of rest at maximum separation condition on the work done in the center of mass frame, we will deduce a formula with displacement. Then using the relation of center of mass of the two bodies in a system, we find out the displacement of the body $1$. Upon substitution of the determined data, we will find the value of maximum displacement.

Formulae used:
Work done in the center of mass frame in terms of weight of the bodies: \[{W_{spring}} + {W_F} + {W_{2F}} = 0\].
Where \[{W_{spring}},{W_F},{W_{2F}}\] are the work done of the spring, $2M$ block and $M$ block and is expressed in Joules $(J)$.
Work done in the center of mass frame in terms of kinetic energy, displacement and force of the bodies: \[ - \dfrac{1}{2}k{x^2}_{max} + {F_{x1}} + 2{F_{x2}} = 0\]
Where \[k\] is the spring constant, ${x_1},{x_2}$ are the displacements of the $2M$ block and $M$ block and is expressed in meter $(m)$ and $F$ is the force acting on the system and is expressed in Newton $(N)$.
Relation of center of mass of the two bodies in a system: \[{M_{x1}} = 2{M_{x2}}\]
Where \[{M_{x1}},{M_{x2}}\] are the masses of the $2M$ and $M$ block and are expressed in kilograms $(kg)$.

Complete step by step solution:


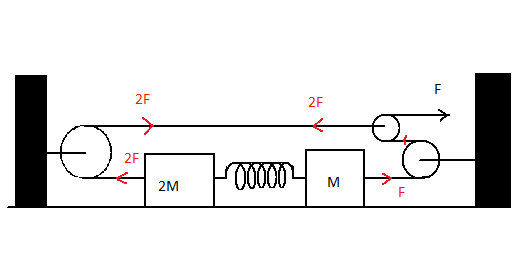
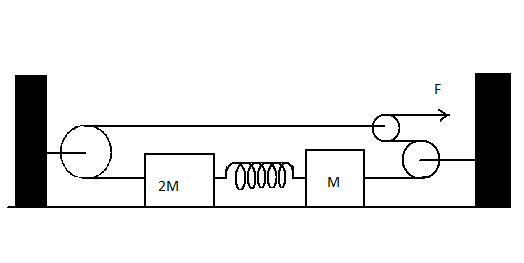
In the given system, the force acting on the block of mass $2M$ will have a force of $2F$ acting on it while the block $M$ will have force $F$ acting on it. On consideration of conditions in a state of maximum separation of the two blocks, the entire system comes to rest for a particular instant of time.

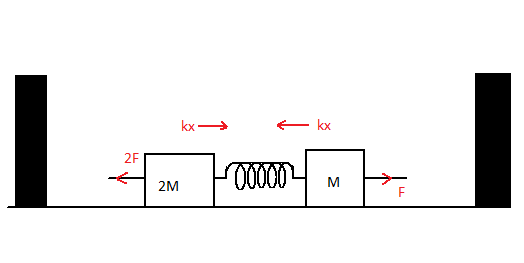
During this, the work done in the center of the mass frame will be zero. Therefore we get the total work done equation as \[{W_{spring}} + {W_F} + {W_{2F}} = 0\]. But, work done is a product of force and displacement for bodies and kinetic energy of springs.

Therefore,
$
  {W_{spring}} + {W_F} + {W_{2F}} = 0 \\
   \Rightarrow \dfrac{1}{2}kx_{max}^2 + F{x_1} + 2F{x_2} = 0 \\
 $
Cancelling out the force factors we get,
${x_{max}} = {x_1} + {x_2}$
According to the given data, the masses of the two bodies are $M$ and $2M$.
Therefore we can write it as \[{M_{x1}} = 2{M_{x2}}\]
Upon reduction we get,
\[
  {M_{x1}} = 2{M_{x2}} \\
   \Rightarrow {x_1} = 2{x_2} \\
 \]
Substituting the value of \[{x_1}\] in the displacement equation we get,
\[
  2{x_2} + {x_2} = {x_{max}} \\
  {x_2} = \dfrac{{{x_{max}}}}{3},{x_1} = \dfrac{2}{3}{x_{max}} \\
 \]
Substituting these values of \[{x_1}\] and \[{x_2}\] in the total energy equation of the system at rest we get,
$
  \dfrac{1}{2}kx_{max}^2 + F{x_1} + 2F{x_2} = 0 \\
   \Rightarrow \dfrac{1}{2}kx_{max}^2 + F(\dfrac{2}{3}{x_{max}}) + 2F(\dfrac{{{x_{max}}}}{3}) = 0 \\
   \Rightarrow \dfrac{1}{2}kx_{max}^2 = \dfrac{{4F}}{3}{x_{max}} \\
   \Rightarrow {x_{max}} = \dfrac{{8F}}{{3k}} \\
 $
In conclusion, the correct option is A.

Note: We must consider the boundary condition of rest at maximum separation. Because at that point, the whole system becomes static and then due to restoring force of the spring, it starts regaining its original position. Also, the work done by spring is negative as it is opposite to the direction of the separation pull force.