
In triangle ABC, right-angled at B, if $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$, find the value of:
i) $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$
ii) $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$
Answer
232.8k+ views
Hint: Use the right-angle triangle Pythagoras theorem. Find the values of $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ and $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$. Right angle means the angle is $90^\circ $. It consists of six trigonometric ratios such as $sin, cos, tan, cot, sec$ and $cosec$.
Complete step by step solution:
We know from the problem that $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$.
With the help of above information we can draw the right-angle triangle as we know that tan A is the ratio of perpendicular and base of a right angled triangle.
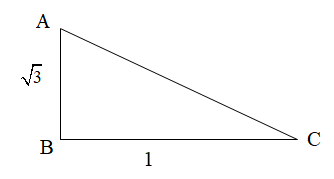
Now, apply the right-angle triangle Pythagoras theorem for the above triangle.
${\left( {{\rm{Hypotenuse}}} \right)^2} = {\left( {{\rm{Height}}} \right)^2} + {\left( {{\rm{Base}}} \right)^2}\\
{\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$
Substitute the values from the above diagram \[{\rm{AB}} = \sqrt 3\] and \[{\rm{BC}} = 1\] in ${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$.
${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}\\
= {\left( {\sqrt 3 } \right)^2} + {\left( 1 \right)^2}\\
= 3 + 1\\
= 4$
We can take the square root of the above equation.
${\rm{AC}} = \sqrt 4 \\
= 2$
Hence, the hypotenuse of the triangle from the above result is 2.
Now we also calculate the value of $\sin {\rm{A}}$ from the formula below.
$\sin {\rm{A}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\sin {\rm{A}}$ from the above result is $\dfrac{1}{2}$.
Now, we also calculate the value of $\cos {\rm{A}}$ from the formula below.
$\cos {\rm{A}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\cos {\rm{A}}$ from the above result is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\sin {\rm{C}}$:
$\sin {\rm{C}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\sin {\rm{C}}$ is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\cos {\rm{C}}$:
$\cos {\rm{C}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\cos {\rm{C}}$ is $\dfrac{1}{2}$.
(i) Solve the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
$\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{1}{2}} \right)\left( {\dfrac{1}{2}} \right) + \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{1}{4} + \dfrac{3}{4}\\
= \dfrac{4}{4}\\
= 1$
Hence, the value of the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ is 1.
(ii) Solve the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
$cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{1}{2}} \right) - \left( {\dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{{\sqrt 3 }}{4} - \dfrac{{\sqrt 3 }}{4}\\
= 0
$
Hence, the value of the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$ is 0.
Note: Here we use the Pythagoras theorem to solve the trigonometric values such as $\sin {\rm{A }}$ and $\cos{\rm{A}}$. The trigonometric values cosec, sec and cot are the opposite values of sin, cos and tan respectively.
Complete step by step solution:
We know from the problem that $tan{\rm{A}} = \dfrac{1}{{\sqrt 3 }}$.
With the help of above information we can draw the right-angle triangle as we know that tan A is the ratio of perpendicular and base of a right angled triangle.
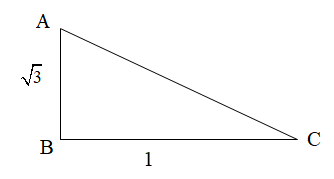
Now, apply the right-angle triangle Pythagoras theorem for the above triangle.
${\left( {{\rm{Hypotenuse}}} \right)^2} = {\left( {{\rm{Height}}} \right)^2} + {\left( {{\rm{Base}}} \right)^2}\\
{\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$
Substitute the values from the above diagram \[{\rm{AB}} = \sqrt 3\] and \[{\rm{BC}} = 1\] in ${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}$.
${\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^{\rm{2}}}\\
= {\left( {\sqrt 3 } \right)^2} + {\left( 1 \right)^2}\\
= 3 + 1\\
= 4$
We can take the square root of the above equation.
${\rm{AC}} = \sqrt 4 \\
= 2$
Hence, the hypotenuse of the triangle from the above result is 2.
Now we also calculate the value of $\sin {\rm{A}}$ from the formula below.
$\sin {\rm{A}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\sin {\rm{A}}$ from the above result is $\dfrac{1}{2}$.
Now, we also calculate the value of $\cos {\rm{A}}$ from the formula below.
$\cos {\rm{A}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\cos {\rm{A}}$ from the above result is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\sin {\rm{C}}$:
$\sin {\rm{C}} = \dfrac{{{\rm{Base}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\\
= \dfrac{{\sqrt 3 }}{2}$
Hence, the value of $\sin {\rm{C}}$ is $\dfrac{{\sqrt 3 }}{2}$.
Now, calculate the value of $\cos {\rm{C}}$:
$\cos {\rm{C}} = \dfrac{{{\rm{Height}}}}{{{\rm{Hypotenuse}}}}\\
= \dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\\
= \dfrac{1}{2}$
Hence, the value of $\cos {\rm{C}}$ is $\dfrac{1}{2}$.
(i) Solve the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$.
$\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{1}{2}} \right)\left( {\dfrac{1}{2}} \right) + \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{1}{4} + \dfrac{3}{4}\\
= \dfrac{4}{4}\\
= 1$
Hence, the value of the trigonometric relation $\sin {\rm{A}}\cos {\rm{C}} + \cos {\rm{A}}\sin {\rm{C}}$ is 1.
(ii) Solve the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
Substitute the values $\sin {\rm{A}} = \dfrac{1}{2},\cos {\rm{A}} = \dfrac{{\sqrt 3 }}{2},\sin {\rm{C}} = \dfrac{{\sqrt 3 }}{2},{\rm{ and }}\cos {\rm{C}} = \dfrac{1}{2}$ in $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$.
$cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}} = \left( {\dfrac{{\sqrt 3 }}{2}} \right)\left( {\dfrac{1}{2}} \right) - \left( {\dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right)\\
= \dfrac{{\sqrt 3 }}{4} - \dfrac{{\sqrt 3 }}{4}\\
= 0
$
Hence, the value of the trigonometric relation $cos{\rm{A}}\cos {\rm{C}} - \sin {\rm{A}}\sin {\rm{C}}$ is 0.
Note: Here we use the Pythagoras theorem to solve the trigonometric values such as $\sin {\rm{A }}$ and $\cos{\rm{A}}$. The trigonometric values cosec, sec and cot are the opposite values of sin, cos and tan respectively.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding the Electric Field of a Uniformly Charged Ring

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions For Class 11 Maths Chapter 12 Limits and Derivatives (2025-26)

NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections (2025-26)

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




