




Step-by-Step Guide: Applying the Triangle Law to Solve Vector Problems
The triangle law of vector addition establishes a geometric method for obtaining the resultant of two vectors by constructing a triangle whose sides represent their magnitudes and directions.
Formal Statement and Diagrammatic Representation of the Triangle Law of Vector Addition
Definition: If two vectors are represented in magnitude and direction by two sides of a triangle taken in order, their resultant is represented by the third side of the triangle taken in the reverse order. If $\vec{A}$ and $\vec{B}$ are the two vectors, then the resultant $\vec{R}$ is given by $\vec{R} = \vec{A} + \vec{B}$. The tail of $\vec{B}$ is placed at the head of $\vec{A}$, and $\vec{R}$ is drawn from the tail of $\vec{A}$ to the head of $\vec{B}$.
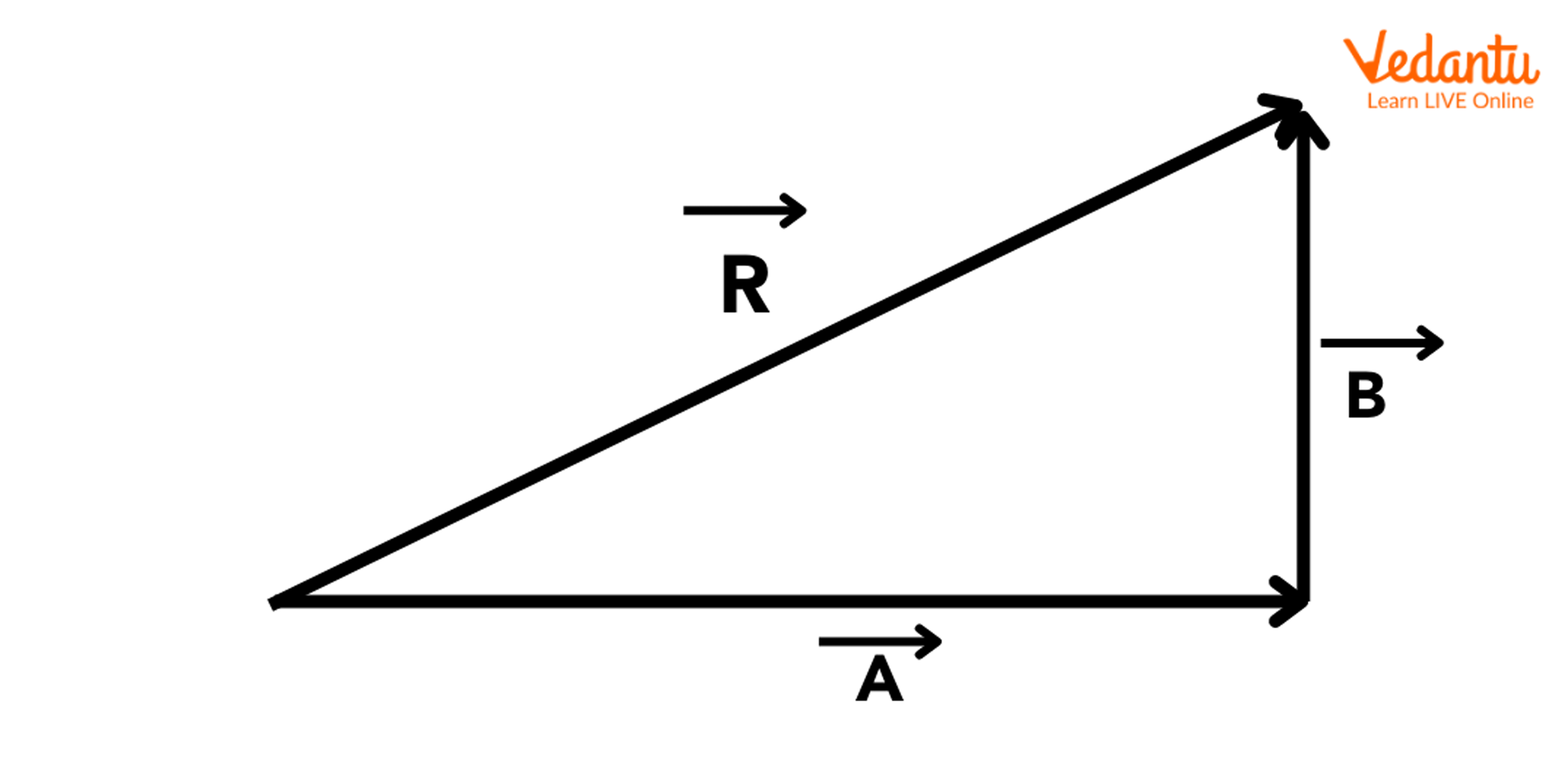
In this construction, $\vec{A}$ and $\vec{B}$ must be arranged such that their directions and magnitudes are preserved, maintaining vector equivalence through translation. For foundational definitions and operations, see Introduction to Vector Algebra.
Standard Formulae for Magnitude and Direction of the Resultant
Let vectors $\vec{A}$ and $\vec{B}$ make an angle $\theta$ with each other. The magnitude of the resultant vector $\vec{R}$ by the triangle law is
$|\vec{R}| = \sqrt{A^2 + B^2 + 2AB\cos\theta}$
The direction of $\vec{R}$, measured as angle $\phi$ from $\vec{A}$, is given by
$\phi = \tan^{-1} \left( \dfrac{B\sin\theta}{A+B\cos\theta} \right)$
These equations remain valid for all pairs of non-zero vectors, provided the included angle $\theta$ is well-defined and measured from $\vec{A}$ towards $\vec{B}$.
Derivation of Resultant Expression Using Triangle Construction
Consider $\vec{A}$ represented by segment $OA$ and $\vec{B}$ by segment $AB$, forming triangle $OAB$. Extend $OA$ to $C$ such that $BC$ is perpendicular to $OC$, and let $\theta$ be the angle between $\vec{A}$ and $\vec{B}$.
In $\triangle OBC$ (right-angled at $B$), apply the Pythagorean theorem:
$OB^2 = OC^2 + BC^2$
Express $OC$ and $BC$ in terms of $A$, $B$, and $\theta$ using triangle $ABC$:
$AC = B\cos\theta$, $BC = B\sin\theta$, $OC = OA + AC = A + B\cos\theta$
Substitute into the Pythagorean identity:
$\begin{aligned} R^2 = (A + B\cos\theta)^2 + (B\sin\theta)^2 \end{aligned}$
Expand and simplify step by step:
$\begin{aligned} R^2 &= A^2 + 2AB\cos\theta + B^2\cos^2\theta + B^2\sin^2\theta \\ &= A^2 + 2AB\cos\theta + B^2(\cos^2\theta + \sin^2\theta) \\ &= A^2 + 2AB\cos\theta + B^2 \end{aligned}$
Thus, $R = \sqrt{A^2 + 2AB\cos\theta + B^2}$ as required. Result: The formula expresses the resultant’s magnitude when two vectors are joined sequentially.
For the direction $\phi$:
$\tan\phi = \dfrac{BC}{OC} = \dfrac{B\sin\theta}{A+B\cos\theta}$
Therefore, $\phi = \tan^{-1} \left( \dfrac{B\sin\theta}{A+B\cos\theta} \right)$ gives the angle between $\vec{A}$ and $\vec{R}$.
Specific Cases and Geometric Consequences
If $\theta = 0^\circ$, the vectors are collinear and point in the same direction; $|\vec{R}| = A + B$.
If $\theta = 180^\circ$, the vectors are opposite; $|\vec{R}| = |A - B|$.
If $\theta = 90^\circ$, the vectors are perpendicular; $|\vec{R}| = \sqrt{A^2 + B^2}$.
Difference Between Vectors and Scalars clarifies relevant distinctions for these limiting scenarios.
Illustrative Problems Based on the Triangle Law of Vector Addition
Example: Two vectors, $\vec{P}$ and $\vec{Q}$, have magnitudes $6$ units and $8$ units, respectively. The angle between them is $60^{\circ}$. Find the magnitude and direction of their resultant.
Solution: Given $P = 6$, $Q = 8$, $\theta = 60^\circ$.
$R = \sqrt{P^2 + Q^2 + 2PQ\cos\theta}$
$= \sqrt{6^2 + 8^2 + 2 \times 6 \times 8 \times 0.5}$
$= \sqrt{36 + 64 + 48}$
$= \sqrt{148}$
$= 12.165$ units
Direction:
$\phi = \tan^{-1} \left( \dfrac{8 \times \sin 60^\circ}{6 + 8 \times \cos 60^\circ} \right)$
$= \tan^{-1} \left( \dfrac{8 \times 0.866}{6 + 8 \times 0.5} \right)$
$= \tan^{-1} \left( \dfrac{6.928}{10} \right)$
$= \tan^{-1} (0.6928)$
$= 34.7^\circ$
Result: The resultant’s magnitude is $12.165$ units and it is at $34.7^\circ$ with respect to $\vec{P}$.

Example: If the magnitudes of two vectors are $9$ units and $4$ units and the resultant magnitude is $11$ units, find the angle between the vectors.
Solution: Let $A=9$, $B=4$, $R=11$.
$R^2 = A^2 + B^2 + 2AB\cos\theta$
$121 = 81 + 16 + 72\cos\theta$
$121 - 97 = 72\cos\theta$
$24 = 72\cos\theta$
$\cos\theta = \dfrac{24}{72} = \dfrac{1}{3}$
$\theta = \cos^{-1}(\dfrac{1}{3}) \approx 70.53^\circ$
Result: The vectors are approximately at $70.53^\circ$ to each other.
Example: Two vectors, each of magnitude $a$, are perpendicular. Determine the resultant’s magnitude and orientation with respect to the first vector.
Solution: $A = a$, $B = a$, $\theta = 90^\circ$.
$R = \sqrt{a^2 + a^2 + 2a^2 \times 0} = \sqrt{2}a$
$\phi = \tan^{-1} \left( \dfrac{a}{a} \right) = \tan^{-1}(1) = 45^\circ$
Result: The resultant has magnitude $\sqrt{2}a$ and direction $45^\circ$ from the first vector.
Example: Calculate the resultant of vectors $\vec{A}$ and $\vec{B}$ both of magnitude $5$ units, but opposite in direction.
Solution: $A=5$, $B=5$, $\theta = 180^\circ$.
$R = \sqrt{5^2 + 5^2 + 2\times 5 \times 5 \times (-1)}$
$= \sqrt{25 + 25 - 50}$
$= \sqrt{0} = 0$
Result: The resultant vector is the zero vector when two equal and opposite vectors are added.
For more graphical methods of vector addition or advanced examples, see Graphical Methods of Vector Addition.
Exam Cues and Common Misconceptions Related to the Triangle Law of Vector Addition
- Vectors must be translated, not rotated, for head-to-tail arrangement
- Angle $\theta$ must be properly defined between vectors
- Direction formula gives angle with respect to the first vector always
- Triangle law is exclusive to the addition of two vectors
- Graphical and algebraic forms must yield the same resultant
Component form and parallelogram law interpretations are mathematically equivalent to the triangle method for two vectors; see Understanding Vector Triple Product for multi-vector product operations.
FAQs on What Is the Triangle Law of Vector Addition?
1. What is the triangle law of vector addition?
The triangle law of vector addition states that when two vectors are represented as two sides of a triangle taken in order, their sum is given by the third side taken in the opposite order. To apply the triangle law:
- Draw vector A as an arrow.
- From the head of A, draw vector B in the same scale and direction.
- The resultant vector R is drawn from the tail of A to the head of B.
2. State and explain the triangle law of vector addition with the help of a diagram.
The triangle law of vector addition states that if two vectors are represented as two sides of a triangle taken in order, the third side taken in the opposite order gives their sum.
- Step 1: Draw vector AB.
- Step 2: From point B, draw vector BC.
- Step 3: The vector AC (from A to C) represents the resultant vector.
3. What is the resultant of two vectors according to the triangle law?
According to the triangle law, the resultant of two vectors is the vector drawn from the tail of the first to the head of the second vector.
- The resultant (R) is represented by the side of the triangle opposite to the vector addition sequence.
- If →AB = A and →BC = B, then →AC = R = A + B.
4. How do you apply the triangle law of vector addition in numerical problems?
The triangle law is applied in numerical problems to calculate the resultant vector when two vectors are given. The steps to apply are:
- Draw the first vector to scale and direction.
- From its head, draw the second vector to scale and direction.
- Join the tail of the first vector to the head of the second; this is the resultant.
- Use the law of cosines if vectors are not at a right angle:
R = √(A^2 + B^2 + 2ABcosθ)
5. What are the conditions for applying the triangle law of vector addition?
The triangle law of vector addition can be applied when:
- Two vectors are given in both magnitude and direction.
- The vectors are represented as two continuous sides of a triangle taken in order.
- Their magnitudes and directions can be accurately drawn.
6. What is the difference between the triangle law and the parallelogram law of vector addition?
The triangle law and the parallelogram law are both methods for vector addition, but they differ in construction:
- Triangle Law: Vectors are placed tip-to-tail; the third side represents the resultant.
- Parallelogram Law: Both vectors start from a common point; the diagonal of the parallelogram represents the resultant.
7. Why is the triangle law of vector addition important in physics?
The triangle law of vector addition is important in physics because it provides a graphical and analytical way to add vectors, which are essential in determining resultant forces, velocities, and other vector quantities.
- Helps in adding displacement, force, and velocity vectors.
- Essential in solving equilibrium and motion problems.
- Used in CBSE and other exam syllabi for problem-solving techniques.
8. Can the triangle law be used for more than two vectors? Explain.
The triangle law is directly applicable only to two vectors at a time, but can be extended to more vectors using the polygon law:
- For more than two vectors, place each one tip-to-tail in sequence.
- The resultant is drawn from the tail of the first to the head of the last vector.
9. Is the triangle law of vector addition commutative?
Yes, the triangle law of vector addition is commutative.
- Order of addition does not affect the resultant: A + B = B + A.
- The shape of the triangle may change, but the resultant remains the same.
10. Give an example illustrating the triangle law of vector addition.
Example: If vector A = 5 N east and vector B = 3 N north, the resultant using the triangle law is found by:
- Drawing 5 N east as an arrow.
- From its head, drawing 3 N north.
- Joining the tail of the first vector to the head of the second forms the resultant.
- Use Pythagoras' theorem if angle is 90°: Resultant = √(5^2 + 3^2) = 5.83 N.
11. What is meant by the resultant of two vectors?
The resultant of two vectors is a single vector which has the same effect as the combined effect of the two vectors when applied together.
- It represents magnitude and direction resulting from vector addition.
- It is determined using laws like the triangle law or parallelogram law.
12. How is the magnitude of the resultant calculated if the angle between two vectors is known?
If two vectors A and B make an angle θ between them, the magnitude of their resultant R is calculated using:
- R = √(A^2 + B^2 + 2ABcosθ)

































