Question

Minimum area of the circle which touches the parabolas $y={{x}^{2}}+1$ and ${{y}^{2}}=x-1$ is
(a) \[\dfrac{9\pi }{16}\] sq. units
(b) \[\dfrac{9\pi }{32}\] sq. units
(c) \[\dfrac{9\pi }{8}\] sq. units
(d) \[\dfrac{9\pi }{4}\] sq. units

Answer 1

Hint: Observe that the two parabolas are symmetric with respect to the line $y=x$ and thus, the tangents will be parallel to the line $y=x$. Use this fact to write the slope of tangents at points at which the circle touches the parabola. Equate the slope of these tangents to 1 and solve the equations to find the coordinates of point of intersection of circle and parabola. Calculate the diameter of the circle using distance formula and then calculate the area of the circle.

Complete step-by-step solution -

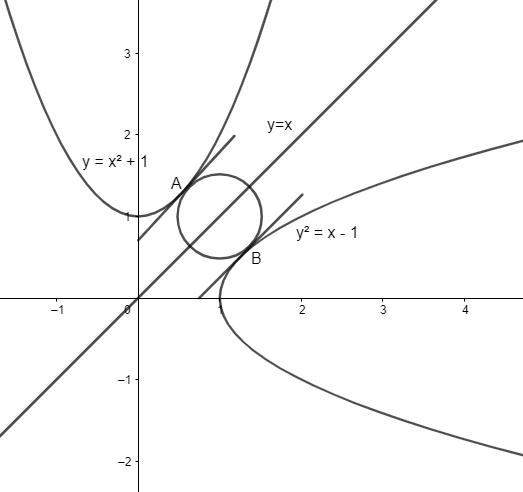
We have two parabolas $y={{x}^{2}}+1$ and ${{y}^{2}}=x-1$.
Let’s assume that the equation of our required circle is \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{a}^{2}}\].
Consider the parabola \[y={{x}^{2}}+1\].
If we replace y by x and x by y in the above equation of parabola, we get \[x={{y}^{2}}+1\] which is the equation of our second parabola.
So, the two parabolas are symmetric with respect to the line \[y=x\].
Let’s assume that our circle touches the parabola \[x={{y}^{2}}+1\] at point A and the parabola \[y={{x}^{2}}+1\] at point B.
So, the tangent at point A and B is parallel to the line. Thus, their slopes are the same, i.e., 1.

We will now find the slope of two lines.
The slope of any line is \[\dfrac{dy}{dx}\].
Thus, the slope of tangent at A is \[\dfrac{dy}{dx}=2x\], as \[y={{x}^{2}}+1\]. As the slope of the tangent is 1, we have $2x=1$.
Rearranging the terms of the above equation, we have $x=\dfrac{1}{2}$.
Substituting the above value of x in the equation \[y={{x}^{2}}+1\], we get \[y={{\left( \dfrac{1}{2} \right)}^{2}}+1=\dfrac{5}{4}\].
Thus, the coordinates of A are \[\left( \dfrac{1}{2},\dfrac{5}{4} \right)\].
Similarly, the slope of tangent at B is $\dfrac{dy}{dx}=\dfrac{1}{2\sqrt{x-1}}$, as \[{{y}^{2}}=x-1\Rightarrow y=\sqrt{x-1}\].
As the slope of the tangent is 1, we have $\dfrac{1}{2\sqrt{x-1}}=1$.
Simplifying the above equation, we have $2\sqrt{x-1}=1\Rightarrow \sqrt{x-1}=\dfrac{1}{2}$.
$\Rightarrow x-1={{\left( \dfrac{1}{2} \right)}^{2}}=\dfrac{1}{4}$
Thus, we have $x=1+\dfrac{1}{4}=\dfrac{5}{4}$.
Substituting the value of x in the equation \[y=\sqrt{x-1}\], we get \[y=\sqrt{\dfrac{5}{4}-1}=\pm \dfrac{1}{2}\].
But as B lies in the first quadrant, we reject \[y=-\dfrac{1}{2}\].
Thus the coordinates of B are \[\left( \dfrac{5}{4},\dfrac{1}{2} \right)\].
Now, we know AB forms the diameter of the circle.
We know that the distance between two points with coordinates \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\].
Substituting \[{{x}_{1}}=\dfrac{1}{2},{{y}_{1}}=\dfrac{5}{4},{{x}_{2}}=\dfrac{5}{4},{{y}_{2}}=\dfrac{1}{2}\], we get length of AB as \[\sqrt{{{(\dfrac{1}{2}-\dfrac{5}{4})}^{2}}+{{(\dfrac{5}{4}-\dfrac{1}{2})}^{2}}}=\sqrt{{{\left( \dfrac{-3}{4} \right)}^{2}}+{{\left( \dfrac{3}{4} \right)}^{2}}}=\sqrt{\dfrac{9}{16}+\dfrac{9}{16}}=\sqrt{\dfrac{9}{8}=}\dfrac{3}{4}\sqrt{2}\] units.
We know the area of the circle with diameter d is \[\pi \dfrac{{{d}^{2}}}{4}\] sq. units.
Substituting \[d=\dfrac{3}{4}\sqrt{2}\], the required area is \[=\dfrac{\pi }{4}{{\left( \dfrac{3\sqrt{2}}{4} \right)}^{2}}=\dfrac{18\pi }{64}=\dfrac{9\pi }{32}\] sq. units.
Hence, the area of the circle is \[\dfrac{9\pi }{32}\] sq. units, which is option (b).

Note: We can also use the formula of reflection of a point with respect to a line to check that the two parabolas are symmetric with respect to the line by reflecting the focus of one parabola along the line to get the focus of another parabola. If we are calculating the area of circle using the diameter of circle, use the formula $\pi \dfrac{{{d}^{2}}}{4}$ and if we are calculating the area of circle using radius of circle, use the formula $\pi {{r}^{2}}$.