




How Does Gravitational Field Relate to Gravitational Potential?
The relationship between gravitational field and potential is a fundamental concept in physics, relevant for solving various types of problems in gravitation. Understanding this relation allows for the calculation of gravitational effects on masses in fields around objects like Earth, planets, and stars. This concept is essential for success in exams such as JEE, where both definitions and derivations are frequently tested.
Newton’s Law of Universal Gravitation and Gravitational Field
Newton’s law of universal gravitation states that every pair of masses $M_1$ and $M_2$, separated by a distance $R$, attract each other with a force given by $F = G \dfrac{M_1 M_2}{R^2}$, where $G$ is the universal gravitational constant. This force acts along the line joining the centres of the two bodies.
The gravitational field at a point is defined as the force experienced by a unit mass placed at that point. For a mass $M$ at a distance $r$, the magnitude of gravitational field $E$ at that point is $E = \dfrac{GM}{r^2}$. The direction is always towards the mass producing the field.
The unit of gravitational field is $\mathrm{N\,kg^{-1}}$, which is equivalent to an acceleration ($\mathrm{m\,s^{-2}}$). Detailed study of these concepts can be found in Understanding Gravitation.
Gravitational Potential and Its Definition
Gravitational potential at a point is defined as the work done to bring a unit mass from infinity to that point in the gravitational field. For a mass $M$, the gravitational potential $V$ at a distance $r$ from its centre is $V = -\dfrac{GM}{r}$. The negative sign indicates the attractive nature of gravity.
The SI unit of gravitational potential is $\mathrm{J\,kg^{-1}}$. Gravitational potential measures the potential energy per unit mass at a certain point in the field. Full details on gravitational potential energy are available in Gravitational Potential Energy.
Derivation: Relation Between Gravitational Field and Potential
Consider a mass $m$ moved from point $A$ to point $B$ in a gravitational field. The work done by the field is $dW = F \cdot dr = mE \cdot dr$, where $dr$ is a small displacement in the field direction.
For conservative forces such as gravity, $dU = -dW$. The change in gravitational potential energy $dU$ equals $-mE \cdot dr$, and the corresponding change in potential is $dV = \dfrac{dU}{m} = -E \cdot dr$.
Therefore, the relation is expressed as:
$\displaystyle E = -\dfrac{dV}{dr}$
This means the gravitational field at any point is equal to the negative gradient of gravitational potential at that point. In vector form, $\vec{E} = -\nabla V$.
| Quantity | Expression |
|---|---|
| Gravitational field $E$ | $\dfrac{GM}{r^2}$ |
| Gravitational potential $V$ | $-\dfrac{GM}{r}$ |
| Relationship | $E = -\dfrac{dV}{dr}$ |
Relation Between Gravitational Field and Potential Energy
The gravitational potential energy $U$ of a mass $m$ at a distance $r$ from mass $M$ is $U = mV$, where $V$ is the gravitational potential at that point. Hence, $U = -\dfrac{GMm}{r}$. This is discussed further in Gravitational Potential Energy.
Gravitational Field and Potential Due to Spherical Mass
For a uniform solid sphere of mass $M$ and radius $a$, the gravitational field and potential vary depending on the location (outside, on the surface, or inside the sphere).
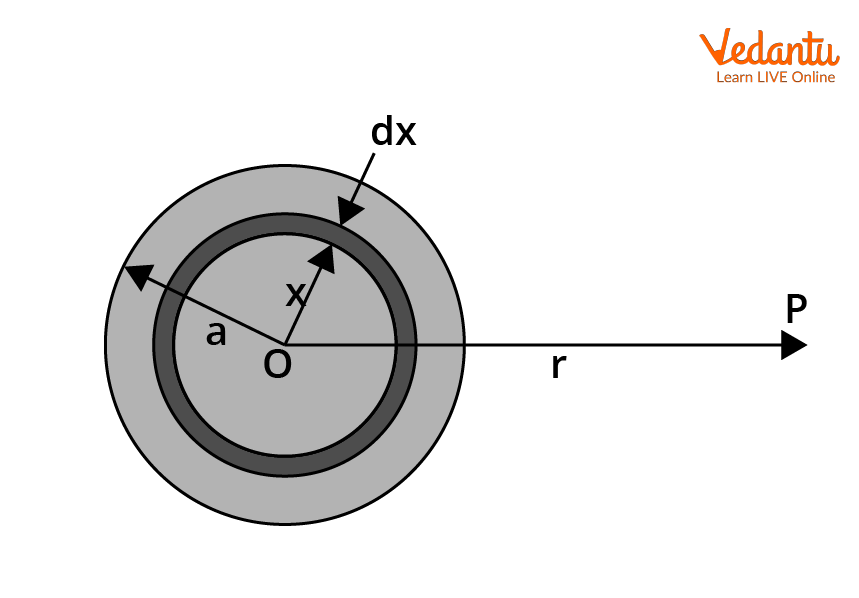
For a point outside the sphere ($r \geq a$):
Gravitational field: $E = \dfrac{GM}{r^2}$
Gravitational potential: $V = -\dfrac{GM}{r}$
For a point on the surface ($r = a$):
$E = \dfrac{GM}{a^2}$, $V = -\dfrac{GM}{a}$
For a point inside the uniform solid sphere ($r < a$):
$E = \dfrac{GM r}{a^3}$
$V = -\dfrac{GM}{2a^3}(3a^2 - r^2)$
The potential inside a sphere varies quadratically with $r$, while the field increases linearly with $r$ up to the surface. This variation is important in planetary and stellar physics, and for exam preparation such as with Gravitation Revision Notes.
Solved Example: Calculating Field from Potential
Given the gravitational potential at a point is $V = -2 \times 10^7\,\mathrm{J\,kg^{-1}}$, and the potential at a nearby point $0.5\,\mathrm{m}$ away is $V' = -1.8 \times 10^7\,\mathrm{J\,kg^{-1}}$, calculate the field.
- Potential difference $\Delta V = V' - V = 0.2 \times 10^7\,\mathrm{J\,kg^{-1}}$
- Distance $\Delta r = 0.5\,\mathrm{m}$
- Field $E = -\dfrac{\Delta V}{\Delta r} = -\dfrac{0.2 \times 10^7}{0.5} = -4 \times 10^6\,\mathrm{N\,kg^{-1}}$
Thus, the gravitational field between the two points is $4 \times 10^6\,\mathrm{N\,kg^{-1}}$, directed towards the mass producing the field.
Key Points on Gravitational Field and Potential Relations
- Gravitational field is the negative derivative of potential with respect to distance
- Both field and potential are central for solving gravitation problems
- Potential is scalar; field is vector
- The field points in the direction of decreasing potential
- Integration of field gives potential difference
Further practice on these concepts can be found in the Gravitation Practice Paper.
Summary: Importance of the Relationship
The derivation $E = -\dfrac{dV}{dr}$ links the vector property of gravitational field to the scalar characteristic of gravitational potential. Mastery of this relationship is essential for advanced gravitation concepts and numerical problem solving. For acceleration-related details, refer to Acceleration Due to Gravity.
FAQs on Understanding the Relation Between Gravitational Field and Potential
1. What is the relation between gravitational field and potential?
The relation between gravitational field and potential shows how the gravitational field strength is the negative gradient of gravitational potential.
- Gravitational field (E) at a point is equal to the negative rate of change of gravitational potential (V) with distance.
- The mathematical relation is: E = -dV/dr, where 'E' is the field, 'V' is potential, and 'r' is distance.
- This implies that the field points in the direction where potential decreases most rapidly.
2. How do you express gravitational field in terms of potential?
Gravitational field (E) is given by the negative gradient of gravitational potential (V):
- E = -dV/dr, meaning the field at a point is the rate at which potential changes with distance, taken negatively.
- This formula helps you calculate field strength from knowledge of potential.
- It also indicates the field is highest where potential changes steeply.
3. What is gravitational potential?
Gravitational potential at a point is the work done to bring unit mass from infinity to that point against gravity.
- It is measured in joules per kilogram (J/kg).
- Higher (less negative) potential means less energy required to reach that location from infinity.
4. Define gravitational field and its SI unit.
Gravitational field is the region where an object experiences a force due to gravity of another mass, and its SI unit is N/kg.
- It represents force per unit mass exerted at any point.
- Also expressed as acceleration due to gravity (m/s²).
5. What is the mathematical relationship between gravitational field and gravitational potential for a point mass?
For a point mass, the gravitational field and potential are related as follows:
- Potential at distance r: V = -GM/r
- Field at distance r: E = -dV/dr = -d(-GM/r)/dr = GM/r²
- Here, G is the gravitational constant, M is the mass, and r is the distance from mass.
6. Why is gravitational field the negative gradient of gravitational potential?
Gravitational field is the negative gradient of gravitational potential because field points in the direction of greatest decrease in potential.
- The 'negative' ensures correct direction, as field lines move from higher to lower potential.
- This links the concept of field strength directly with spatial variations in potential.
7. Is gravitational field always negative when related to potential?
The sign of gravitational field derived from potential indicates direction, not necessarily negativity.
- E = -dV/dr shows field direction towards mass (decreasing potential).
- Field points radially inward, so the negative gradient matches gravitational attraction.
8. Explain the physical significance of the negative sign in E = -dV/dr.
The negative sign in E = -dV/dr indicates that the gravitational field points towards decreasing potential.
- This reflects the attractive nature of gravity—objects move toward lower potential energy.
- It also helps in determining field direction in numerical and vector problems.
9. How does gravitational field differ from gravitational potential?
Gravitational field describes force per unit mass (vector), while gravitational potential describes work per unit mass (scalar).
- Field is a vector quantity pointing towards the mass source.
- Potential is a scalar, negative everywhere due to attractive force.
- Field tells about acceleration, potential about energy.
10. Can gravitational field be zero where potential is not zero?
Gravitational field can be zero at certain points even when potential is not zero.
- This occurs at points of equilibrium between multiple attracting masses.
- Potential may have a value, but its gradient (field) can be zero due to cancellation of forces.
11. What is the SI unit and dimensional formula of gravitational potential?
The SI unit of gravitational potential is joule per kilogram (J/kg), and its dimensional formula is [L² T⁻²].
- It denotes energy per unit mass.
- Gravitational potential is always negative near a massive body due to its attractive nature.
12. How do you calculate gravitational field from a given potential function?
To calculate gravitational field from a potential function, take the negative derivative of potential with respect to distance.
- If V(r) is given, then E(r) = -dV/dr.
- For multidimensional cases, use the gradient: E = -∇V.

































