Question

What is the position and nature of the image formed by the lens combined shown in the figure?
(${f_1},{f_2}$ are focal length)

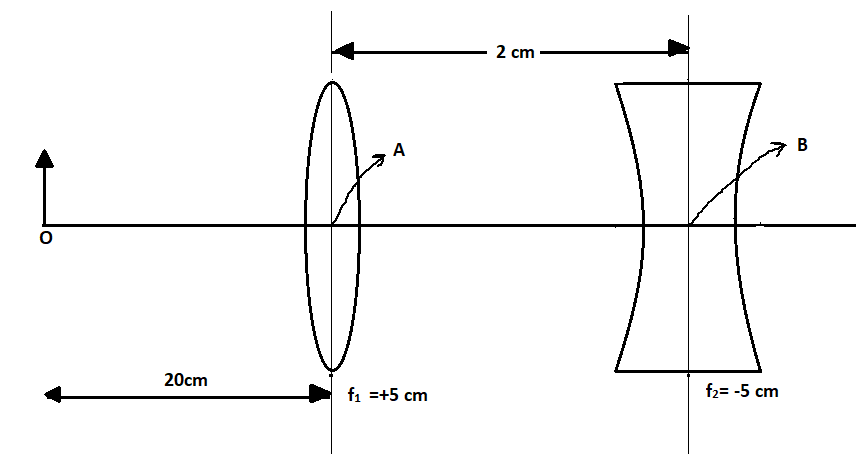
A) $70cm$from point B at left; virtual
(B) $40cm$ from point B at right; real
(C) $\dfrac{{20}}{3}cm$ from point B at right, real
(D) $70cm$ from point B at right, real

Answer 1

Hint: Recall the lens formula, object distance, image distance? Properties of the convex and concave lens? How can we decide the nature of the lens? On what factors the nature of the lens depends? What are the convex and concave lenses? Difference between the convex and concave lens?

Formula Used:
Lens formula, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where, $v$ is the image distance from the lens
$u$ is the object distance from the lens
$f$ is the focal length of the lens

Complete step by step answer:
In the question focal lengths of both lens are given by,
${f_1} = 5cm$ , focal length of the first lens
${f_2} = - 5cm$ , focal length of the second lens
For the first lens that is convex,
The object distance is given as,
$u = - 20cm$
The lens formula is given by,
Lens formula, $\dfrac{1}{{{v_1}}} - \dfrac{1}{{{u_1}}} = \dfrac{1}{{{f_1}}}$
Where, ${v_1}$ is the image distance from the first lens
${u_1}$ is the object distance from the first lens
${f_1}$ is the focal length of the first lens
On putting values of all the given variables, we get
\[ \Rightarrow \dfrac{1}{{{v_1}}} - \dfrac{1}{{ - 20}} = \dfrac{1}{5}\]
On further solving we get,
$ \Rightarrow {v_1} = \dfrac{{20}}{3}cm$
Distance between two lens is given in the question as $2cm$
So, the image formed by the convex lens works as the object for the concave lens
Now, object distance for the second lens is given by,
${u_2} = \dfrac{{20}}{3} - 2$
$ \Rightarrow {u_2} = \dfrac{{14}}{3}cm$
We know that the lens formula is given by,
$\dfrac{1}{{{v_2}}} - \dfrac{1}{{{u_2}}} = \dfrac{1}{{{f_2}}}$
Where, ${v_2}$ is the image distance from the second lens
${u_2}$ is the object distance from the second lens
${f_2}$ is the focal length of the second lens
On putting the values of all the available variables, we get
\[ \Rightarrow \dfrac{1}{{{v_2}}} - \dfrac{1}{{\dfrac{{14}}{3}}} = \dfrac{1}{{ - 5}}\]
On further solving, we get
${v_2} = 70cm$
As we know that if the value of image distance is positive, a real image is formed and the image formed is $70cm$ from point B at right.

Therefore, the correct option is option (D)

Note:
If image distance $v$ is negative, the image formed is virtual. If image distance $v$ is positive, the image formed is real. The object distance $u$ is always negative as it is on the left side of the lens. The focal length of the convex lens is positive. The focal length of the concave lens is negative.