Question

Show that the locus of the pole, with respect to the auxiliary circle, of a tangent to the ellipse is a similar concentric ellipse, whose major axis is at right angles to that of the original ellipse.

Answer 1

Hint: Firstly, we write the general equation for an ellipse and then the standard form for the polar with respect to the pole of an ellipse. Since it is given that polar given here is tangent to the auxiliary circle. The auxiliary circle is hence drawn concentric with an ellipse and the radius of this auxiliary circle will be half of the major axis. Now find the perpendicular distance from the center to the polar and equate it to the radius of the auxiliary circle. Evaluate further to get a locus of the pole.

Complete step-by-step solution:
The equation of the auxiliary circle can be calculated using the same center of the ellipse and the radius will be equal to the length of the major axis.
Equation of polar with respect to pole $\left( {{x}_{1}},{{y}_{1}} \right)$ for an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is given as $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{2}}}{{{b}^{2}}}=1$
Let the pole P (h, k) inside the ellipse and polar is line L as shown in the diagram.


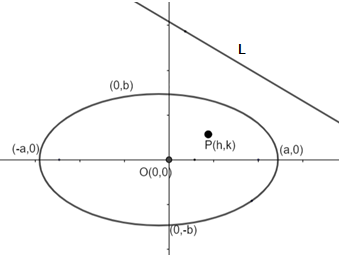
As we know that polar is the line w.r.t pole in the ellipse in such a way that,
There is an infinite number of lines that can be drawn through the pole and each can be termed as a chord and cut at two points to the ellipse. Two of the tangents can be drawn through each chord and ellipse intersection point as shown below.

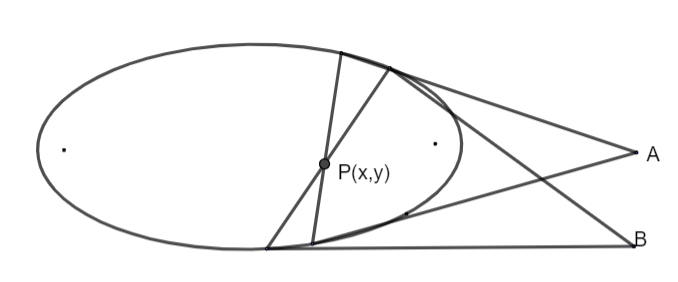
The line joining the points A and B will be termed as polar i.e., all the points we get after drawing two tangents w.r.t P (pole) will lie on a line which is called polar, and the equation of that line is T=0.
The line is given by,
$\Rightarrow \dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$
Now, coming to the question,
The general equation of the ellipse is given as, $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Pole assumed is at the point P (h, k)
Pole w.r.t pole T=0 is given by,
$\Rightarrow \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1$
Hence, the equation of polar w.r.t pole P (h, k) is,
$\Rightarrow \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1$
Let this be equation 1.
As it is given the polar given here is tangent to the auxiliary circle. The Auxiliary circle is drawn concentric with the ellipse and the radius is half of the major axis as shown in the diagram.

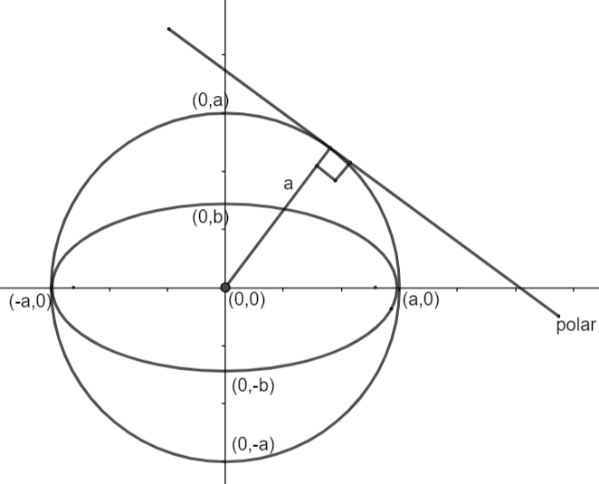
Now, we can observe that radius ‘a’ shown in the figure will be perpendicular to the tangent (polar for an ellipse).
Hence, the perpendicular distance of the polar to the center is a radius.
As we know the formula for calculating the perpendicular distance of any line $Ax+By+C=0$ from any point $\left( {{x}_{1}},{{y}_{1}} \right)$ is,
$\Rightarrow \left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$
Since Radius of circle = Perpendicular distance of polar to center.
We have the equation of polar which is, $\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1$
Comparing the above equation with $Ax+By+C=0$ what we get,
$\Rightarrow A=\dfrac{h}{{{a}^{2}}};B=\dfrac{k}{{{b}^{2}}};C=-1$
Hence, Radius of circle = Perpendicular distance of polar to center.
$\Rightarrow a=\left| \dfrac{0+0-1}{\sqrt{{{\left( \dfrac{h}{{{a}^{2}}} \right)}^{2}}+{{\left( \dfrac{k}{{{b}^{2}}} \right)}^{2}}}} \right|$
$\Rightarrow a=\left| \dfrac{-1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}} \right|$
Squaring both the sides of the above equations, we get
$\Rightarrow {{a}^{2}}=\dfrac{1}{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}$
$\Rightarrow \dfrac{1}{{{a}^{2}}}=\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}$
Replacing (h, k) to (x, y) we get the required locus,
$\Rightarrow \dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{a}^{2}}}$
Now, coming to the second part of the problem,
Equation of the ellipse, we have assumed is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , Whose center is (0, 0).
Hence the locus of pole calculated above is,
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{\dfrac{{{b}^{4}}}{{{a}^{2}}}}=1$
Hence, comparing the above equations with the standard equation of an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , we get that locus of the pole is an ellipse as well with a center (0, 0).
Hence, it is concentric with the assumed ellipse.
Now, we can observe that the major axis of the ellipse assumed is X-axis.
Therefore, $a>b$ or ${{a}^{2}}>{{b}^{2}}$
Multiplying both sides by ${{a}^{2}}$ , in ${{a}^{2}}>{{b}^{2}}$ , we get
$\Rightarrow {{a}^{4}}>{{b}^{2}}{{a}^{2}}$
$\Rightarrow \dfrac{{{a}^{4}}}{{{b}^{2}}}>{{a}^{2}}$
Here, we can observe that the major axis of the locus of the pole (ellipse) is now the y-axis. Hence, the major axis of the assumed ellipse and ellipse by the locus of the pole are perpendicular to each other.

Note: Auxiliary circle for any ellipse is concentric with the ellipse. Term auxiliary circle should be clear for this question and how to write its equation as well. Take care of mod sign while writing the perpendicular distance in solution. One can go wrong while checking the relation between $\dfrac{{{a}^{4}}}{{{b}^{2}}}$ and ${{a}^{2}}$ , so try to relate from the initial level as $a>b$ then ${{a}^{2}}>{{b}^{2}}$ and finally $\dfrac{{{a}^{4}}}{{{b}^{2}}}>{{a}^{2}}$.