Question

State Gauss law in electrostatics. Derive an of electric field expression due an infinitely long straight uniformly charged wire. Draw necessary diagrams.

Answer 1

Hint: In electrostatics, the Gauss’s law states that the total electric flux over any closed surface is ${1 {\left/
 { {1 {{\varepsilon _o}}}} \right.
 } {{\varepsilon _o}}}$ times the total charge that is enclosed by the surface. To find the electric field due to an infinitely long current carrying wire, we need to consider a cylindrical Gaussian surface around it.

Complete Step by Step Solution: The Gauss’s law in electrostatics shows us that there is an important relationship that exists between the total electric flux over any closed surface and the total charge that is enclosed by the surface. It states that the total electric flux over any closed surface is ${1 {\left/
 { {1 {{\varepsilon _o}}}} \right.
 } {{\varepsilon _o}}}$ times the total charge that is enclosed by the surface where ${\varepsilon _o}$ is the permittivity in free space.
The mathematical form of the Gauss’s law is,
$\oint\limits_S {\vec E \cdot d\vec S} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
To derive the expression of the electric field due to an infinitely long charged wire, we consider the following diagram,

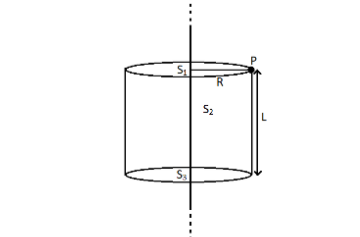
Here we have considered the Gaussian surface as a cylinder that is surrounding the wire which has a surface charge density $\lambda $. This cylinder has a radius $R$ and a length $L$. Let us consider a point P lying on the curved surface of the cylinder. So we need to find the electric field due to the wire at the P.
So, from the Gauss’s law we can write,
$\oint\limits_S {\vec E \cdot d\vec S} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
In the cylinder there are 3 surfaces present as shown in the figure. So we need to find Gauss's law for all the three surfaces ${S_1}$, ${S_2}$ and ${S_3}$.
So we can break the L.H.S. of the integration into three parts as,
$\Rightarrow \int\limits_{{S_1}} {\vec E \cdot d\vec S} + \int\limits_{{S_2}} {\vec E \cdot d\vec S} + \int\limits_{{S_3}} {\vec E \cdot d\vec S} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
Now the direction of the electric field from the wire is radially outwards. So the electric field is perpendicular on the surface ${S_2}$ and is parallel to the surfaces ${S_1}$ and ${S_3}$. So the angle between the electric field and the surface vectors are $90^\circ $ for ${S_1}$ and ${S_3}$, and $0^\circ $ for ${S_2}$as the surface vectors are perpendicular to the surfaces. Therefore, we can write, the dot products in form of the magnitudes as,
$\Rightarrow \int\limits_{{S_1}} {EdS} \cos 90^\circ + \int\limits_{{S_2}} {EdS\cos 0^\circ } + \int\limits_{{S_3}} {EdS\cos 90^\circ } = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
The value of $\cos 0^\circ = 1$ and $\cos 90^\circ = 0$
So the first and the third term of the equation vanish.
Therefore, we get
$\Rightarrow \int\limits_{{S_2}} {EdS} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
Now since the electric field is constant we can take it out of the integration. So,
$\Rightarrow E\int\limits_{{S_2}} {dS} = \dfrac{{{Q_{enc}}}}{{{\varepsilon _o}}}$
The surface integration is over the curved surface of the cylinder. The surface area of the curved surface ${S_2}$ is $\int\limits_{{S_2}} {dS} = 2\pi RL$
And as the surface charge density of the wire is $\lambda $, so the total charge of the wire for $L$ length is,
$\Rightarrow {Q_{enc}} = \lambda L$
So substituting the values,
$\Rightarrow E \times 2\pi RL = \dfrac{{\lambda L}}{{{\varepsilon _o}}}$
The $L$ gets cancelled from both the sides and then taking all the terms except $E$ from the LHS to the RHS we get
\[\Rightarrow E = \dfrac{\lambda }{{2\pi {\varepsilon _o}R}}\]
This is the magnitude of the electric field. The direction of the electric field is radially outwards, so we can write it as
\[\Rightarrow \vec E = \dfrac{\lambda }{{2\pi {\varepsilon _o}R}}\hat R\]

Note: From the formula for the electric field, we can see that it is independent of the length of the wire but depends on the charge density. In case of 3D we need to replace the linear charge density of the wire with its volume charge density.