Question

The points (2, 5) and (5, 1) are two opposite vertices of a rectangle. If the other two vertices are points on the straight line \[y = 2x + k\] , then find the value of k.
A. 4
B. 3
C. -4
D. -3

Answer 1

Hints First draw the rectangle with the stated information. Then obtain the mid-point of (2, 5) and (5, 1). The given line passes through the mid-point so, substitute the values of x and y as the obtained mid-point and obtain the value of k.

Formula used
The mid-point of a line with end vertices \[(a,b),(c,d)\] is \[\left( {\dfrac{{a + c}}{2},\dfrac{{b + d}}{2}} \right)\] .

Complete step by step solution
The diagram of the given problem is,

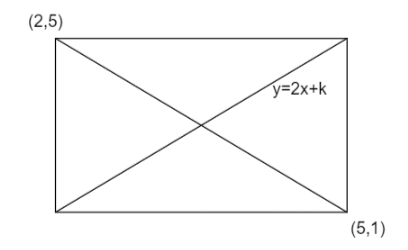
Image: Rectangle
The midpoint of the diagonal with vertices (2, 5) and (5, 1) is
\[\left( {\dfrac{{2 + 5}}{2},\dfrac{{5 + 1}}{2}} \right)\]
\[ = \left( {\dfrac{7}{2},3} \right)\]
From the diagram it is clear that the mid-point is on the given line.
Therefore,
\[3 = 2 \times \dfrac{7}{2} + k\]
\[3 = 7 + k\]
\[k = - 4\]
The correct option is C.

Additional information
The internal angles of a rectangle, which has four sides, are all exactly 90 degrees. At each corner or vertex, the two sides come together at a straight angle. The rectangle differs from a square because its two opposite sides are of equal length.

Note Students sometimes did not understand the fact the given line is the equation of the diagonal line as it is given as -the other two vertices are points of the line \[y = 2x + k\] . But the opposite vertices cannot be the points of a line other than the diagonal, it is clear from the given diagram.