Question

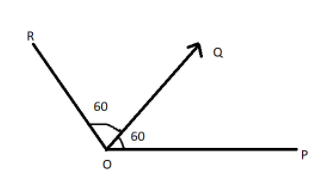
Three coplanar forces each of magnitude $F$ act on a particle at $O$ as shown in the figure. The resultant force is:

A) $2F$ along $OQ$
B) $2F$ along $OP$
C) $\dfrac{{\sqrt 3 }}{2}F$ along $OR$
D) Zero

Answer 1

Hint: Both forces on one plane are coplanar force structures. It can be simultaneous, non-competitive, non-parallel or parallel. The graphical statistics or algebra will solve all these structures. A coplanar force structure is a system of two or more forces whose action lines are crossed by both at one point in particular. However, the universal point may not necessarily be in touch with all the different vectors. These are the simplest powers in which one of several graphic or algebraic alternatives may be solved.

Complete step by step solution:
The single force of the same effect, known as the consequent force or the resulting force, means the arithmetical sum of the different forces for forces that act in the same way and have the same line of operation. If two forces do not have the same action, a method called vector addition of forces may be used to find the magnitude and direction of the resulting force.

There are two visual methods for inserting vectors such as the force triangle and a force parallelogram. The corresponding force is the arithmetic differential of the two powers in the opposite directions along the same line of motion. There are no effects when three or more coplanar forces at a time and the vector diagram closes. The powers at the point of operation are in harmony.

Along vertical, components of $R$ and $Q$ cancel out .But along horizontal, the components of, $OP$ $OQ$ and $OR$ are $F$, $\dfrac {F} {2} $​and $\dfrac {F} {2} $ respectively, which make a total of $2F$ along $OP$.

Note: Coplanar forces mean the forces on an aeroplane. If several forces operate on a person, they are called a power system or a force system. It is regarded as a coplanar force structure in a system where all powers lie on the same plane. This article therefore deals with a system of forces which operate on the same plane and which either share or converge on a similar line of action. If the powers have a similar line of movement, they are known as hills, whereas they are known as concourse when they converge at a common point.

A coplanar or non-coplanar force device can be used. If all forces in a system lie on the same basis, then the coplanar is known as the force system.