Question

Three sides of a square of side \[l\] are occupied by positive charges of density $\lambda {\text{C}}/m$. The net electric field at the centre $O$ is:

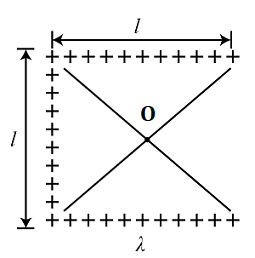
(A) \[\dfrac{{\sqrt 2 {\text{k}}\lambda }}{l}\]
(B) $\dfrac{{2\sqrt 2 {\text{k}}\lambda }}{l}$
(C) $\dfrac{{2{\text{k}}\lambda }}{l}$
(D) $\dfrac{{{\text{k}}\lambda }}{l}$

Answer 1

Hint: Electric Field is the region produced around it by an electric charge whose influence is observed when in that region where the field exists, another charge is brought.
Formula Used: We will use the following formula to find out the solution of this problem:
 \[E = \dfrac{{2\lambda }}{{x\sqrt {{l^2} + 4{x^2}} }}\]
Where
${\text{E}}$ is the net electric field
$\lambda $ is the electric charge density
$l$ is the length of the side of square
 \[x\] is the distance from line charge

Complete Step-by-Step Solution:

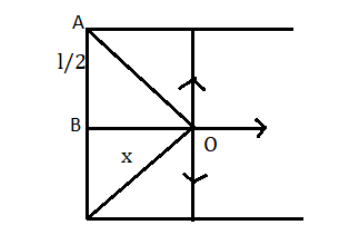
We have been given that the sides of the square are occupied by positive charges of density ${Q_{density}} = \lambda {\text{C}}/m$
The electric fields here are equal and opposite to each other due to the line charge of the top and bottom of the square. They cancel each other, and because of the line on the left side of the square, the net electric field at \[O\] is only the field.
In simpler words, we have
 \[{E_{top}} = {E_{bottom}}\]
The charges on top and bottom are equal magnitude and opposite in polarity.
According to the question and the figure drawn above, we can observe that
 \[x = \dfrac{l}{2}\]
Now we will put the values of \[x\] in the above formula, we get
 \[E = \dfrac{{2\lambda }}{{k\dfrac{l}{2}\sqrt {{l^2} + \dfrac{{4{l^2}}}{4}} }}\]
We can rewrite this equation as
 \[E = k\dfrac{{4\lambda }}{{\sqrt 2 l}}\]
Upon further simplifying, we get
 \[E = \dfrac{{2\sqrt 2 k\lambda }}{l}\]

Therefore, the correct option is (B.)

Note: An electric field surrounds an electric charge and also exerts force at the same time on other charges in the field. It either attracts them or repels them. The electric field is defined mathematically as a vector field that connects the force per unit of charge exerted on an infinitesimal positive test charge to each point in space at that particular point. The volt per meter is the SI unit of electric field strength. Electric field strength is also denoted by Newtons per coulomb. Electric fields are generated by electrical charges, or by magnetic fields that vary in time.