Question

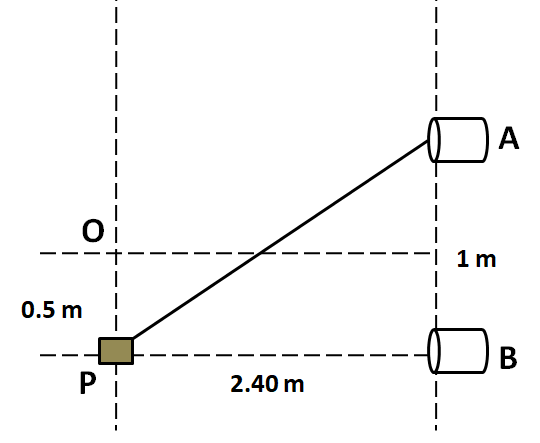
Two speakers A and B are placed $1m$ apart, each produces sound waves of frequency $1800Hz$ in phase. A detector moving parallel to the line joining the speakers at a distance of $2.4m$ away detects a maximum intensity at O and then at P. Speed of the sound wave is:

(A) $330m{s^{ - 1}}$
(B) $360m{s^{ - 1}}$
(C) $350m{s^{ - 1}}$
(D) $340m{s^{ - 1}}$

Answer 1

Hint: To solve this question, we have to find out the path difference at the two points O and P. Then applying the conditions of the maxima at these points, we can get the wavelength of the sound. The frequency is already given in the question, and from the relation between the frequency and the wavelength, the velocity of the sound wave can be found out.
Formula used: The formula used to solve this question is given by
$\lambda = \dfrac{v}{f}$, here $\lambda $ is the wavelength, $v$ is the velocity, and $f$ is the frequency of a wave.

Complete step-by-step answer:
Let the speed of the sound wave be $v$.
The frequency of the sound wave produces by each of the sources is given to be $1800Hz$, that is,
$f = 1800Hz$
We know that the wavelength is given by
$\lambda = \dfrac{v}{f}$
So the wavelength of the sound produced by each source is
$\lambda = \dfrac{v}{{1800}}$ ……………...(1)
Now, let us label the midpoint of the line AB joining the two sources as C, which is shown in the below figure.

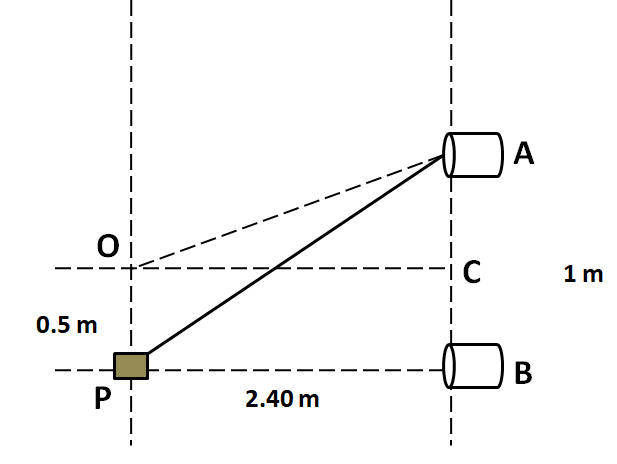
In the triangle AOC, by the Pythagoras theorem we get
$O{C^2} + A{C^2} = O{A^2}$
$ \Rightarrow {2.4^2} + {0.5^2} = O{A^2}$
On solving we get
$OA = 2.45m$
Similarly, we have $OB = 2.45m$
The path difference at O is
$PD = OA - OB$
$PD = 2.6 - 2.6 = 0$
So the path difference at O is equal to zero.
Hence, there will be central maxima at O.
According to the question, the next maxima occurs at P. Therefore, there occurs the first maxima at P.
So the path difference at P must be
$PD' = 1\lambda = \lambda $ ………………..(2)
In the triangle APB, applying Pythagoras theorem
$A{B^2} + B{P^2} = A{P^2}$
From the above figure, $BP = 2.4m$ and $AB = 1m$. Substituting these above we get
${1^2} + {2.4^2} = A{P^2}$
On solving we get
$AP = 2.6m$
Also, from the above figure, we have $BP = 2.4m$.
So the path difference at P is given by
$PD' = AP - BP$
$ \Rightarrow PD' = 2.6 - 2.4$
On solving
$PD' = 0.2m$ ………………….(3)
From (2) and (3)
$\lambda = 0.2m$
From (1)
$\dfrac{v}{{1800}} = 0.2$
$ \Rightarrow v = 360m{s^{ - 1}}$
Thus, the velocity of the sound wave is equal to $360m{s^{ - 1}}$.

Hence, the correct answer is option B.

Note: We should not get confused in the indexing of the maximas. Although the central maxima is encountered first, then also the maxima next to the central maxima will be called the first.