NCERT Solutions for Class 4 Maths Chapter Patterns

Patterns are everywhere, from the stripes on a tiger to the tiles on your kitchen floor. Teaching children to recognize and understand patterns is like giving them a key to unlock the world of numbers, logic, and creativity.

If you're a parent looking to simplify Class 4 Maths for your child, this blog on patterns from the NCERT curriculum is just what you need. Let’s dive into the magic of patterns and how they play a crucial role in mathematical learning.

Introduction to Patterns in Class 4 Maths

Patterns are the heartbeat of mathematics, weaving logic into everyday life. For children in Class 4 Maths, understanding patterns is like solving a delightful puzzle that combines observation, prediction, and creativity. Let’s explore why studying patterns is vital and how they apply to the world around us.

Importance of Studying Patterns

Patterns are more than just fun—they are fundamental to developing problem-solving and analytical skills. Recognizing patterns helps children with the following:

• Improve Logical Thinking: Identifying sequences sharpens the ability to predict outcomes.

• Build Problem-Solving Skills: Patterns provide a foundation for tackling advanced math concepts like algebra and geometry.

• Enhance Observation Skills: Children learn to notice details, improving their ability to analyze and interpret information.

By studying patterns, children gain essential skills that benefit their academic and everyday lives.

Application of Patterns in Daily Life

Patterns aren’t limited to textbooks—they’re everywhere around us! Helping children spot patterns in their surroundings makes learning more relatable and exciting.

Examples of patterns in daily life include the following:

• Nature: Stripes on a zebra, spirals in a sunflower, or the branching of trees.

• Designs: Rangoli, Mehndi, and floor tiles.

• Routine: Traffic lights, days of the week, or school schedules.

Encourage your child to spot patterns around them—it’s a game that turns everyday moments into learning opportunities!

Connecting patterns to daily life fosters curiosity and creativity in children, making math both practical and fun.

Overview of the Types of Patterns Covered in the Chapter

This chapter introduces children to different types of patterns, including the following:

• Repeating Patterns: Sequences that repeat predictably (e.g., red, blue, red, blue).

• Growing Patterns: Patterns that evolve step-by-step (e.g., 1, 2, 3, 4).

• Symmetrical Patterns: Designs that mirror each other (e.g., butterfly wings).

• Number Patterns: Rules that connect numbers in sequences (e.g., adding 2 each time).

By learning these patterns, children build a solid foundation for understanding advanced math concepts.

Let’s dive deeper into each type, starting with repeating patterns!

Understanding Repeating Patterns

Repeating patterns are like a catchy chorus in a song—they repeat themselves and make things predictable and fun! These patterns are a great way for children to understand sequences and develop problem-solving skills. Let’s explore what repeating patterns are and how they appear all around us.

Definition and Characteristics of Repeating Patterns

Repeating patterns are sequences where a specific set of elements occurs again and again in the same order. These patterns can involve colors, shapes, numbers, or even sounds.

Key Characteristics:

• Predictability: The sequence repeats without any change.

• Fixed Units: The repeating part of the pattern is called the core.

• Simplicity: They are easy to observe and follow, making them perfect for beginners.

Example:

• Core Unit: Red, Blue

• Pattern: Red, Blue, Red, Blue, Red, Blue…

Understanding the definition and structure of repeating patterns lays the groundwork for recognizing them in various forms.

Examples of Repeating Patterns in Nature and Objects

Repeating patterns are everywhere, from the natural world to man-made objects. Encourage your child to spot them in everyday life to make learning interactive and exciting.

Examples:

• Nature:

• Zebra stripes

• Honeycomb hexagons

• Alternating petals on flowers

• Objects:

• Bead necklaces

• Rangoli designs

• Wallpaper patterns

Examples from the real world make patterns relatable and help kids see math in action.

How to Identify Repeating Patterns in Sequences

Spotting a repeating pattern is easy when you know what to look for.

Here’s how you can guide your child to spot a pattern:

• Find the Core Unit: Identify the smallest set of elements that repeats.

• Observe Continuity: Check if the same order recurs.

• Predict the Next Element: Use the core unit to guess what comes next.

Example:

• Sequence: ●▲●▲●▲

• Core unit: ●▲

• Next in the pattern: ●▲

Identifying repeating patterns teaches children to observe, analyze, and predict, building essential cognitive skills.

Want to help your child master Play with Patterns in Class 4 Maths? Download the detailed revision notes now and give them the tools to excel in their exams!

Ready to move on? Let’s explore the fascinating world of growing patterns next!

Developing Growing Patterns

Just like plants grow taller and wider over time, growing patterns expand or evolve step by step. These patterns are a fantastic way to help children understand the concept of change and progression. Let’s dive into what growing patterns are, how they differ from repeating patterns, and some simple exercises to help your child identify them.

Explanation of Growing Patterns

A growing pattern is a sequence in which each step builds upon the previous one. As the pattern progresses, the elements increase or expand in a specific, predictable way. This could involve adding more items, increasing numbers, or expanding shapes.

For Example:

• 1, 2, 3, 4, 5...

• The number of blocks: 1, 2, 3, 4, 5…

Key Characteristics:

• The pattern grows progressively.

• Each new step is larger or more complex than the one before.

• The rate of growth is usually constant (e.g., adding 1 each time, adding 2 each time).

Growing patterns help children visualize progression, which is an important skill in both math and real-world situations.

Differences Between Growing and Repeating Patterns

Though both types of patterns are predictable, they have the following key differences:

• Repeating Patterns: The sequence stays the same throughout. The same set of elements is repeated again and again.

• Example: Red, Blue, Red, Blue, Red, Blue...

• Growing Patterns: The sequence changes as it moves forward. Each step adds something new or increases in some way.

• Example: 1, 2, 3, 4, 5…

While repeating patterns stay constant, growing patterns develop and evolve, helping children understand change and continuity.

Simple Exercises to Identify Growing Patterns

Here are a few easy exercises to help your child identify and create growing patterns:

1. Counting Stars: Start with 1 star. Then add 2 stars, 3 stars, and so on.

• Sequence: ★, ★★, ★★★, ★★★★

2. Building with Blocks: Start with 1 block, then add 2, then 3, etc.

• Sequence: 1, 3, 6, 10...

Simple exercises help children understand how things evolve and grow, fostering creativity and analytical thinking.

Understanding number patterns is essential for building a strong foundation in maths. Check out Vedantu's interactive lessons on Number Patterns to help your child grasp key concepts and boost their problem-solving skills!

Ready for more? Next, we’ll explore symmetrical patterns, where everything mirrors itself!

Exploring Symmetrical Patterns

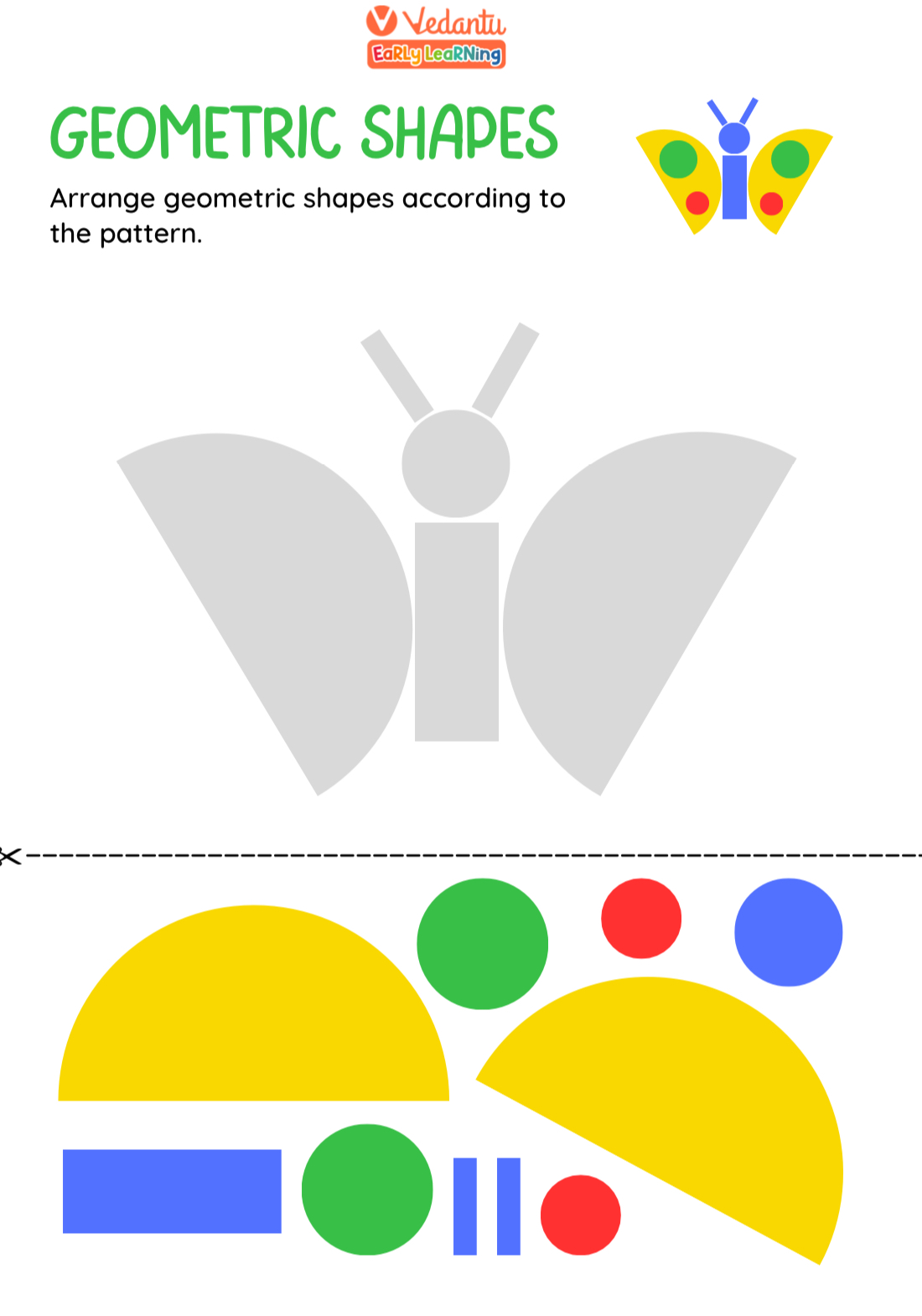
Symmetry is everywhere! From the natural world to everyday objects, symmetrical patterns create balance and harmony. Understanding symmetry not only makes math fun but also helps children see the beauty in the world around them. Let’s explore the magic of symmetrical patterns and how to recognize and create them!

Introduction to Symmetry in Patterns

Symmetry refers to a balanced arrangement where one half of a shape or design mirrors the other. When something is symmetrical, one side is a reflection or duplication of the other. In math, symmetry helps children understand balance, reflection, and how shapes interact with each other.

Key Characteristics:

• Mirrored Design: Both sides are identical when split down the middle.

• Line of Symmetry: The line that divides the shape into two equal parts.

Symmetry introduces children to the idea of balance and equality, both in math and in life.

Visual Recognition of Symmetrical Patterns

Recognizing symmetrical patterns can be quite fun once you know what to look for! These patterns often appear in nature and art, where one side mirrors the other.

Examples of Symmetry:

• Butterfly Wings: The left and right wings of a butterfly are mirror images.

• Human Face: The left side of the face is almost a mirror image of the right.

• Flower Petals: Many flowers, like daisies, have symmetrical petals arranged around a central point.

How to Spot Symmetry:

• Look for equal halves: Identify if the shape or pattern can be split into two identical parts.

• Use a mirror: Hold a mirror along a line and see if both sides match.

Visual recognition of symmetry in everyday objects makes it easier for children to identify symmetrical patterns and appreciate the concept.

Practical Activities to Create Symmetrical Designs

Here are some hands-on activities that will help your child create symmetrical designs:

1. Folded Paper Art:

• Take a square piece of paper, fold it in half, and use crayons or paint on one side. After opening the paper, children will see a symmetrical design formed from the folded side.

2. Mirror Drawing:

• Draw half of a shape or figure on a piece of paper and ask your child to complete the other half using symmetry. Use a mirror to help them see the reflection.

3. Symmetrical Nature Walk:

• Go on a walk with your child and spot symmetrical patterns in nature. Look for things like leaves, flowers, and animal markings that show symmetry.

Practical activities help children grasp symmetry in a hands-on, engaging way.

Want clear and structured solutions for your child’s Class 4 Maths chapter? Explore Vedantu's detailed NCERT Solutions and give your child the perfect guidance for tackling each problem!

Now that we’ve explored symmetry, let’s move to the next exciting type of pattern—number patterns!

Number Patterns and Sequences

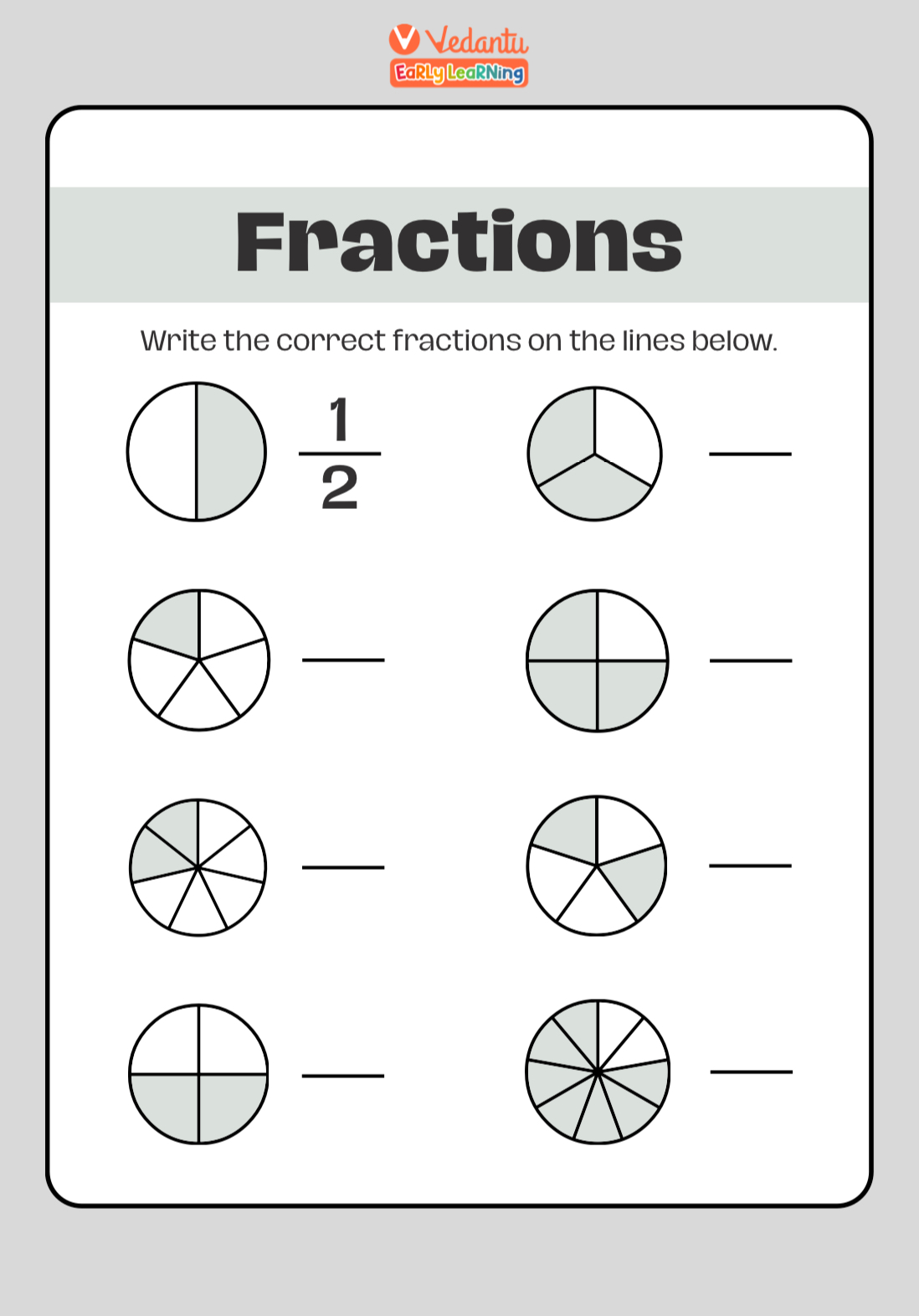
Number patterns and sequences are like puzzles where numbers follow specific rules. They’re an essential part of Class 4 Maths that help children understand order, structure, and predictability. Let's dive into the world of number patterns, how to identify them, and how to predict what comes next!

Introduction to Number Patterns

Number patterns are simply sequences of numbers that follow a particular rule or pattern. Recognizing these patterns helps children build a strong foundation in mathematical thinking. Whether it’s counting, adding, or multiplying, number patterns are everywhere!

Key Characteristics:

• Consistency: Numbers in the pattern follow a specific rule.

• Predictability: Once the rule is identified, it's easy to predict the next number.

Example:

• 2, 4, 6, 8, 10, … (The pattern increases by 2 each time.)

Number patterns form the building blocks for more complex math concepts.

Identifying Arithmetic Sequences

An arithmetic sequence is a special kind of number pattern where each number is obtained by adding a constant number to the previous one. This "constant difference" makes it easy to predict future numbers.

How to Identify Arithmetic Sequences:

• Look for a consistent difference between each number in the sequence.

• This difference is called the common difference.

Example of Arithmetic Sequence:

• 5, 10, 15, 20, 25, … (The common difference is 5.)

Understanding arithmetic sequences is a key skill in mastering number patterns.

Techniques to Predict the Continuation of Number Patterns

Once children understand the rule of a number pattern, predicting the next number becomes easy! Here are some simple techniques to help children predict the continuation of number patterns:

1. Look for the Common Difference: In arithmetic sequences, subtract one number from the next to find the common difference. Then, add that difference to the last number to predict the next one.

2. Check for Addition or Subtraction: Some patterns might involve adding or subtracting numbers to continue the sequence.

3. Visualize the Pattern: Drawing or writing out the sequence can help children visualize how the numbers change.

Example:

• Sequence: 2, 4, 6, 8, …

• Common difference: +2

• Next number: 8 + 2 = 10

With a little practice, predicting the continuation of number patterns becomes an easy and fun task.

Now that we’ve covered number patterns, let's move on to using patterns to solve problems!

Using Patterns to Solve Problems

When children learn to recognize patterns, they develop a deeper understanding of how numbers and shapes work together, helping them solve problems more efficiently. Let’s explore how patterns can aid problem-solving and look at some examples of pattern-based math problems.

How Patterns Can Aid Problem-Solving

Patterns are helpful in problem-solving because they allow us to predict what comes next. Once we recognize a pattern, we can apply that knowledge to solve similar problems quickly and accurately. Patterns help us with the following:

• Simplify Complex Problems: Instead of looking at each step individually, patterns let us see the bigger picture.

• Identify Missing Elements: When a number or shape is missing, recognizing the pattern can help fill in the blanks.

• Make Predictions: Patterns help children predict the next step or number, saving time and effort in problem-solving.

Recognizing patterns gives kids a "toolbox" to tackle mathematical challenges, making problem-solving much easier.

Examples of Pattern-Based Problem-Solving in Maths

By recognizing the repeating or growing patterns, children can easily predict and solve problems without having to start from scratch each time.

1. Arithmetic Sequences: If the sequence is 3, 6, 9, 12, what is the next number?

• Solution: The pattern increases by 3, so the next number is 15.

2. Shape Patterns: In a pattern of triangles (△, △, □, △, △, □…), what comes after the last square?

• Solution: The pattern repeats every 3 shapes, so the next shape is a triangle (△).

Now, let’s move on to some practice problems to help your child sharpen their pattern-recognition skills!

Practice Problems Involving Pattern Recognition

Here are five fun practice problems to help your child master pattern recognition:

1. Number Pattern: 5, 10, 15, 20, __? (What comes next?)

2. Shape Pattern: ○, □, ○, □, __? (What comes next?)

3. Number Pattern: 2, 4, 8, 16, __? (What comes next?)

4. Number Pattern: 1, 3, 5, 7, __? (What comes next?)

5. Color Pattern: Red, Blue, Red, Blue, __? (What comes next?)

These practice problems help children recognize different types of patterns and apply their problem-solving skills. Keep practicing, and soon your child will be a pattern-solving pro! 

Help your child revise effectively with Vedantu's easy-to-understand revision notes. These notes break down all the key concepts of the Play with Patterns chapter, ensuring thorough preparation.

Next, we’ll explore how patterns can also spark creativity in learning!

Patterns and Creativity

Patterns are not only helpful in math but also spark creativity. When children understand how patterns work, they unlock the potential to think outside the box, create their designs, and express their imagination. Let's dive into the link between patterns and creative thinking, and how you can encourage your child to use patterns in fun and exciting ways.

Link Between Patterns and Creative Thinking

Understanding and creating patterns allows children to think creatively. When kids recognize repetitive structures and relationships, they begin to connect ideas in new ways. Patterns encourage children to do the following:

• Imagination: Seeing patterns in objects, numbers, or shapes lets children experiment with designs and ideas.

• Innovation: Patterns allow kids to explore different combinations, leading to unique creations.

• Problem-Solving: Understanding how patterns work helps children approach problems with innovative solutions.

Patterns are not just about numbers and shapes—they help children tap into their creativity and develop innovative thinking skills.

Encouraging Students to Create Their Patterns

When children create their patterns, they become the "artists" of their math world! Here’s how to inspire your child to design their patterns:

• Use Everyday Objects: Ask children to create patterns using beads, buttons, or colored blocks.

• Explore Number Patterns: Encourage kids to make their number sequences, experimenting with addition or subtraction.

• Mix and Match Shapes: Let children create patterns with different shapes and colors, such as triangles, squares, and circles.

Creating their patterns boosts children’s confidence and helps them understand the underlying principles of structure and design.

Utilizing Patterns in Art and Design in Classroom Projects

Patterns are a fantastic way to make art projects more exciting. Incorporating patterns into classroom activities makes learning enjoyable and allows children to see how math connects to creativity. Here are some ways to use patterns in art projects:

• Rangoli Designs: Use colors and shapes to create beautiful, symmetrical patterns.

• Tessellation Art: Create repeating shapes that fit together perfectly, like tiles on a floor.

• Patterned Mosaics: Use colored paper or stones to create intricate patterns in a design.

Using patterns in art not only makes projects fun but also reinforces the importance of structure in creative work. 

Take your child’s math skills to the next level with Vedantu's SuperMaths. These engaging lessons are designed to make learning math fun and rewarding. Book a free demo session today!

With these activities, your child can combine math and art in ways that are both educational and exciting.

Conclusion

In this blog on Patterns, we’ve explored repeating, growing, symmetrical, and number patterns from class 4 maths. Understanding these concepts helps children build strong problem-solving and logical thinking skills, essential for future mathematical concepts like algebra, geometry, and even higher-level problem-solving.

Mastering patterns also nurtures creativity and observation skills, which are valuable both inside and outside the classroom. To further your child’s learning and mastery of patterns, Vedantu offers interactive lessons designed to make math fun and engaging.

Book a free demo session today and help your child develop a strong foundation in mathematics!