Maharashtra Board Class 12 Solutions for Chemistry Chapter 1 Solid State - PDF

Exercises

1. Choose the most correct option.

i. Molecular solids are

1. crystalline solids

2. amorphous solids

3. ionic solids

4. metallic solids

Ans: The correct option is a. Crystalline solids.

Crystalline solids are arranged in a specific order, whereas molecular solids are composed of various molecules and are also arranged in a specific order. Molecular Solids are therefore Crystalline Solids.

ii. Which of the following is n-type semiconductor?

1. Pure Si

2. Si doped with As

3. Si doped with Ga

4. Ge doped with In

Ans: The correct option is b. Si doped with As. 

Si belongs to group 14 while As is in group 15 of elements. One more electron is present when As is added to Si, creating an n-type semiconductor.

iii. In Frenkel defect

1. Eectrical neutrality of the substance is changed.

2. Density of the substance is changed.

3. Both cation and anion are missing

4. Overall electrical neutrality is preserved

Ans: The correct option is d. overall electrical neutrality is preserved. 

Overall neutrality is maintained because an equal amount of cations and anions are absent from their positions.

iv. In crystal lattice formed by bcc unit cell the void volume is

1. 68%

2. 74%

3. 32%

4. 26%

Ans: The correct option is c. 32%. 

The total volume-occupied volume is the same as the Void volume. Out of the hundred percent total volume, 32% of the volume is void, while 68% of the volume is occupied.

v. The coordination number of atoms in bcc crystal lattice is

1. 2

2. 4

3. 6

4. 8

Ans: The correct option is d. 8. 

The number of atoms encircling a core atom is known as the coordination number. CsCl is an illustration of bcc, as an example. 8Cl- is located at Cs+.

vi. Which of the following is not correct?

1. Four spheres are involved in the formation of tetrahedral void.

2. The centres of spheres in octahedral voids are at the apices of a regular tetrahedron.

3. If the number of atoms is N the number of octahedral voids is 2N.

4. If the number of atoms is N/2, the number of tetrahedral voids is N.

Ans: The correct option is c. If the number of atoms is N the number of octahedral voids is 2N.

In a lattice, the number of atoms is always equal to the number of octahedral voids. Thus, if N atoms exist, then the void will also be N.

vii. A compound forms the hcp structure. Number of octahedral and tetrahedral voids in 0.5 mole of substance is respectively

1. 3.011 × 10²³, 6.022 × 10²³

2. 6.022 × 10²³, 3.011 × 10²³

3. 4.011 × 10²³, 2.011 × 10²³

4. 6.011 × 10²³, 12.022 × 10²³

Ans: The correct option is a. 3.011 × 10²³, 6.022 × 10²³.

There are three levels of atoms in the hcp structure. Six atoms form a hexagonal arrangement in the top and bottom layers, while a seventh atom sits in the centre of the hexagonal arrangement. Three atoms in the intermediate layer are tucked away in the top and bottom plane's triangular grooves.

viii. Pb has fcc structure with edge length of unit cell 495 pm. Radius of Pb atom is

1. 205 pm

2. 185 pm

3. 260 pm

4. 175 pm

Ans: The correct option is d. 175 pm.

Atoms can be found in an FCC unit cell at the cube's centre and on each of the crystal lattice's four corners. Only half of each atom, which is located at the face centre, is assigned to one particular cell; the other half is shared by two adjacent unit cells.

2. Answer the following in one or two sentences.

(i) What are the types of particles in each of the four main classes of crystalline solids?

Ans: Atoms, ions, and molecules are the tiniest constituents or particles of various materials.

(ii) Which of the three types of packing used by metals makes the most efficient use of space and which makes the least efficient use?

Ans: The most effective particle packing is found in fcc, while the least effective packing is seen in scc.

(iii) The following pictures show population of bands for materials having different electrical properties. Classify them as insulator, semiconductor or a metal.

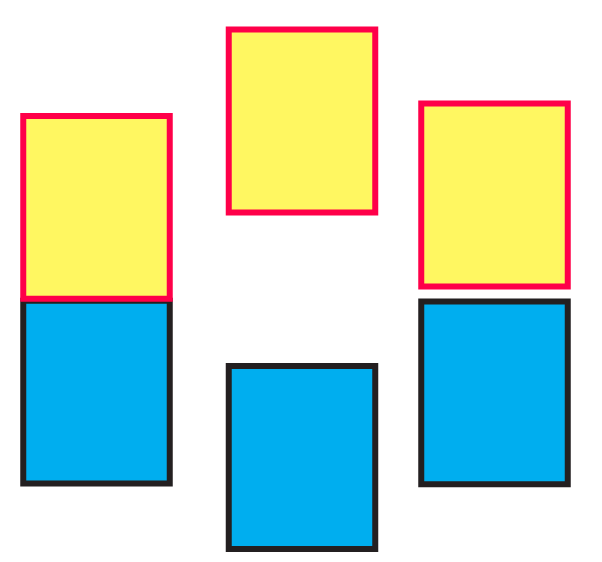
Ans: Pictures A, B, and C show a metal conductor, an insulator, and a semiconductor, respectively.

(iv) What is a unit cell?

Ans: The smallest recurring structural unit that contributes to the formation of a crystalline solid or crystal lattice is known as a unit cell. All the qualities of a crystalline solid are present in the unit cell.

(v) How does electrical conductivity of a semiconductor change with temperature? Why?

Ans: The electrons from the valence band in semiconductors can be promoted to the conduction band by heating because the energy difference between the valence band and conduction band is not great. As a result, a semiconductor's electrical conductivity increases with temperature.

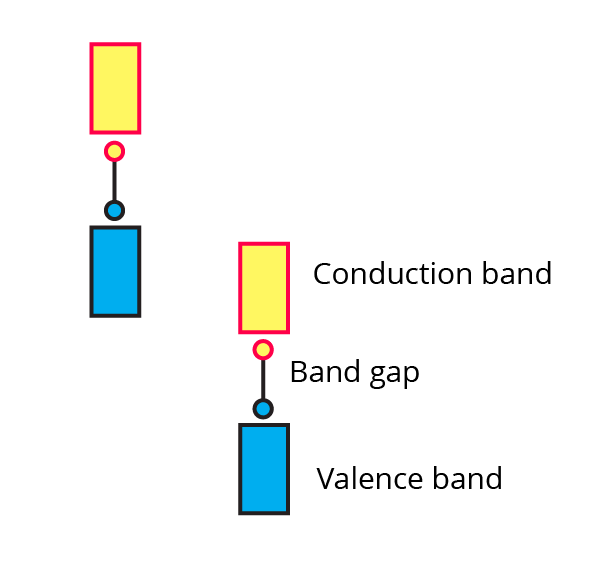
(vi) The picture represents bands of MOs for Si. Label valence band, conduction band and band gap.

Ans:

(vii) A solid is hard, brittle and electrically non-conductor. Its melt conducts electricity. What type of solid is it?

Ans: NaCl is an example of a solid crystalline electrolyte that is brittle, rigid, and electrically nonconducting. But its melt is electrically conductive.

(viii) Mention two properties that are common to both hep and ccp lattices.

Ans: Crystal lattices in hcp and ccp have a coordination number of 12 and a packing efficiency of seventy-four percent.

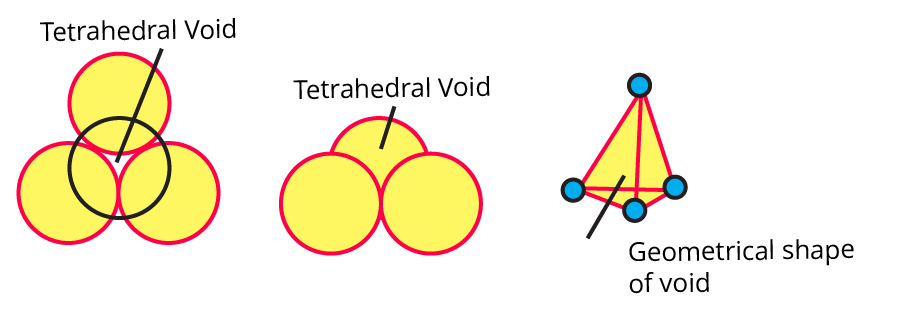
(ix) Sketch a tetrahedral void.

Ans:

(x) What are ferromagnetic substances?

Ans: The term "ferromagnetic" refers to materials that have unpaired electrons, have a high paramagnetic character, are strongly attracted by magnetic fields when placed in them, and nevertheless exhibit persistent magnetic moments even when the external magnetic field is withdrawn. They are able to be magnetised permanently.

3. Answer the following in brief.

(i) What are valence band and conduction band?

Ans: There are no free mobile electrons in valence bands because they are involved in bonding, which fills the atomic orbitals with electrons from the inner shells.

Conduction bands, where electrons are delocalized and can carry heat and electricity, are formed by atomic orbitals that are partially full or empty and overlap.

(ii) Distinguish between ionic solids and molecular solids.

Ans: The following table shows the differences between the ionic and molecular solids.

(iii) Calculate the number of atoms in a fcc unit cell.

Ans: The face-centred cubic unit cell is provided.

How many atoms are there in the corner?

\dfrac{1}{8}\times8=1

Making an estimate of the atoms in the faces:

\dfrac{1}{2}\times6=3

Counting the total number of atoms:

3 + 1 = 4

There are four atoms overall in the face-centred cubic unit cell.

(iv) How are the spheres arranged in the first layer of simple cubic close-packed structures? How are the successive layers of spheres placed above this layer?

Ans: Each layer of spheres in a simple cubic closed-packed construction fills in any gaps left by the layer before it. At their intersection, three adjacent spheres in the first layer will create a hollow area.

One layer's particles line up to fit into the hollow spaces left by the previous layer. Directly above the first layer is the third layer.

(v) Calculate the packing efficiency of a metal crystal that has a simple cubic structure.

Ans: Since each simple cubic unit cell contains one atom. The following formula can be used to determine how efficiently a simple cubic unit cell is packed.

Packing efficiency =$ \dfrac{4\pi\ r^{3}}{(2r^{2})^{3}}\times100$

                                = $\dfrac{1}{6}\pi\times100$

                                = 52.4

The packing efficiency is fifty-two point four percent.

(vi) What are paramagnetic substances? Give examples.

Ans: The atoms or molecules that exhibit a weak magnetic field attraction are known as paramagnetic substances. Single electrons in these compounds all spin in the same direction. For instance: transition metal complexes, oxygen, iron oxide, aluminium, and so on.

(vii) What are the consequences of Schottky defect?

Ans: When an equal number of cations and anions leave the crystal lattice, vacancies are created, resulting in a Schottky defect, a type of point defect. The density of the crystal is decreased when there are several Schottky defects present.

(viii) Cesium chloride crystallises in a cubic unit cell with Cl– ions at the corners and Cs+ ions in the centre of the cube. How many CsCl molecules are there in the unit cell ?

Ans: BCC (body-centred crystalline) describes the structure of CsCl.

So, a cubic cell has the following number of atoms:

$=4\times\dfrac{1}{4}+1\times1$

= 2

In the CsCl crystal, each unit cell has 2 atoms.

(ix) Cu crystallizes in fee unit cell with edge length of 495 pm. What is the radius of Cu atom ?

Ans: The given data: a = 495 pm

To find: Radius (r)

Formula:

$r=\dfrac{a}{2\sqrt{2}}$

Calculation:

$r=\dfrac{495}{2\sqrt{2}} $

r = 175 pm

Therefore, the radius of the Cu atom is 175 pm.

(x) Obtain the relationship between density of a substance and the edge length of unit cell.

Ans: Think about a cubic unit cell with an edge length of a.

• Unit cell volume is equal to a3.

• If each unit cell contains "n" particles and each particle have "m" mass, then unit cell mass is equal to m x n.

• If the substance's unit cell density is ρ, then

$\text{Density of unit cell}=\dfrac{\text{mass of unit cell}}{\text{Volume of unit cell}}\rho=\dfrac{m\times n}{a^{3}}$

4. The density of iridium is 22.4 g/cm3. The unit cell of iridium is fcc. Calculate the radius of iridium atom. Molar mass of iridium is 192.2 g/mol.

Ans: The given data:

Density is 22.4 g/cm3

Molar mass is 192.2 g/mol

Calculating density:

$\rho=\dfrac{z M}{a^3 N_a}\\ a=2 \sqrt{2} \times r\\ \rho=\dfrac{z M}{(2 \sqrt{2} \times r)^3 N_a}$

Rearranging the equation and calculating for the radius:

Therefore, the radius of the iridium atom is 1.36 x 10-10 m [or] 136 pm.

5. Aluminium crystallises in a cubic close packed structure with unit cell edge length of 353.6 pm. What is the radius of an Al atom ? How many unit cells are there in 1.00 cm3 of Al ?

Ans: The given data:

a = 353.6 x 10-10 cm

Volume = 1 cm3

Formula used:

$a=2\sqrt{2}\times r$

Calculating the radius:

$r=\dfrac{a}{2 \sqrt{2}}\\

Calculating the volume of the unit cell:

$a=353.6\times10^{-10}cm\\ a^{3}=44.21\times10^{-24}cm^{3}$

Calculating the number of unit cell:

Number of unit cell 

$=\dfrac{1}{44.21}\times10^{-24}\\$

$=2.262\times10^{-22}$

6. In an ionic crystalline solid atoms of element Y form hcp lattice. The atoms of element X occupy one third of tetrahedral voids. What is the formula of the compound?

Ans: Given data:

The number of atoms in the given hcp lattice (Y) is 6.

The number of tetrahedral voids (2 x 6) is 12.

⅓ of the voids are occupied by X.

$12\times\dfrac{1}{3}=4$

The value of X is 4. Hence, the compound formula would be X2Y3.

7. How are tetrahedral and octahedral voids formed?

Ans: Tetrahedral voids, which appear in cubic close packing structures when four particles align themselves to fill the space between one another, are most common in ABAB tight packing.

Octahedral voids are created in ABCABC tight packing when six particles align, leaving a space between them. Tetrahedral and octahedral voids are produced by four and six particles, respectively.

8. Third layer of spheres is added to the second layer so as to form hcp or ccp structure. What is the difference between the addition of a third layer to form these hexagonal close-packed structures?

Ans: Cubic close packing's third layer is crucial since it determines whether the pattern will be ABCABC or ABABAB.

For instance,

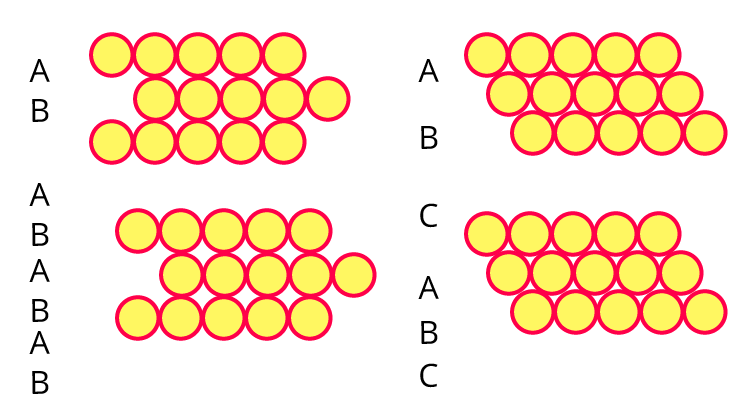
The density, quantity, and type of voids that are created inside their layer can all be impacted by the layer's alignment.

9. An element with molar mass 27 g/mol forms a cubic unit cell with an edge length of 405 pm. If the density of the element is 2.7 g/cm3, what is the nature of a cubic unit cell? (fcc or ccp)

Ans: The given data:

Molar mass is 27 g/mol [or] 0.02 kg/mol.

Edge length (a) is 4.05 x 10-10 m

Density is 2.7 g/cm3 [or] 2.7 x 103 kg/m3.

The formula used:

$r=\dfrac{a}{2 \sqrt{2}}\\

Calculation:

$n=\dfrac{2.7 \times 10^3 \times\left(4.05 \times 10^{-10}\right)^3 \times 6.022 \times 10^{23}}{0.027}\\$

n=4

Therefore, the structure of the crystal is FCC.

10. An element has a bcc structure with unit cell edge length of 288 pm. How many unit cells and number of atoms are present in 200 g of the element? (1.16 × 1024, 2.32 × 1024)

Ans: Calculating the volume of the element:

$\text { Volume of the element }=\dfrac{\text { Mass }}{\text { Density }}\\ =\dfrac{208}{7.2}\\$

=28.89

Calculating the number of unit cells:

$\text { Number of unit cells }=\dfrac{\text { Total Volume }}{\mathrm{} \text { Volume of a unit cell }}\\$

$=\dfrac{28.89}{2.389 \times 10^{-23}}\\$

$=12.09 \times 10^{23}$

The number of atoms present in the BCC lattice is 2.

The number of atoms present in 208 g is equal to the number of atoms per unit cell multiplied by the number of unit cells present.

$=2\times12.09\times10^{23}\\ =24.18\times10^{23}\\ =2.418\times10^{24}\\$

Therefore, the number of atoms present in 208 g is 2.418 x 1024.

11. Distinguish with the help of diagrams metal conductors, insulators and semiconductors from each other.

Ans: The following table shows the differences between the metal conductors, insulators, and semiconductors.

Conductors	Insulators	Semiconductors
A conductor is a material that more effectively carries heat and electricity.	Insulators are substances that, under any circumstances, cannot conduct heat or electricity.	A semiconductor is a substance that conducts electricity poorly at low temperatures but better at higher ones.
Metals and Alloys are good examples of a conductor.	Wood, rubber, and plastic are good examples of insulators.	Germanium and Silicon are good examples of semiconductors.

12. What are n-type semiconductors? Why is the conductivity of doped n-type semiconductor higher than that of pure semiconductor? Explain with diagram.

Ans: When a lower group element is doped with higher group elements, n-type semiconductors are produced. For instance, Si is doped with As, resulting in the presence of free electrons.

A group of 15 elements adds one extra electron to each atom in a semiconductor, increasing the number of species (electrons) available to carry current compared to a pure semiconductor. Additional conductivity results from the presence of more electrons.

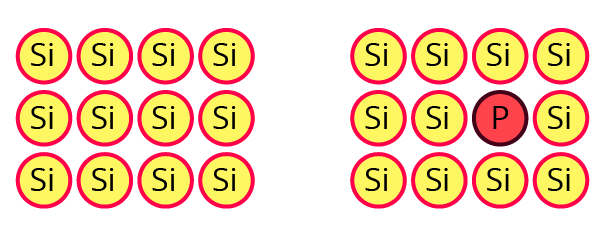
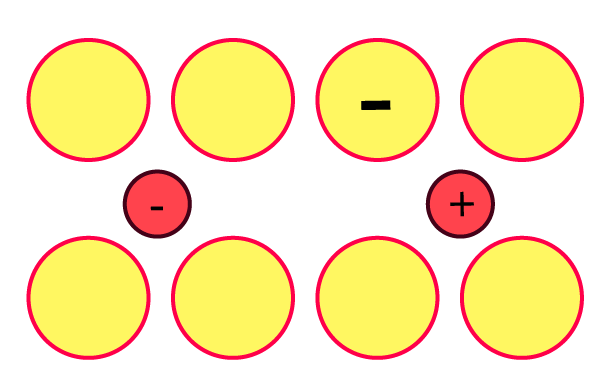
13. Explain with a diagram. Frenkel defect. What are the conditions for its formation? What is its effect on density and electrical neutrality of the crystal?

Ans: When cations are present in interstitial space rather than their usual location in the lattice structure, a Frenkel defect occurs.

When cations are smaller than anions and have a big interstitial gap, this occurs. where the cation fits. A low coordination number is an additional requirement. Due to no ions escaping the lattice, electrical neutrality and density are unaffected.

14. What is an impurity defect? What are its types? Explain the formation of vacancies through aliovalent impurity with example.

Ans: When there are foreign atoms present in the interstitial or lattice location in place of host atoms. These come in two varieties.

When SrCl2 is added to ionic solids like sodium chloride, vacancies are produced as a result. Covalent solids, such as Si doped with As or In, are an example. There are holes or extra electrons in this. P-type and n-type are the further separated divisions.

An electron is lost when a lower group element, such as In, is introduced to silicon, creating a hole or vacancy. P-type semiconductors are referred to as such because they form positive charges.

Can You Recall? 

1. What are the three most common states of matter?

Ans: Matter exists in three different states. The three are liquid, solid, and gas. By examining the configuration of their particles, it is possible to understand why they have various qualities.

2. How does solid-state differ from the other two states? (Answer with reference to volume, shape, effect of temperature and pressure on these and the motion of constituent particles and interparticle forces.)

Ans: Things that exist in the solid state are composed of densely packed particles with small spaces between them. Solids cannot be crushed, have a fixed shape and volume, and have little kinetic energy. These are the characteristics to consider when contrasting solids with liquid and gaseous phases.

Try this. (Textbook Page No. 1)

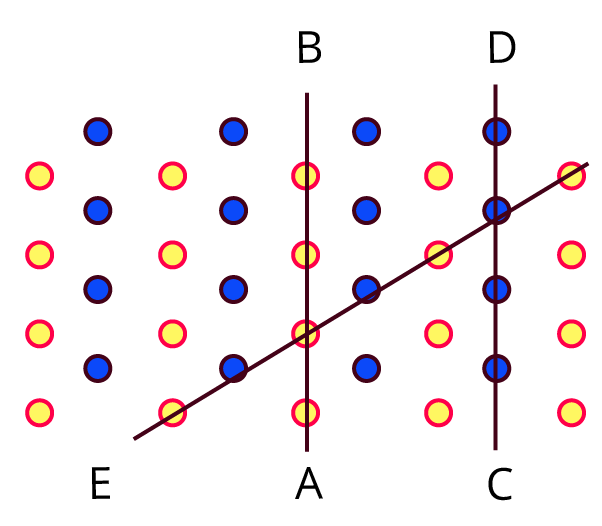
Observe the above figure carefully. The two types of circles in this figure represent two types of constituent particles of a solid.

• Will you call the arrangement of particles in this solid regular or irregular?

Ans: This solid's particle arrangement is called regular.

• Is the arrangement of constituent particles in directions $\overline{AB}, \overline{CD} and \overline{EF}$ same or different?

Ans: $\overline{AB}$ depicts a configuration of identical particles of a single type.

$\overline{CD}$ is a configuration of identical particles of a different type.

$\overline{EF}$ shows a consistent placement of two distinct particles in contrasting places.

Use Your Brain Power! (Textbook Page No. 2)

Identify the arrangements A and B as crystalline or amorphous.

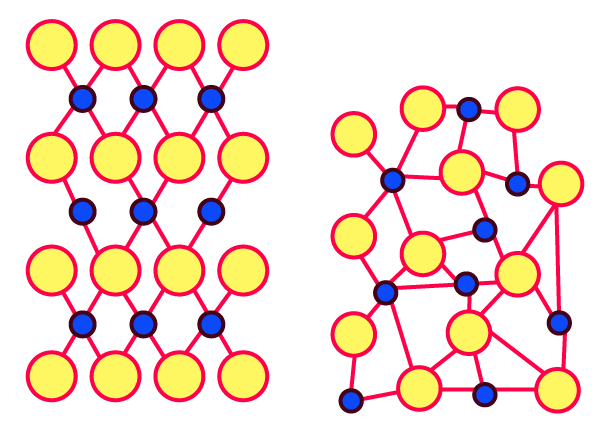
Ans: Image A's arrangement shows that the substance is crystalline. The composition of picture B suggests the substance is amorphous.

Try this. (Textbook Page No.3)

1. Graphite is a covalent solid yet soft and good conductor of electricity. Explain.

Ans: In order to create α bonds and π bonds, each carbon atom in graphite undergoes sp2 hybridization. As a result, hexagonal rings start to form in two dimensions.

The layers of hexagonal carbon networks in graphite are kept together by weak van der Waal forces, which give the material its suppleness.

Due to the pi-bond electrons' delocalisation and freedom to travel within the delocalized molecular orbitals, the ring exhibits strong electrical conductivity.

Can You Recall?

1. What are structures of diamond and graphite?

Ans: The atoms of the carbon compound known as diamond are organised in a diamond cubic crystal form. Diamond hardly ever changes into graphite, a different solid form of carbon that is chemically stable at room temperature and pressure.

2. What are the types of covalent bonds those link carbon atoms in diamond and graphite?

Ans: Two allotropes of carbon are graphite and diamond. A tetrahedral structure and a strong covalent link between the atoms in the diamond's sp3 hybrid state reduce sliding tendency. In contrast, the hexagonal ring-shaped graphite that is undergoing sp2 hybridization is kept in place by weak van der Waals forces.

3. Are all the valence electrons of carbon atoms in graphite localized to specific covalent bonds?

Ans: Carbon atoms in graphite are restricted to a single covalent bond by their valence electrons.

• The excited state of carbon has four valence electrons.

• Only three adjacent carbon atoms in one layer establish covalent connections with one electron remaining free in graphite's carbon structure.

• Graphite becomes a good conductor of electricity as a result of the liberated electrons.

Can You Recall? 

1. What is a hydrogen bond?

Ans: Not a covalent link to a hydrogen atom, hydrogen bonding is a unique kind of dipole-dipole interaction between molecules. It happens when a hydrogen atom is covalently joined to a very electronegative atom, like an oxygen, nitrogen, or fluorine atom, and another extremely electronegative element.

Use Your Brain Power! (Textbook Page No. 13)

1. Which of the three lattices sc, bcc and fcc has the most efficient packing of particles? Which one has the least efficient packing?

Ans: The particle packing in fcc (face-centred cubic) is the most effective, whereas the packing in SCC is the least effective.

Can You Think? (Textbook Page No. 20)

1. When ZnO is heated it turns yellow and returns back to original white colour on cooling. What could be the reason?

Ans: The metal atoms are deposited on the crystal surface of colourless zinc oxide when it is heated to a high temperature, and the anions O2 migrate to the surface to create vacancies at the anion lattice sites. These anions release electrons when they mix with zinc atoms to generate zinc oxide.

Chemical Equation: Zn + O2- → ZnO + 2e-

These liberated electrons enter the crystal, occupy open anion sites, and create F-centres. Zinc oxide turns yellow as a result of these colour centres.

Can You Recall? 

1. What is electrical conductivity?

Ans: The ease with which an electric charge or heat can travel through a substance is measured by its electrical conductivity. A material is considered a conductor if it offers relatively minimal resistance to the flow of thermal or electric energy.

2. What is meant by the terms electrical 'insulator' and 'semiconductor' ?

Ans: Insulators are substances that, under any circumstances, cannot conduct heat or electricity. Wood, rubber, and plastic are good examples of insulators.

A semiconductor is a substance that conducts electricity poorly at low temperatures but better at higher ones. Germanium and Silicon are good examples of semiconductors.

Can You Recall? 

1. How many molecular orbitals are formed by the interaction of two atomic orbitals?

Ans: One Antibonding Molecular Orbital and one Bonding Molecular Orbital are created when two atomic orbitals come together.

2. What is a metallic bond ?

Ans: Valence electrons and metal atoms are attracted to one another through a process known as metallic bonding. Many detached electrons are shared by a large number of positive ions, acting as a sort of a "glue" to bind the molecules together. It differs from ionic or covalent bonding.

Can You Tell? (Textbook Page No. 23)

Let a small quantity of phosphorus be doped into pure silicon.

• Will the resulting material contain the same number of electrons as the original pure silicon?

Ans: Doped silicon will have more electrons overall than pure silicon.

• Will the material be electrically neutral or charged?

Ans: It will be an electrically neutral material.

Importance of Class 12 Chemistry Chapter 1 Exercise Solutions

The chapter, Solid State, is important for students in their Maharashtra Board class 12 for exam preparation. The chapter provides complete information on the physical state of matters- Solid, Liquid, and Gas. It further explains how these matters differ regarding intermolecular or interionic forces having a strong solid state. Once the temperature is raised, solids are converted into liquid, turning them into a gas state after heating. The chapter with solution further explains the representation of equilibrium present in these three states.

In the solution, students will get to learn about types of solids which are divided into two-

• Crystalline Solid is a homogeneous solid in which particles like atoms, molecules, and ions are arranged in a repeat pattern.

• Amorphous Solid- It is a substance appearing solid but does not carry a finely ordered crystalline structure having no regular arrangement of constituent particles.
  
  

With these details in Maharashtra board class 12 chemistry solutions chapter 1 Solid State, students will have a better learning experience. They can practice during the exam and solve questions available in notes. The chapter is quite challenging, but using class 12 chemistry chapter 1 exercise solutions makes the process easy.

Benefits of Class 12 Chemistry Chapter 1 Exercise Solutions

Vedantu experts have prepared this chapter solution keeping the Maharashtra board guidelines in mind. These experts have created important questions that can help students in proper preparation. Moreover, students preparing for engineering entrance can also use the solution note free from the website. Some benefits of downloading the important questions from chapter 1 of Solid State exercise solutions are mentioned below.

• Students will have no trouble preparing for their entrance examination and 12th board exam as they can practice from the prepared set of questions that Vedantu experts created.

• With regular practice, students can grasp the concepts and solve difficult problems in the chemistry chapter Solid State.

• The solid-state exercise solutions with questions and answers formulated keeping the Maharashtra board syllabus in mind. So, students will also have additional help in their exam preparation.
  
  

Download Solid State Chemistry Class 12 Notes PDF Maharashtra Board

Students can download the Solid State chemistry class 12 notes pdf Maharashtra board free from the website. You need to visit the website and download the PDF file of the chapter. You can solve the solution anytime for better preparation. Moreover, you can find additional tips to solve Chemistry solutions.