How to Divide 4 Digit Numbers Using Long Division Method
Today, we will be learning 4-digit divisionsums in the easiest way possible. As we all know that division is one of the basic arithmetic operations where we get a quotient (result) when we divide the dividend with the divisor and if not a whole number, then a remainder.
We use division in cases where we want to divide the quantities or numbers equally or into equal sets and especially in finding out the HCF of given numbers.
An obelus symbol (÷ or /) is used to represent the mathematical operation of division. It is another mathematical operation we use in Arithmetic problems.
Elements of Division
Here's a one-by-one element of long 4-digit division sums with the following example.
Dividend: The dividend is the number you are dividing up with
Divisor: It is the number that is supposed to divide the dividend.
Quotient: It is the final result that we obtain after dividing.
Remainder: If the answer to the division problem is not a whole number; the rest of the number is called the remainder.
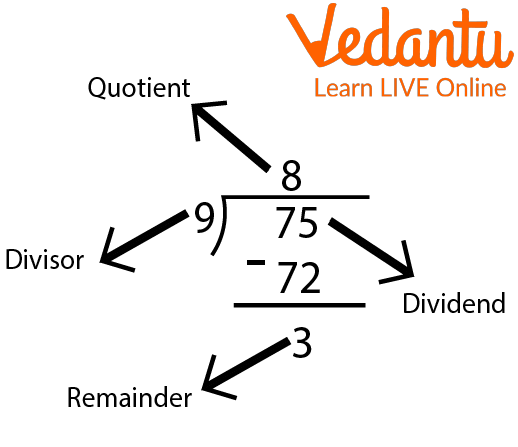
Elements of Division
Important Points to Remember for Division?
If you have an idea of the other 3 mathematical operations listed below and a basic knowledge of divisibility you can master division too!
Multiplication tables till 15
Divisibility rules till 9 (This is optional to know if the number would produce a remainder or not).
Basic Rules to Remember
Any number divided by 0 is infinite ⇒ 1 ÷ 0 = infinite
0 divided by any number is 0 ⇒ 0 ÷ 1 = 0
Adding 0 only when your newest number cannot be divided by the divisor.
Division Process
There is a particular formation according to which allot the numbers to their respective places and that is basically called the placement of the elements. Once we put the numbers in their places next we need to follow a few steps to complete the division method and they are:-
Step 1 - Take the first number of the tip from the left-hand side. Check if this number is lesser than or equal to the divisor.
Step 2 - Also divide it by the divisor and write the answer on top as the quotient.
Step 3 - Abate the result from the number and write the difference below.
Step 4 - Bring down the coming number of the tip( if present).
Step 5 - Repeat the same process until it's non-divisible or you get 0 as the remainder.
Let’s try understanding it with a few examples of how to solve division sums
1. 4980 ÷ 2 =?
We need to divide the number 4980 by 2 which means 2 is the divisor and 4980 is the dividend.
The number in the thousands place value which is 4 is greater than 2 so, no need to take two digits at a time and 4 is a multiple of 2 as well so, therefore, we take the number directly and 0 is put in the quotient's place.
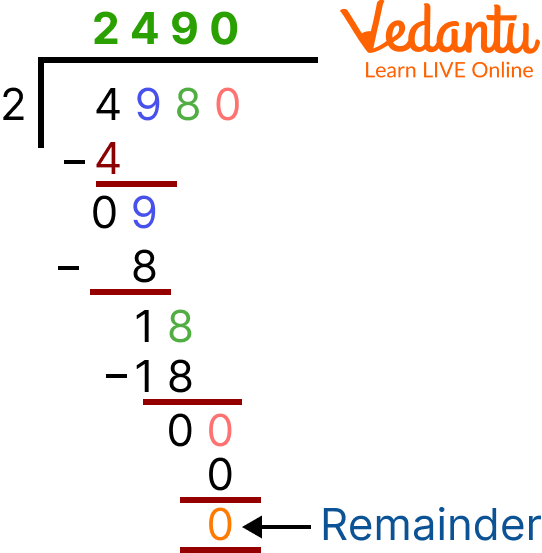
Example 1 of Division Steps
4980 ÷ 2 = 2490
2. 9001÷3 =?
The divisor is 3 and the dividend is 9001; so, we will place them according to their places.
Note: We put 0 in the quotient when a number is completely divided and the remainder that we get is 0. Putting the 0 simultaneously in the quotient’s place as well; So basically considering 9000 (round of 9001) as a multiple of 3. For better understanding follow the image shown below. Putting point ( . ) in the quotient’s place means we can add 0 as the one place to the dividend.
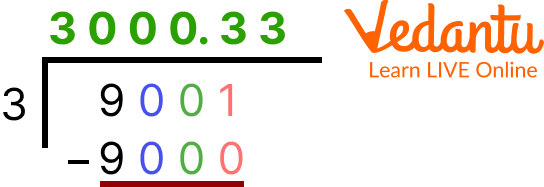
Example 2 of Division Steps
If the quotient goes into decimals, then it is better to consider only two numbers after the point or round of those two numbers also works.
Ans: 9001 ÷ 3 = 3000.33
3. $\dfrac{2272}{4}$
The divisor is 4 and the dividend is 2272; so, we will place them according to their places.
$\dfrac{2272}{4} = 568$
The remainder will be zero and the quotient is 568.
4. $\dfrac{7128}{9}$
The divisor is 9 and the dividend is 7128; so, we will place them according to their places.
$\dfrac{7128}{9} = 792$7128/9 = 792
The remainder will be 0, the quotient is 792.
5. $\dfrac{2335}{5}$
The divisor is 5 and the dividend is 2335; so, we will place them according to their places.
$\dfrac{2335}{5} = 467$
The remainder is 0, the quotient is 467.
Practice Questions
How do solve these four-digit division sums?
Q 1. $\dfrac{5090}{4}$
Ans:1272.5
Q 2. $\dfrac{7080}{12}$
Ans: 590
Q 3. $\dfrac{2103}{9}$
Ans:233.67
Q 4. $\dfrac{4312}{5}$
Ans: 862.4
Q 5. $\dfrac{7094}{7}$
Ans: 1013.42
Summary
In this article, proper steps of the 4-digit number long division method are shown with the use of a few examples for better understanding. The division is a basic mathematical operation where a larger number is split into smaller numbers containing equal groups. Basic rules of division have also been explained along with the division steps.
It is a very useful method with its own application as per the need. A vast number of examples are available to practice the 4-digit division sums and anyone can easily solve them. We will come up with more easy methods to solve mathematical operations and problems so keep visiting our blog for more updates.
FAQs on Division of 4 Digit Numbers Explained Simply
1. What is 4 digit numbers division?
4 digit numbers division is the process of dividing a four-digit number (1000–9999) by another number to find the quotient and possibly a remainder. It is usually done using the long division method.
- The dividend is the 4-digit number.
- The divisor can be 1-digit, 2-digit, or more.
- The result is expressed as: Dividend ÷ Divisor = Quotient + Remainder.
2. How do you divide a 4 digit number by a 1 digit number?
To divide a 4 digit number by a 1 digit number, use the long division method step by step from left to right.
- Step 1: Divide the first digit (or first two digits if needed).
- Step 2: Multiply the divisor by the quotient digit.
- Step 3: Subtract.
- Step 4: Bring down the next digit.
- 57 ÷ 8 = 7 (7 × 8 = 56)
- Subtract → 57 − 56 = 1
- Bring down 2 → 12 ÷ 8 = 1
- Bring down 8 → 8 ÷ 8 = 1
3. How do you divide a 4 digit number by a 2 digit number?
To divide a 4 digit number by a 2 digit number, estimate carefully and apply the long division steps.
- Step 1: Check how many digits of the dividend are needed to divide.
- Step 2: Divide, multiply, and subtract.
- Step 3: Bring down the next digit.
- 34 ÷ 12 = 2 (2 × 12 = 24)
- Subtract → 34 − 24 = 10
- Bring down 5 → 105 ÷ 12 = 8
- Bring down 6 → 96 ÷ 12 = 8
4. What is the formula for division?
The basic division formula is Dividend ÷ Divisor = Quotient.
- If there is a remainder: Dividend = (Divisor × Quotient) + Remainder.
- The remainder is always less than the divisor.
5. Can you give an example of a 4 digit division with remainder?
Yes, a 4 digit division can result in a remainder when the number does not divide exactly.
- Example: 7895 ÷ 6
- 7895 ÷ 6 = 1315 remainder 5
- Check: (6 × 1315) + 5 = 7895
6. What are the steps of long division for large numbers?
The steps of long division for large numbers follow the pattern Divide → Multiply → Subtract → Bring Down.
- Divide the current number.
- Multiply the divisor.
- Subtract the product.
- Bring down the next digit.
7. How do you check the answer of a 4 digit division?
You can check a 4 digit division by using the formula Dividend = (Divisor × Quotient) + Remainder.
- Multiply the divisor and quotient.
- Add the remainder (if any).
- The result must equal the original dividend.
8. What are common mistakes in dividing 4 digit numbers?
Common mistakes in 4 digit numbers division include incorrect subtraction and wrong placement of quotient digits.
- Forgetting to bring down the next digit.
- Misplacing digits in the quotient.
- Errors in multiplication or subtraction.
- Ignoring the remainder.
9. Can a 4 digit number be divided exactly?
Yes, a 4 digit number can be divided exactly when the remainder is 0.
- This happens when the divisor is a factor of the number.
- Example: 9600 ÷ 12 = 800.
- Since the remainder is 0, it is an exact division.
10. How do you estimate 4 digit division quickly?
You can estimate 4 digit division by rounding numbers to make mental calculation easier.
- Round the dividend and divisor to nearby friendly numbers.
- Divide the rounded numbers.
- Adjust if necessary.
