




Step-by-Step Guide to Constructing the Circumcircle
A plane figure in which a point is taken as the centre and from that point dots which are equidistant are marked and then joined which makes a circle. The first point or the reference point is known as a centre and the distance between the centre and the surrounding path is known as the radius of the circle.

Radius of a Circle
The circle which encircles a polygon by touching each vertex of the polygon is termed a circumcircle. It is drawn by taking the meeting point of the perpendicular bisector to the sides of the polygon as the centre.
What is Circumcircle?
A circumcircle is a circle which circumscribes any polygon and touches each vertex of the polygon. The radius of the circumcircle is the distance between the point of meeting of bisectors and the vertex. The circumcircle is drawn by taking the meeting point of the perpendicular bisector to the sides of the polygon as the centre.
The Circumcircle of a Triangle Formula
The circumcircle of a triangle can be simply derived using the following various methods. The formula is not universal since it changes based on the type of triangle. So let’s find out more about how to find the circumcircle of a triangle.
The Circumcircle of a Triangle
For example, we have to draw a circumcircle to the given triangle then the following steps must be followed;
Step 1: Draw the perpendicular bisectors of the sides.
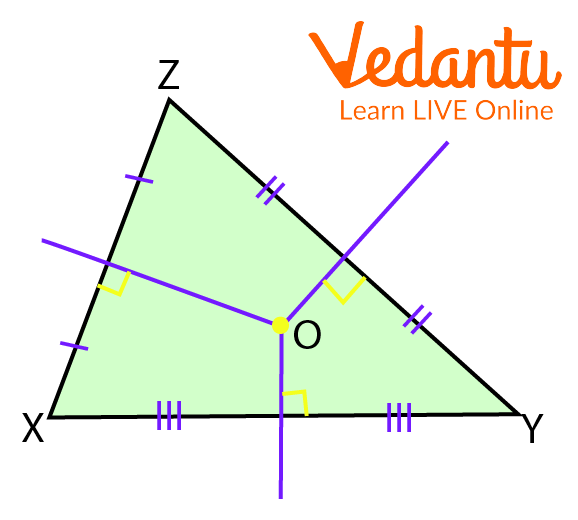
Circumcircle around a Triangle
Step 2: Taking point O as the centre we draw a circle which touches each vertex of the triangle.
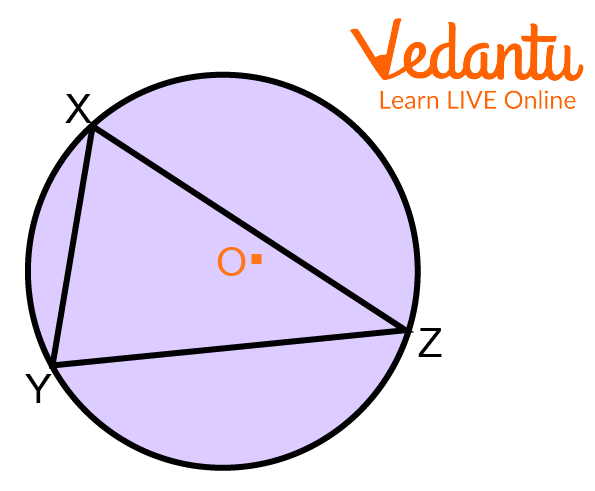
Process of Drawing a Circumcircle Around a Triangle
Step 3: The distance OZ, OX and OY is said to be the circumradius.
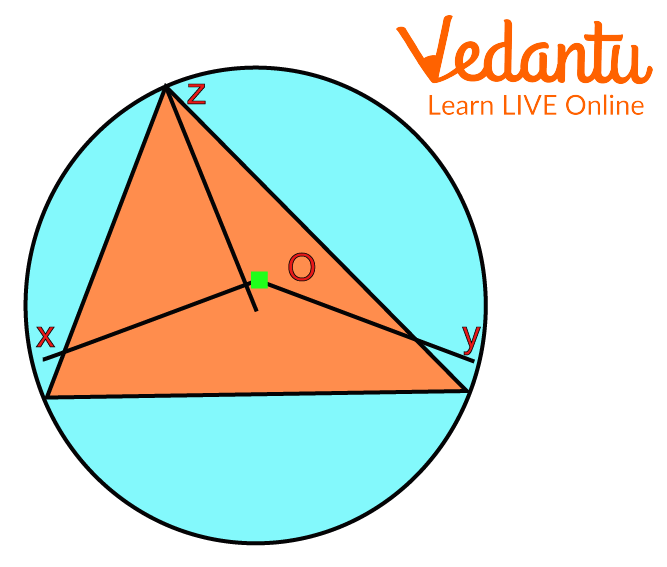
Circumcentre
Hence, the required circumcircle is as above with the circumcentre as O.
Circumradius of Right Angle Triangle
The Circumradius of the right angle triangle is the radius of the circle of the circumcircle which is drawn around a polygon. Let us draw a circumcircle for the right-angled triangle.
Step 1: Take a right-angled triangle.

Right-angled Triangle
Step 2: Draw the perpendicular bisector of the sides of the triangle.

Perpendicular Bisector
Step 3: Taking the meeting point of the perpendicular bisector and the vertex which is most distant from it as a radius, draw a circle which passes through each vertex of the triangle.
Right-angled Triangle in a Circumcircle
Hence, the circumcircle of the given right-angled triangle with circumradius “R” is as depicted in the figure above.
How to find the Circumradius of a Triangle?
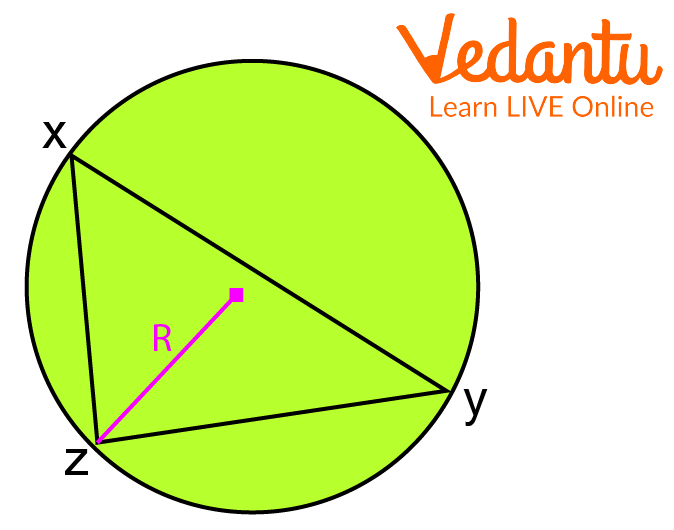
Let that there is a circumcircle which is circumscribing a triangle with sides a, b and c with a circumcentre.
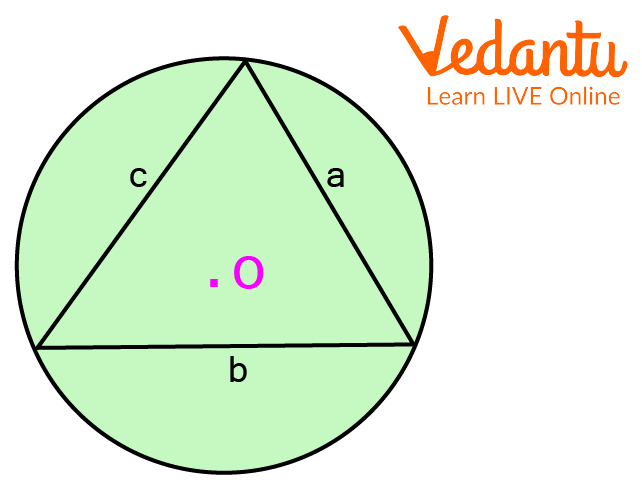
Circumcircle Circumscribing a Triangle
$2 \mathrm{R}=\dfrac{a}{\operatorname{Sin} A}=\dfrac{b}{\operatorname{Sin} B}=\dfrac{c}{\sin C}$
Now, Area of triangle $\left(A_{t}\right)=\dfrac{1}{2} a b \operatorname{Sin} C$
$\operatorname{Sin} C=\dfrac{C}{2 R}$
Therefore, $\mathrm{A}_{\mathrm{t}}=\dfrac{1}{2} a b \dfrac{C}{2 R}$.
Now, $\mathrm{R}=\dfrac{a b c}{4 A}$
Hence, the required formula to find the circumradius of the triangle is $\mathrm{R}=\dfrac{a b c}{4 A}$.
Solved Questions
Q1. List all the steps in drawing a circumcircle of a triangle.
Ans: To draw a circumcircle of a triangle follows the steps below:
Step 1: Draw the perpendicular bisectors of the sides
Step 2: Taking point O as the centre we draw a circle which touches each vertex of the triangle.
Step 3: The distance between OZ, OX and OY is said to be the circumradius.
Q2. Draw the circumcircle of a triangle with sides of 6 cm, 8 cm and 10 cm. What is the radius of this circle?
Ans: 5 cm
Steps for construction:
Step 1: Construct ΔABC with AB = 6 cm, BC = 8 cm and CA = 10 cm.
Step 2: Draw the perpendicular bisectors of any two sides of the triangle (say, AB and BC).
Step 3: Find the point of intersection of the perpendicular bisectors and mark it as O.
Step 4: Measure the distance OA or OB or OC, they are all equal to the radius of the circumcircle.
Step 5: OA = OB = OC = 5 cm
Practice Questions
Q1. Considering the given statement states whether it is true or false with reason: “A circle drawn inside a triangle touching all its sides is known as a circumcircle.”
Ans: False
Q2. Circumradius is the distance between the meeting point of the bisector of sides of a polygon and the vertex. True or False explain with reason.
Ans: True
Q3. Circumcentre of a circle is the point of concurrency of the
(a) angular bisectors of vertices
(b) medians
(c) perpendicular bisectors of sides
(d) any two sides
Ans: (c) perpendicular bisectors of sides
Q4. The ratio of the area of the circumcircle and incircle of an equilateral triangle is
(a) 4:1
(b) 1:4
(c) 9:1
(d) 1:9
Ans: (a) 4:1
Summary
After reading this article you must have been very well aware of the concepts of the circumcircle, circumradius, how to draw a circumcircle of a triangle and about circles. These concepts will help in solving problems of geometry and Circles in your textbook. You have also learnt the relationship between the radius of the circumcircle and the area of the triangle. We have learnt that a circle that touches the vertex of the triangle and is drawn outside the triangle is known as a circumcircle. But when a circle touches the sides of the triangle and is drawn inside the triangle it is known as a circle. The distance between the meeting point of the bisector of sides and the vertex is known as the circumradius.
FAQs on Circumcircle of a Triangle Explained
1. What is the circumcircle of a triangle explained in simple terms?
The circumcircle of a triangle is the unique circle that passes through all three of its vertices (corners). Every triangle, regardless of its shape or size, has exactly one circumcircle. The center of this circle is called the circumcenter, and its radius is known as the circumradius.
2. What are the circumcenter and circumradius of a triangle?
The circumcenter and circumradius are key properties related to the circumcircle:
- Circumcenter: This is the exact center of the circumcircle. It is found at the point where the perpendicular bisectors of the triangle's three sides intersect.
- Circumradius: This is the radius of the circumcircle. It is the distance from the circumcenter to any of the three vertices of the triangle. This distance is the same for all three vertices.
3. What is the main formula to find the circumradius (R) of a triangle?
The most common formula to calculate the circumradius (R) of any triangle is:
R = (a × b × c) / 4Δ
Where:
- a, b, and c are the lengths of the three sides of the triangle.
- Δ (Delta) is the area of the triangle.
4. How does the location of the circumcenter change for different types of triangles?
The position of the circumcenter depends on the triangle's angles, which is an important concept:
- For an acute triangle (all angles less than 90°), the circumcenter lies inside the triangle.
- For a right-angled triangle, the circumcenter lies exactly at the midpoint of the hypotenuse (the longest side).
- For an obtuse triangle (one angle greater than 90°), the circumcenter lies outside the triangle.
5. How can you construct the circumcircle of a triangle using a compass and ruler?
You can construct a circumcircle with the following steps:
- Step 1: Draw the perpendicular bisector for any two sides of the triangle. A perpendicular bisector is a line that cuts a side into two equal halves at a 90° angle.
- Step 2: The point where these two perpendicular bisectors intersect is the circumcenter (O).
- Step 3: Place the compass point at the circumcenter (O) and set its width to any one of the triangle's vertices (e.g., A). This distance is the circumradius (R).
- Step 4: Draw the circle. It will perfectly pass through all three vertices A, B, and C.
6. What is the key difference between a circumcircle and an incircle of a triangle?
The primary difference lies in what they connect to:
- A circumcircle is drawn around the outside of a triangle and passes through its three vertices. Its center (circumcenter) is found from the intersection of the perpendicular side bisectors.
- An incircle is drawn inside a triangle and touches its three sides. Its center (incenter) is found from the intersection of the angle bisectors.
7. Why is the circumcenter equidistant from all three vertices of the triangle?
This is due to a fundamental property of perpendicular bisectors. The circumcenter is the point where all three perpendicular bisectors meet. Any point on the perpendicular bisector of a line segment is always equidistant from the two endpoints of that segment. Since the circumcenter lies on the perpendicular bisector of all three sides, it must be equidistant from all three pairs of vertices, and therefore, from all three vertices simultaneously.
8. Is there a simpler formula for the circumradius of a right-angled triangle?
Yes, for a right-angled triangle, the circumcenter is the midpoint of the hypotenuse. Therefore, the circumradius (R) is simply half the length of the hypotenuse. The formula is:
R = Hypotenuse / 2
This provides a much quicker way to find the circumradius without needing to calculate the triangle's area.





































