Addition and Subtraction of Fraction

A fraction is defined as a part of the whole. We do addition and subtraction of fractions in our daily life also. Let us understand it with the help of an example.

Riya orders a pizza. When the pizza arrived, Riya saw that the pizza was divided into six equal pieces. She decided to eat two pieces of pizza for lunch and store the rest. After a few hours, she decided to eat one more piece of pizza. Can you tell how many pieces of Pizza she ate? Yes, you are right. She ate three pieces of pizza out of 6 six pieces which mean she ate half of the pizza.

Addition of Fraction Shown by Adding Pieces of Pizza.

Addition and Subtraction of Fractions

All fractions are not added or subtracted in the same way. There are different ways to add or subtract different types of fractions depending on certain conditions.

• Condition 1. When fractions have the same denominator

• Condition 2. When fractions have different denominators

Addition or Subtraction of Fractions with the Same Denominator

Fractions with the same denominators are called fractions, and adding and subtracting them is very easy.

Example 1: $\dfrac{1}{5} + \dfrac{2}{5}$= ?

The above example is an example of like fractions because the denominator is the same.

In such cases, all you have to do is to focus on numerators and add the numerator.

1+2 = 3

Therefore, $\dfrac{1}{5} + \dfrac{2}{5}$= $\dfrac{3}{5}$

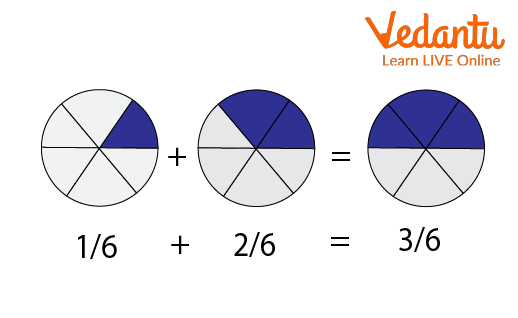
Addition of Like Terms.

You have to follow the same method with subtraction also.

Example 2: $\dfrac{5}{7} - \dfrac{2}{7}$ =?

we know that these are like Fractions and

5-2= 3

Therefore $\dfrac{5}{7} - \dfrac{2}{7}$= $\dfrac{3}{7}$

Addition or Subtraction of Fractions with Different Denominators

We have to add a subscription to the fractions with different denominators. The first that we have to do is convert unlike fractions into like fractions.

For converting fractions into like fractions, we have to do the following steps.

Example 1: $\dfrac{27}{4} + \dfrac{29}{8}$ = ?

• To convert the Unlike fraction into a like fraction, we must take out the LCM of the denominators.

In this case, the LCM of 4 and 8 is 8.

• The next step is to divide the denominator of the fraction with LCM.

For $\dfrac{27}{4}$ ,

$\dfrac{8}{4}$= 2

Multiply the resulting number with the numerator and denominator of the fraction

$\dfrac{27}{4} \times \dfrac{2}{2}$ = $\dfrac{54}{8}$

Repeat the process with the other fraction

For $\dfrac{29}{8}$

$\dfrac{8}{8} = 1$

Multiplying numerator and denominator with the given number

$\dfrac{29}{8} \times \dfrac{1}{1}$ = $\dfrac{29}{8}$

Now since both the numbers are converted into like fractions

$\dfrac{27}{4}$ becomes $\dfrac{54}{8}$

$\dfrac{29}{8}$ remains $\dfrac{29}{8}$

• On adding these $\dfrac{54}{8} + \dfrac{29}{8} = \dfrac{83}{8}$

Therefore $\dfrac{27}{4} + \dfrac{29}{8} = \dfrac{83}{8}$

Let us understand one example of subtraction with unlike fractions also.

Example 2: $\dfrac{3}{4} - \dfrac{1}{6}$ = ?

• The first step to converting unlike fractions into like fractions is to take the LCM of the denominator.

In this case, the LCM of 4 and 6 is 12.

• The next step is to divide the denominator of the fraction with the LCM.

For $\dfrac{3}{4}= \dfrac{12}{4} = 3$

Multiply the resulting number with the numerator and denominator of the fraction so $\dfrac{3}{4} \times \dfrac{3}{3} = \dfrac{9}{12}$

Complete this step with attraction also.

For $\dfrac{1}{6}= \dfrac{12}{6} = 2$

Now, $\dfrac{1}{6} \times \dfrac{2}{2} = \dfrac{2}{12}$

Therefore,

$\dfrac{3}{4}$ becomes $\dfrac{9}{12}$

$\dfrac{1}{6}$ becomes $\dfrac{2}{12}$

• Subtract like fractions.

$\dfrac{9}{12} - \dfrac{2}{12} = \dfrac{7}{12}$

Therefore, $\dfrac{3}{4} - \dfrac{1}{6} = \dfrac{7}{12}$

Practice Questions

1. $\dfrac{15}{83} + \dfrac{20}{83}$

Ans: $\dfrac{35}{83}$

2. $\dfrac{7}{8} + \dfrac{3}{4}$

Ans: $\dfrac{13}{8}$

3. $\dfrac{2}{8} + \dfrac{2}{4}$

Ans: $\dfrac{3}{4}$

4. $\dfrac{7}{9} - \dfrac{11}{45}$

Ans: $\dfrac{8}{15}$

5. $\dfrac{1}{11} + \dfrac{2}{12}$

Ans: $\dfrac{17}{66}$

Summary

Fractions are part of a whole, and adding or subtracting fractions is something we use in everyday life. Fractions are added or subtracted in different ways depending if they are like fractions or unlike fractions.

Like fractions are those fractions that have the same denominator, and unlike fractions are those fractions that have different denominators. We will get to know what fractions are, the different types of fractions, how to subtract a fraction, etc. There are a few solved examples that will help you to understand the concept of fractions better. fraction subtraction examples are also there.