What is the Area of Rectangle?
Do you have a book or a laptop in front of you? Notice its shape! It’s a rectangle. Do you see all four sides to be equal? No, right? A rectangle has two sides, length (L) and Breadth (B). The length of a rectangle is the longest side, whereas the range is the shortest side. The range of a rectangle is occasionally pertained to as the breadth (b).
Length and breadth are the tools that are used to find the confines of an object. When we relate to two-dimensional shapes (2D shapes), we use length and breadth. Continue reading to know more about rectangles.
What are Length and Width?
Before we proceed further, let us first understand what the following two terms mean.
Length: Length is used to scale the distance between two points. It is the lengthy size of a figure, and it shows how long the given object or figure is. It's expressed in direct units like measures, centimetres, elevation, etc.
Width: Width is the shorter length of an object or a figure, and it shows how broad or wide the given figure is. The range is also expressed in direct units like measures, centimetres, elevation, etc.
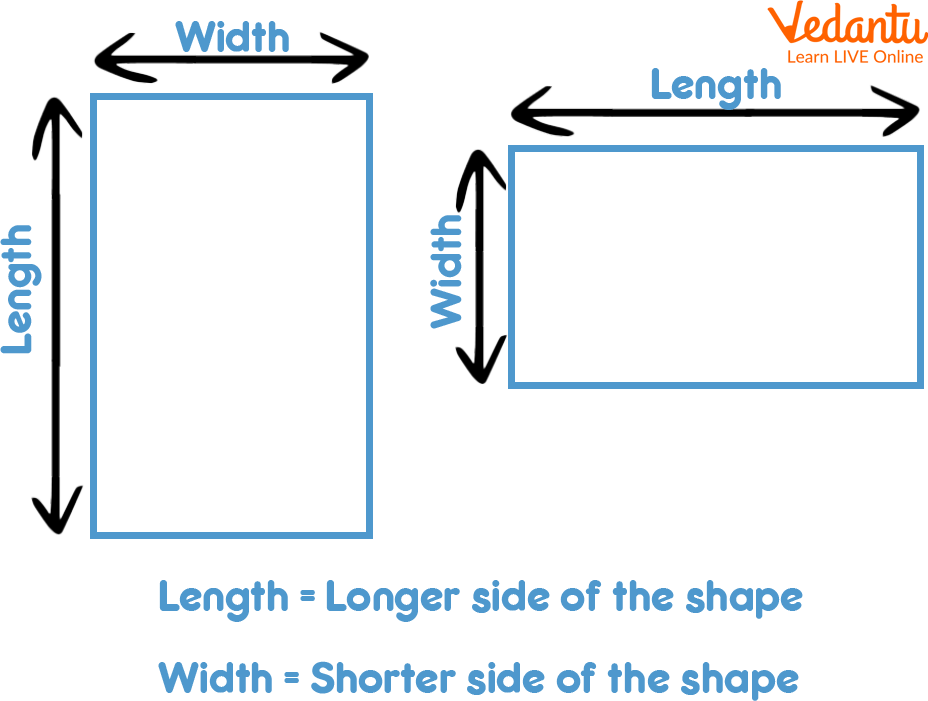
Length and Width
Area of a Rectangle
In the below figure, the area of the rectangle is the region covered by the rectangle in a two-dimensional plane. A rectangle is a quadrilateral, a 2-D shape with four sides and four vertices. All four sides of the rectangle are right sides or equal to 90 degrees. The opposite sides of the rectangle are equal and resemblant to each other. When observed, a parallelogram also has its opposite sides equal and resemblant to each other, but the angles aren't equal to 90 degrees.
Rectangle
What is the Area of a Rectangle?
The area of a rectangle is the region covered by a rectangle within its four sides or boundaries. The region of a rectangle depends on its sides. Principally, the formula for area is equal to the product of the length and breadth of the rectangle. However, when we speak about the border of a rectangle, it's equal to the sum of all its four sides. Hence, the region enclosed by the rectangle's border is its area.
Area of rectangle = Length x Breadth
A = l x b
Area of Rectangle Formula
The formula to find the area of a rectangle depends on its length and range. The area of a rectangle is calculated in units by multiplying the range (or breadth) by the Length of a rectangle. Side and total face areas can be calculated only for three-dimensional figures. We cannot calculate the rectangle since it's a two-dimensional figure. Therefore, the border and the area of a rectangle are given by:
The formula for the area of a rectangle is as follows:
A = l × b
Area of Rectangle Units
The area of a rectangle can be calculated by numbering the piece of small full places of measurement 1 * 1sq. units needed to fill in the rectangle.
When multiplying the length by the range, always ensure you work in the same unit of length. However, modify them to the same unit if given in different units.
Steps to Find the Area of a Rectangle
Follow the steps given below to determine the area of a rectangle:
Step 1: Note the values of length and range from the given data.
Step 2: Multiply length and range values.
Step 3: Write the results in square units.
Length and Breadth Formula
Length Formula
When we want to detect the length of a rectangle, we require to divide the area by breadth.
Length = Area ÷ breadth
ℓ = A ÷ b
The introductory formula for risking the length of a rectangle when we're contributing the breadth and area is only to divide the area by breadth.
Breadth Formula
When we want to find the breadth of a rectangle, we require to divide the area by length.
Breadth = Area ÷ length
b = A ÷ l
The primary formula for risking the breadth of a rectangle when we've presented the length and area is to only divide the area by length.
Solved Examples
Q 1. Find the area of a rectangle whose width is 20 cm and length is 4 cm.
Ans: Given, width = 20 cm and length = 4 cm
Area = w × l
Area = 20 × 4
thus, the area of the rectangle = 80 cm2.
Find the area of the rectangle whose length is 15 cm and the range is 4 cm.
result
Given,
Length = 15 cm
Range = 4 cm
Area of a rectangle = Length × range
15 × 4 = 60
Hence, the area of the rectangle = 60 cm2
Q 2. The length of a blockish screen is 15 cm. Its area is 180sq. cm. Find its width.
Ans: Area of the screen = 180 sq. cm.
Length of the screen = 15 cm
Area of a rectangle = length x range
So, width = area/ length
Therefore, width of the screen = 180/15 = 12 cm
Practice Questions
Q 1. Find the area of a rectangle whose width is 10 cm and length is 2 cm.
Ans: 20 cm2
Q 2. Find the area of a rectangle whose width is 30 cm and length is 4 cm.
Ans: 120 cm2
Summary
A rectangle is a four-sided shape with two pairs of parallel sides. It is the most basic shape which has many uses in Maths and everyday life. A rectangle is characterised by length (L) and width/ breadth (W). Both length and width are different in size. The area is the region covered by a two-dimensional shape in a plane. It's measured in square units. Thus, the area of the rectangle is the region enclosed by its external boundaries. It's equal to the product of length and width.
FAQs on Area of Rectangle
1. How can I find the area of a rectangle with the help of its diagonals?
The diagonal of a rectangle is a straight line that connects its opposite vertices. The total number of diagonals in a rectangle is two both of which are of equal lengths. The diagonal of a rectangle can be calculated using the pythagorean theorem.
\[\text{(Diagonal)}^{2} = \text{(Length)}^{2} + \text{(Breadth)}^{2}\]
\[\text{(Length)}^{2} = \text{(Diagonal)}^{2} - \text{(Breadth)}^{2}\]
\[\text{Length} = \sqrt{\text{(Diagonal)}^{2} - \text{(Breadth)}^{2}}\]
Now, Area of a rectangle is l x b
Therefore, the area of a rectangle using its diagonals can be calculated with the formula-
\[\text{Area of rectangle} = \text{Breadth} \sqrt{\text{(Diagonal)}^{2} - \text{(Breadth)}^{2}}\]
2. What is the perimeter and what is the perimeter of a rectangle?
The perimeter of a figure gives the total length of its boundaries. For example- the perimeter of a square will be the sum of its all four sides.
Similarly, the perimeter of a rectangle will be the sum of its length and width. The opposite side, which means the length and width of a rectangle are equal. Therefore, the perimeter of the rectangle will be the sum of the product of its lengths and the product of its widths.
Suppose the length and width of a rectangle are a and b respectively
Perimeter P = Sum of all sides
P = a+b+a+b
P = 2a + 2b
P = 2(a +b)
3. What are the important formulas related to rectangles?
It is very important for the students to learn all the formulas related to rectangles in order to do calculations. Some of the basic formulas for rectangles are-
Quantity | Formula |
Area of the rectangle (A) | \[l\times b\] |
Perimeter of rectangle (P) | $2({l}\times{b})$ |
Length of rectangle (l) | \[\frac{A}{b}\] |
Length of rectangle (l) | \[\frac{P}{2}-b\] |
Breadth of rectangle (b) | \[\frac{A}{l}\] |
Breadth of rectangle (b) | \[\frac{P}{2}-l\] |
Diagonal of rectangle | \[\sqrt{(l)^2+(b)^2}\] |
To know more about the rectangle formula students can visit Vedantu’s study material on Rectangle Formulas.
4. What are the properties of a rectangle?
The properties of a rectangle are-
Rectangle is a quadrilateral in which all the four interior angles are equal.
The opposite sides of a rectangle which are commonly known as length and breath are equal and parallel to each other.
The interior angles measure 90o at each vertex of a rectangle.
All the interior angles in a rectangle when added equal to 360o.
There are two equal diagonals in a rectangle that are bisecting.
A rectangle is also called a parallelogram since all the opposite sides are parallel.
All rectangles are known to be parallelograms but all parallelograms cannot be rectangles.
5. The dimensions of one stone slab is 25 cm long and 10 cm broad. How many pieces of stone slabs are required in order to lay a path which is 250 m long and 15 m wide.
For one slab,
length = 25 cm
breadth = 10 cm
\[ \text{Area of one slab}\] = \[25 \times 10\]
Area of one slab = 250 cm2
For the path,
length = 250 m
breadth = 15 m
\[ \text{Area of the path}\] = \[250 \times 15 \times 10000 cm ^{2}\]
\[ \text {Required number of slabs}\] = \[ \frac{ \text {Area of path}} { \text {Area of each slab}}\]
\[ \text {Required number of slabs}\] = \[ \frac{250 \times 15 \times 10000} {250}\]
Required Number of Slabs = 150000 |
6. Can a square be called a rectangle?
A rectangle is a quadrilateral with all equal angles that are right angles. In addition to having all equal angles, a square also has all equal sides. As a result, a square is a subset of a rectangle. In other words, a rectangle can also be a square (when all sides are equal).
7. Which shape is both a rectangle and a square?
A square is a rectangle and a rhombus since it has the features of both a rectangle and a rhombus.