Decimal Expansion of Rational Numbers

Let's first define rational numbers before discussing how they are represented when expanded to decimal form. The term "rational number" refers to any number that can be expressed as $\dfrac{p}{q}$, where $p$ and $q$ are integers and $q\neq 0$. Decimals are what is produced when these numbers are further simplified. Let’s learn more about the decimal expansion of rational numbers through this article.

Examples: $3, -5.8, \dfrac{4}{6}$.

Decimal Expansion of the Rational Number

The decimal expansion of a rational number is obtained by dividing the numerator by the denominator of the rational number.

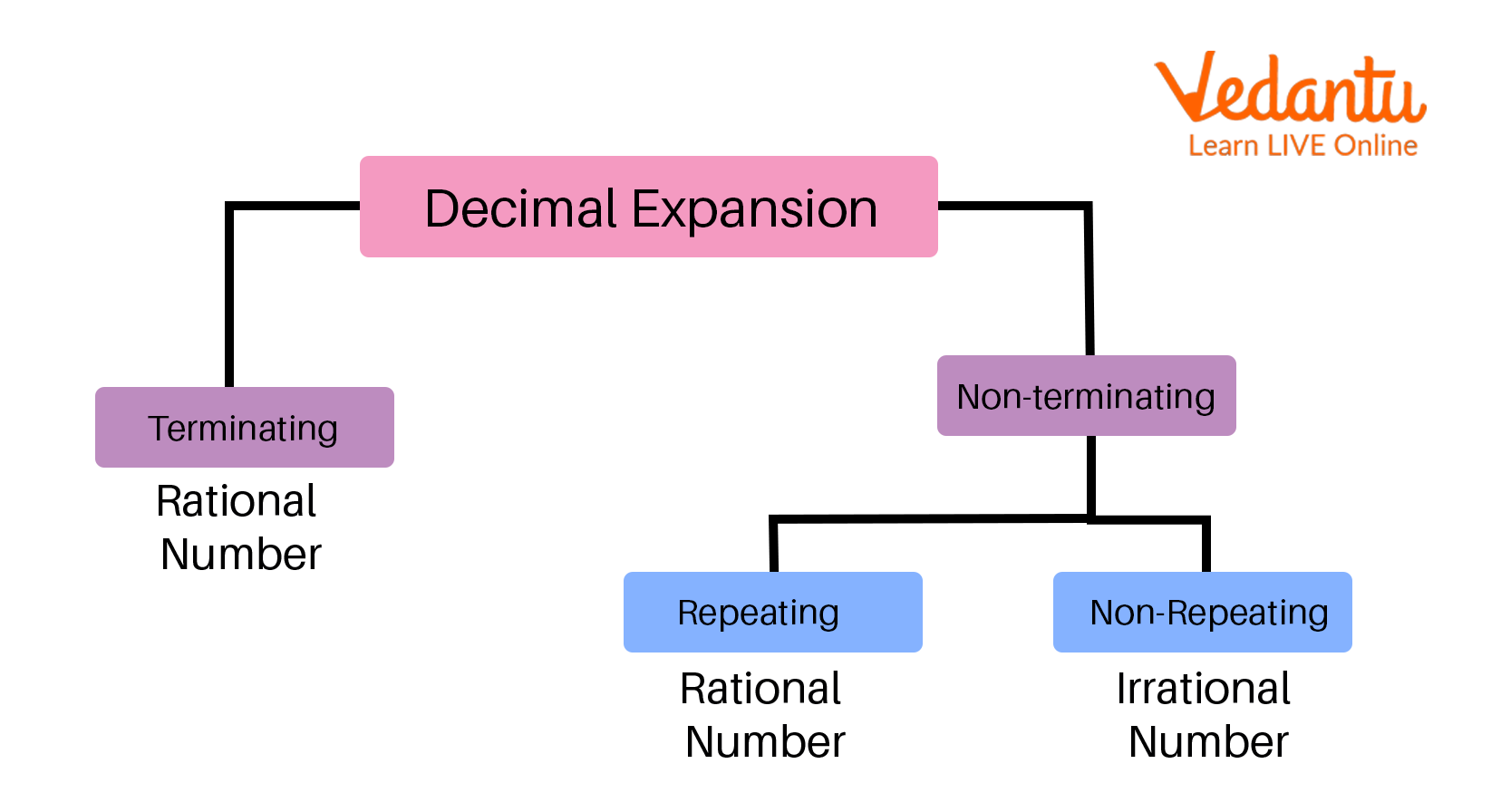
Decimal Expansion

Types of Decimal Expansion

By dividing a rational number's numerator by its denominator, one can get the decimal expansion of a rational number. Two types of decimal numbers may result from this process.

1. Terminating Decimal Numbers

2. Non-Terminating Decimal Numbers

• Terminating Decimal Numbers: Terminating decimal numbers are those decimal numbers with a limited number of digits following the decimal point. These decimal integers can be expressed in the $\dfrac{p}{q}$ form, where $q$ is not equal to $0$.

For example,

$2.4, 4.436$ are the terminating decimal numbers.

$2.4$ is represented as $\dfrac{24}{10}$.

Here, $p=24$ and $q=10$ and the number of decimal places $=1$.

• Non-terminating Decimal Numbers: Non-terminating decimal numbers are those that have an endless number of digits following the decimal point.

Non-terminating decimal numbers include, for instance, $0.3333…, 4.53333…, and 5.3431034310…$.

How to Expand Rational Numbers in Decimals

Whole numbers, natural numbers, and integers are all examples of rational numbers because they can all be expressed in $\dfrac{p}{q}$ form, as we have explained. Decimal numbers that are stated as rational numbers may be repeating decimals that terminate or do not.

Example: Find the decimal expansion of $\dfrac{1}{3}$.

Let's divide the numerator by the denominator.

Decimal Expansion

$\dfrac{1}{3}$ is expanded to its decimal value of $0.333333$.

In this case, the divisor is $3$, and each step's remainder is $1$.

Terminating Decimal Expansion of Rational Numbers

When the digits after the decimal point are either terminated or finite, a number has a terminating decimal expansion. The decimal expansion for the fraction $\dfrac{5}{10}$ is $0.5$, which is known as a terminating decimal expansion since digits after the decimal point stop after one digit.

Non-terminating Decimal Expansion of Rational Numbers

The term "repeating" or "recurring" indicates that the repetition of the decimal values leads to a recognisable pattern that is easy to recognise, even though the decimal places in this expansion will never end and carry on forever. The expression $dfrac29=0.2222222$ is an illustration of a non-terminating recurring decimal expansion. For example, $0.222222...$ can also be written as $overline0.2$, demonstrating decimal repetition.

Non-terminating Decimal Expansion

Irrational Numbers Decimal Expansion

The use of decimal numerals to indicate an irrational number's most accurate value is referred to as the "decimal representation of irrational numbers." Non-terminating decimals with non-repeating digits are used to represent irrational numbers. For instance: Let's consider $\sqrt{2}$.

Attempting to write $\sqrt{2}$. For example, to $5$ decimal digits in decimal form, we have

$\sqrt{2} = 1.41421…$ If we enlarge √$\sqrt{2}$ to $10$ decimal places then we get $\sqrt{2}=1.4142135623…$

Interesting Facts

• Any number that can be stated as a fraction is rational.

• The examples include rational numbers: whole numbers, integers, fractions of integers, and terminating decimals.

• Rational numbers also include recurring decimal patterns and non-terminating decimals.

• A fraction is regarded as negative if it has a negative sign, either in the numerator, the denominator, or the fraction itself.

Solved Examples

Example 1: How would you characterize the prime factorization of the denominator of 42.123456789?

Solution: Since 42.123456789 is a decimal number with a terminating expansion, its denominator has the form $2^m 5^n$, where $m$ and $n$ are positive integers.

$43.123456789 =\dfrac{43123456789}{1000000000}$

$=\dfrac{43123456789}{(10)^9} \\$

$=\dfrac{43123456789}{(2 \times 5)^9} \\$

$=\dfrac{43123456789}{2^9 \times 5^9}$

Hence, it has prime factorisation in the terms of 2 and 5.

Example 2: How many digits does the rational number $\dfrac{1}{2^6 \times 5^2}$ end-on?

Solution: Let's use a whole number as the denominator.

$\dfrac{1}{2^6 \times 5^2}\\$

$=1\times \dfrac{(5^4)}{(2^6 \times 5^2 \times 5^4)}\\$

$=\dfrac{625}{2^6 \times 5^6}\\$

$=\dfrac{625}{1000000}\\$

$=0.00000625$

The supplied rational number thus comes to an end at six decimal digits.

Practice Questions

1. Which of the following is the decimal representation of $\dfrac{5}{13}$ ?

1. $0.\overline{384615}$

2. $0.384384$

3. $0.\overline{384}$

4. None of these

2. 0 is not a

1. Rational number

2. Irrational number

3. Whole number

4. Natural number

Answers

1. (A)

2. (D)

Summary

Let's summarise everything we've learnt in this article. Fractions can be used to represent rational numbers. Decimal numbers come in two varieties: repeating and non-repeating for the terminating and non-terminating numbers, respectively. Rational numbers are real numbers that repeat or terminate. For further information on rational numbers and their decimal expansions, have a look at some of the cases that have been solved and are provided in this article.