Are you excited to know how fractions are represented?
What role does a fraction bar play in a fraction?
Yes!
Here, we will discuss what fraction bar means and its different uses. But, before knowing about the fraction bar, let’s know what fractions are.
What Are Fractions?
A fraction is a number that represents the equal parts of a whole number. Let’s understand with an example:
Suppose you have one whole watermelon and if you cut it into two equal parts, it will be represented as 1/2.
Fractions
But, if you cut one whole watermelon into 4 equal parts, it will be represented as 1/4.
Parts of a Fraction
A fraction has two main parts known as numerator and denominator. The number written on the top of a line is called a numerator. On the other hand, the number written below the line is called a denominator.
(Image will be uploaded soon)
Meaning of Numerator and Denominator
The numerator means the total number of equal parts you have.
Contrarily, the term denominator means the total number of parts in a whole.
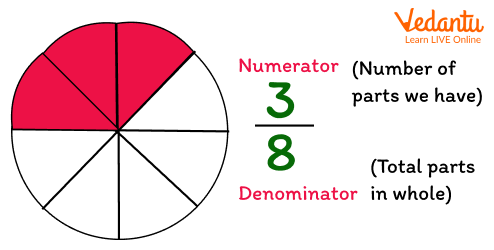
Numerator and Denominator
Now, let's know what a fraction bar means in a fraction.
What Does Fraction Bar Mean?
Fraction bar is nothing but a line that separates both numerator and denominator in a fraction.
Fraction bars are also known as “ Vinculum” in some countries.
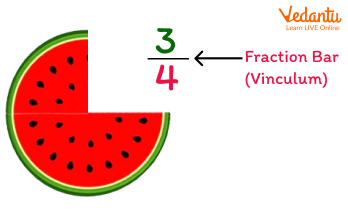
Fraction Bar
What Are Fraction Bar Models?
Fraction bars, also known as strips, are types of bar models. A fraction bar model is nothing but a drawing of a fraction using a rectangle. Below, you can see the fraction bar model for one whole, one half, one third, one fourth, one fifth, one sixth, one seventh, and one eight.
Fraction Bar Models
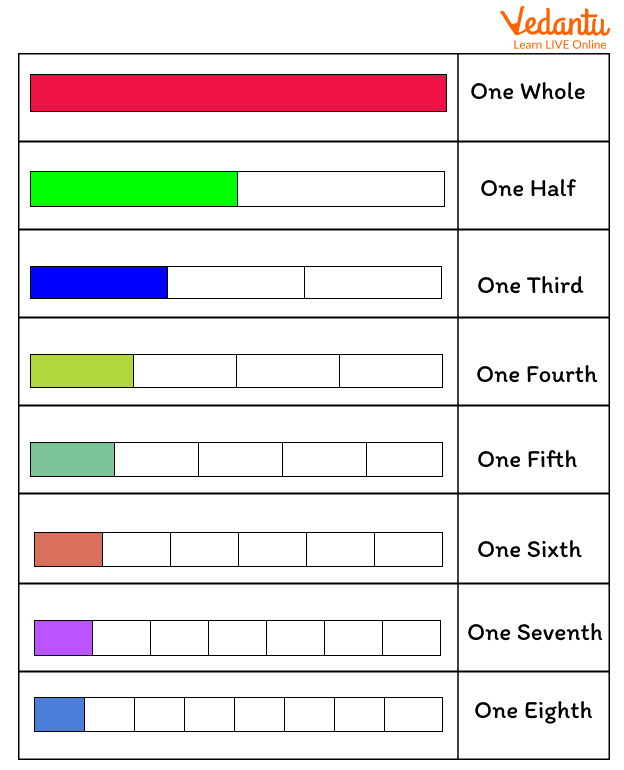
Fraction Bar Models
Fraction Bar Represents Division
Do you know the fraction bar indicates “division” in fraction.
Let’s see how!
Fraction bar is also represented as 1/12 or 1/2. The meaning of fraction bar is the same regardless of its representation. It separates both numerator and denominator in a division. Also, the fraction bar represents division in a fraction. In division, the fraction bar acts as a division symbol where the numerator is the dividend and denominator is the divisor.
Fraction Bar Represents Equality
Fraction bars are used to represent equality. Let’s learn how.
Two fraction bars with the same shaded amount represent two equal fractions. Look at the fraction bar below to understand it in a better way.
Fraction Bar Represents Equality
Fraction Bar Represents Inequality
Fraction bar also represents inequality. Let’s learn how.
If two fraction bars have different shaded amounts, the bar with the greater amount of shading is termed as greater fraction. Look at the fraction bar below to understand it in a better way.
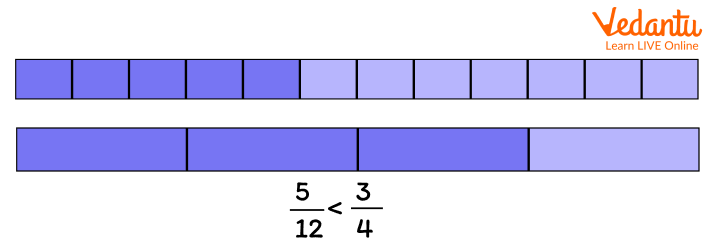
Fraction Bar Represents Inequality
Fraction Bar with Common Denominators
Two fraction bars with different numbers of parts have different denominators in their fraction. For example, the fraction bars of 1/2 and 1/3 have different numbers of parts and different denominators.
If we replace the fraction bars of 1/2 and 1/3 by fraction bars having the same or common number of parts, namely a 3/6 fraction bar and 2/6 fraction bar respectively, we will get a new denominator 6 as a common denominator for 1/2 and 1/3. Look at the fraction bars below to understand it in a better way.
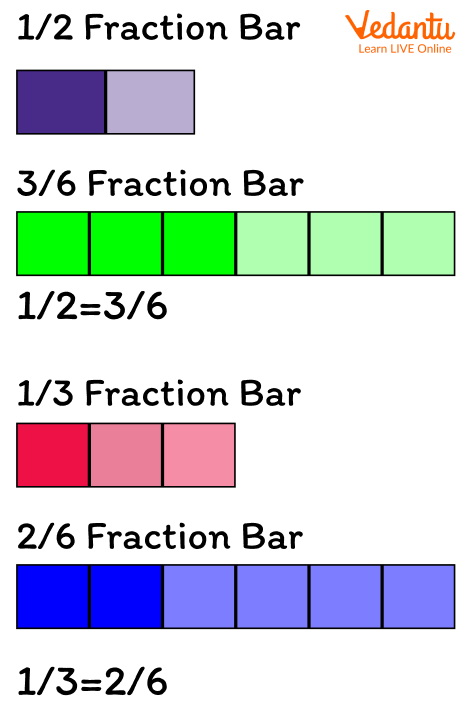
Fraction Bar with Common Denominators
Here, the new denominator ‘6’ is a common denominator for the fractions 1/2 and 1/3.
Fraction Bar Acts as a Grouping Symbol
Fraction bar also acts as a grouping symbol. The expression written above and below the fraction bar should be treated as if they are placed in parenthesis. For example, the expression $\frac{7+3}{5-3}$ means ( 7 + 3) (5 - 3). This order of operation tells us to simplify the numerator first, then the denominator, and then fraction. Let’s simplify it!
Step 1: Simplifying the numerator:
$\frac{7+3}{5-3}$ = $\frac{10}{5-3}$
Step 2: Simplifying the denominator:
$\frac{7+3}{5-3}$ = $\frac{10}{2}$
Step 3: Simplifying the fraction:
$\frac{10}{2}$ = 5
Did You Know?
The Arabs were the first to introduce the horizontal fraction bar. They first copied the Hindu notation but later on improved it by placing a horizontal bar between two numbers.
The diagonal fraction bar is also termed as solidus or virgule.
The horizontal line in a fraction is not termed a fraction bar if the numbers written on the top and bottom of the fraction bar are not integers. For example, \[ \frac{2.5}{4} \] → Not a Fraction Bar
FAQs on Fraction Bar - A line That Separates Top and Bottom Part of Fraction Bar
1. What are proper and improper fractions?
In the proper fraction, the value of the numerator is less than its denominator and represents the quantity less than the whole or < 1. Whereas, in improper fraction, the value of the numerator is more than its denominator and represents the quantity greater than the whole or > 1.
2. How do fraction bars help students to add fractions with different denominators?
To add or subtract fractions with different denominators, we rename the fractions with common denominators. Then add or subtract and simplify. For example, you want to add $\frac{1}{11} + \frac{2}{3}$. To add the given fraction, we will first find out the LCM of denominators. Here, the LCM of 11 and 3 is 33. Now, we will find the equivalent fraction which has 33 in the denominator. After finding equivalent fraction, we will multiply the numerator and denominator of 1/11 by 3 and 2/3 by 11 as shown below.
$\frac({1×3}{11×3}) + \frac({2×11}{3×11}) = \frac{3}{33} + \frac{22}{33}$
Now, since we have the same denominators, we will add the numerator and denominator individually as shown below.
$\\frac{3}{33} + \frac{22}{33} = $\\frac{25}{33}$
3. How fraction bars help students to divide fractions?
To divide fractions regardless of denominator, use the reciprocal of the second fraction i.e., divisor and change the division sign to a multiplication sign and multiply. For example:
$\\frac({1}{2} ÷ \frac{1}{6}) = \\frac{1}{2} × \\frac{6}{1}) = \frac{6}{2} = 3$
