




Introduction to H.C.F
H.C.F stands for Highest Common Factor. To find the H.C.F of two numbers we need to factorise the numbers and then take the common factors. After which we have to multiply the common factors and get the required H.C.F. In this article, you will get to know how to find HCF of two numbers, hcf of two numbers by division method and hcf of two numbers formula. To find the HCF by division method you will have to divide the larger number by the smaller number, until we get a remainder zero or unless further division is not possible.
H.C.F of Two Numbers
To find the HCF of any two numbers we need to follow the following steps:
Step 1: Take out the factors of the numbers. Let us suppose that the two numbers are 96 and 112.
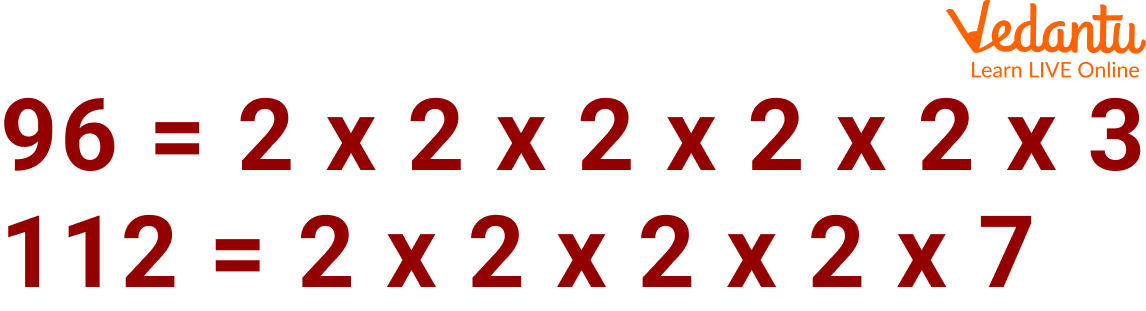
Carrying Out HCF of 96 and 112
Step 2: Now we need to look at the common factors (C.F) of the numbers as shown below.
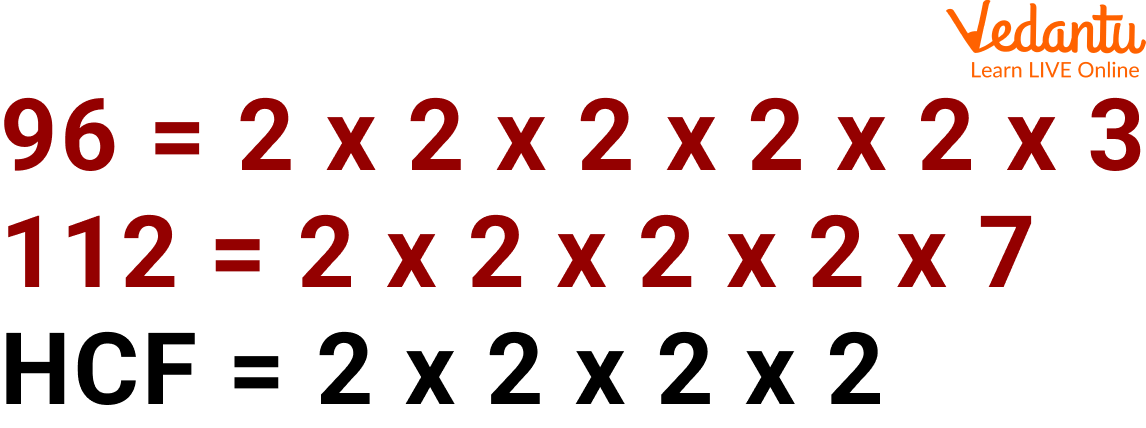
Carrying out HCF of 96 and 112
Step 3: We can see clearly the common factors highlighted in the colour blue. Now we will take the common factors from both the numbers and multiply them to get the HCF.
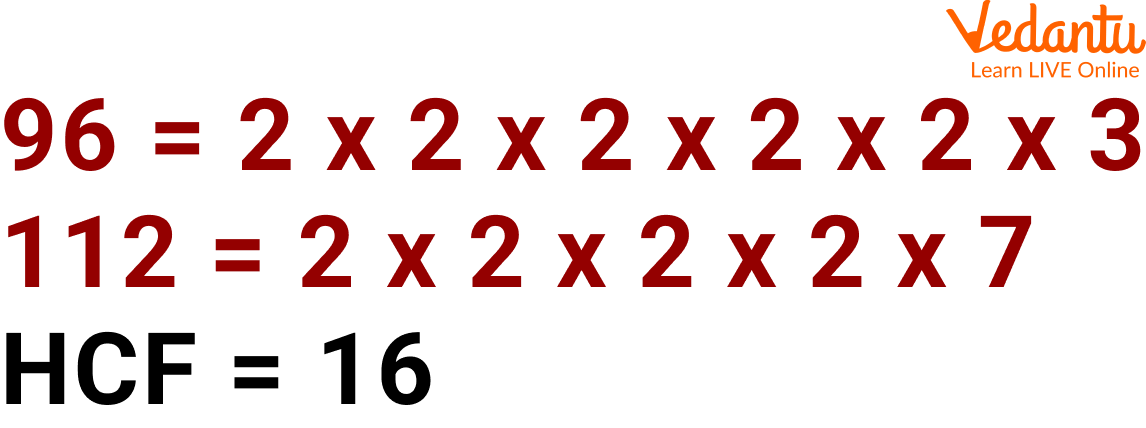
The HCF of 96 and 112 is 16
HCF of Two Numbers by Division Method
To find the HCF by division method you will have to divide the larger number by the smaller number and then again the remainder will become the divisor and divide the smaller number until we get a remainder zero or such that further division is not possible. Let’s practically understand this with the help of some examples.
Let us take two numbers, 46 and 242.
To find the HCF by division method we will divide the larger number by the smaller number.

HCF of 46 and 242
Hence, the required HCF of the numbers 46 and 242 is 2.
This method is also known as Euclid’s Division method named after the mathematician Euclid.
Let us consider a few more examples to understand the division method more clearly.
Solved Examples
Example 1: Find the H.C.F of 50 and 75.
Ans: First, you need to find the factors of the given numbers.

Step 1 of carrying out HCF of 50 and 75
After writing the factors then we will find the common factors. Here in this case the common factors are 5 and 5.

Step 2 of carrying out HCF of 50 and 75
After getting the common factors we will multiply the common factors to get the required H.C.F

HCF of 50 and 75 is 25
We can see clearly that the H.C.F of 50 and 75 is 25.
Example 2: Find the H.C.F of 432 and 876.
Ans: First, we need to find the factors of the given numbers.
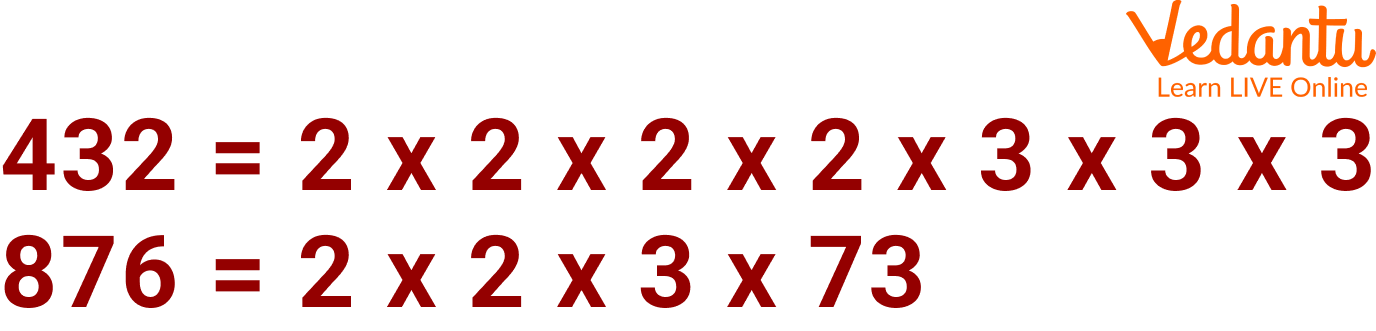
Step 1 of carrying out HCF of 432 and 876
Now taking out the common factors from the factors above. We can see that the common factors are 2, 2 and 3.
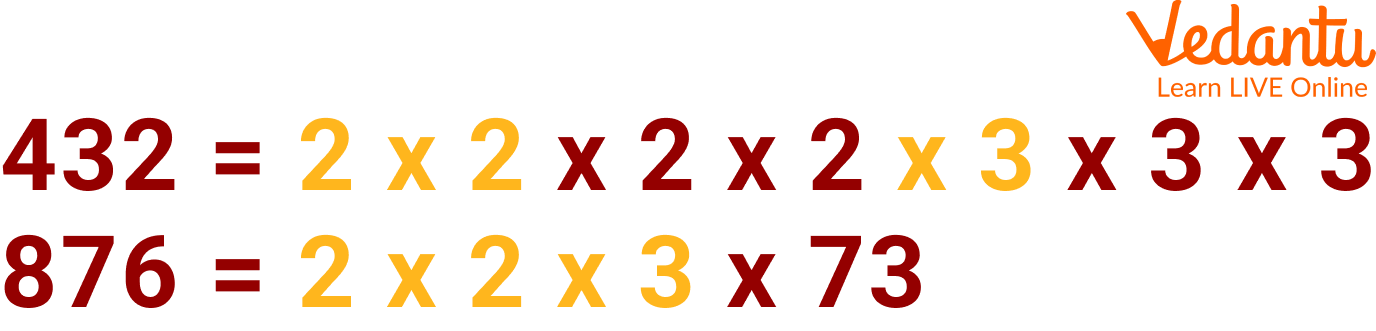
Step 2 of carrying out HCF of 432 and 876
Now after multiplying the common factors we will get the required H.C.F of the given numbers.
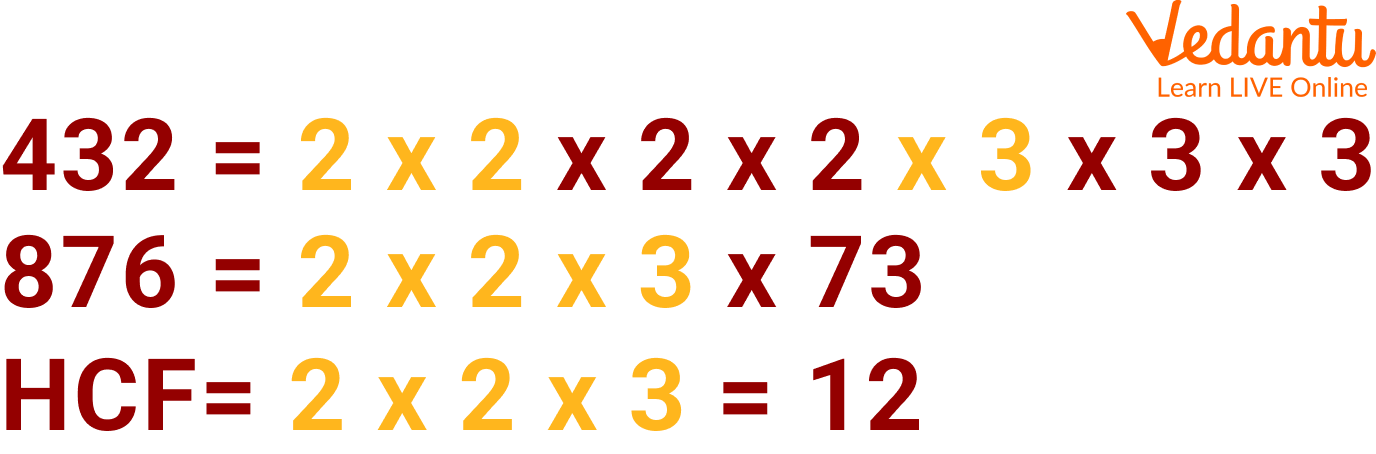
The HCF of 432 and 876 is 12
Hence, the required H.C.F of the given numbers is 12.
Example 3: Find the HCF of 1334 and 8948.
Ans: We can see that the smaller number is 1334 and the larger number is 8948 so we will divide 8948 by 1334.
Here the smallest number which divides the dividend is 2 so we can say that the HCF of the given numbers 1334 and 8948 is 2.
Example 4: What is the highest common factor of 96 and 404?
Ans: Prime factorization of 96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
Prime factorization of 404 = 2 × 2 × 101 = 22 × 101
HCF(96, 404) = 22 = 4
Therefore, the highest common factor of 96 and 404 is 4.
Practice Questions
Q 1 Find the H.C.F of 12, 45 and 75.
Ans: 3
Q 2 Find the H.C.F of 18,30 and 42.
Ans: 6
Q 3 Find the HCF of 867 and 255.
Ans: 51
Q 4 Find the HCF of 4052 and 12576.
Ans: 4
Summary
From HCF of two numbers examples, we have learnt to find the factors and then take the common factors. Then after that multiplication of the common factors will give us the HCF. We can use the division method to find the HCF. Hence, after going through this article we have made our concepts of HCF very clear in both methods and now we know how to find HCF of two numbers. With the examples and practice problem, we will get more clarity on the topic. So after reading the article go through the practice problem to have better understanding.
FAQs on HCF of Two Numbers
1. Where do we use HCF in real life?
It is used to split things into smaller sections, to arrange something into rows or groups, to distribute more numbers of items to large groups, and to figure out how many people we have to invite and so on when we want to split things into smaller sections.
2. What is the importance of using the highest common factors?
This method can be especially beneficial when finding prime factors or inverses because it makes it much easier to identify all prime factors and reciprocals on one line (in contrast with how reversing an equation plays out). H.C.F is mainly used in mathematical problems to split things into smaller sections.
3. What are the other names of H.C.F?
HCF is also known as Greatest Common Measure (GCM) and Greatest Common Divisor (GCD). The HCF or GCD of two numbers is the largest number that divides both of them without a remainder. The LCM or GCD measures how many numbers can be divided without a remainder by other numbers.











