How to Solve Fractions?

We often use fractions in our daily life. For example, we use fractions to measure the amount of food we consume, or to calculate the price of a product. Fractions are also used in mathematics and science, such as when measuring angles or calculating the area of a circle.

A fraction shows part of a whole. This whole can be a region or a collection. The word fraction is derived from the Latin word "fraction" which means 'to break'. For example, $\dfrac{3}{4}$ means three-fourths, or three parts out of four. The ratio of two numbers is expressed mathematically as a fraction. The numerator (top number) is called the dividend and the denominator (bottom number) is called the divisor. In this article, we will learn about how to solve fractions, and we will also see some fraction examples with answers.

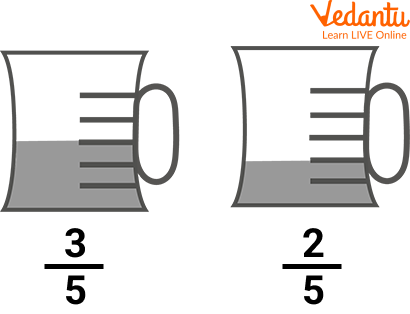
Quantity in Fractions

How to Add and Subtract Fractions?

Addition and subtraction of fractions is done using similar rules in which the denominators are checked before the addition or subtraction starts. After the denominators are checked, we can add or subtract the given fractions accordingly. The denominators are checked in the following way.

• If the denominators of the given fractions are the same, we add or subtract only the numerators and we retain the denominator.

• If the denominators are different, we convert the fractions to like fractions so that the denominators become the same, and then we add or subtract, whatever is required.

Adding and Subtracting Fractions with Like Denominators

The process for adding and subtracting fractions with denominators is quite simple because we just need to work with the numerators.

Let us add the fractions $\dfrac{1}{5}$ and $\dfrac{2}{5}$ using rectangular models. In this case, both the fractions have the same denominators. These fractions are called fractions.

In this case, we need to add $\dfrac{1}{5}$ + $\dfrac{2}{5}$. Let us use the following steps to understand the addition.

Step 1: Add the numerators of the given fractions. Here, the numerators are 1 and 2, so it will be 1 + 2 = 3

Step 2: Retain the same denominator. Here, the denominator is 5.

Step 3: Therefore, the sum of $\dfrac{1}{5}$ + $\dfrac{2}{5}$ = $\dfrac{1+2}{5}$ = $\dfrac{3}{5}$

Now, let us subtract the fractions with denominators in numerical terms. In this case, we need to subtract $\dfrac{2}{5}$ - $\dfrac{1}{5}$. Let us understand the procedure using the following steps.

Step 1: We will subtract the numerators of the given fractions. Here, the numerators are 2 and 1, so it will be 2 - 1 = 1

Step 2: Retain the same denominator. Here, the denominator is 5.

Step 3: Therefore, the difference of $\dfrac{2}{5}$ - $\dfrac{1}{5}$ = $\dfrac{2 - 1}{5}$ = $\dfrac{1}{5}$

Adding and Subtracting Fractions with Unlike Denominators

For adding and subtracting fractions with unlike denominators, we need to convert the unlike fractions to like fractions by writing their equivalent fractions in such a way that their denominators become the same.

Example: Add $\dfrac{1}{5} + \dfrac{1}{3}$

Ans: For adding unlike fractions, we need to use the following steps

Step 1: Find the denominators' Least Common Multiple (LCM). Here, the LCM of 5 and 3 is 15.

Step 2: Convert the given fractions to like fractions by writing the equivalent fractions for the respective fractions such that their denominators remain the same. Here, it will be $\dfrac{1}{5} \times \dfrac{3}{3}=\dfrac{3}{15}$

Step 3: Similarly, an equivalent fraction of $\dfrac{1}{3}$ with denominator 15 is $\dfrac{1}{3} \times \dfrac{5}{5}=\dfrac{5}{15}$

Step 4: Now that we have converted the given fractions to like fractions, we can add the numerators and retain the same denominator. This will be $\dfrac{3}{15}+\dfrac{5}{15}=\dfrac{8}{15}$.

For subtracting unlike fractions, we follow the same steps as we did for the addition of unlike fractions. Let us understand this with the help of an example.

Example: Subtract $\dfrac{5}{6} - \dfrac{1}{3}$

Ans: For subtracting unlike fractions, we need to use the following steps.

Step 1: Find the denominators' Least Common Multiple (LCM). Here, the LCM of 6 and 3 is 6 .

Step 2: Convert the given fractions to like fractions by writing the equivalent fractions for the respective fractions such that their denominators remain the same. Here, it will be $\dfrac{5}{6} \times \dfrac{1}{1}=\dfrac{5}{6}$

Step 3: Similarly, an equivalent fraction of $\dfrac{1}{3}$ with denominator 6 is $\dfrac{1}{3}$ $\times \dfrac{2}{2}=\dfrac{2}{6}$

Step 4: Now that we have converted the given fractions to like fractions, we can subtract the numerators and retain the same denominator. This will be $\dfrac{5}{6}-\dfrac{2}{6}=\dfrac{3}{6}$. This can be further reduced to $\dfrac{1}{2}$

Adding and Subtracting Fractions Related Examples

Here are a few examples related to adding and subtracting fractions examples, which can be solved and their concept can be improved further:

Q 1. Subtract the fractions $\dfrac{2}{5}$ and $\dfrac{1}{5}$.

Ans: The solution is as follows:

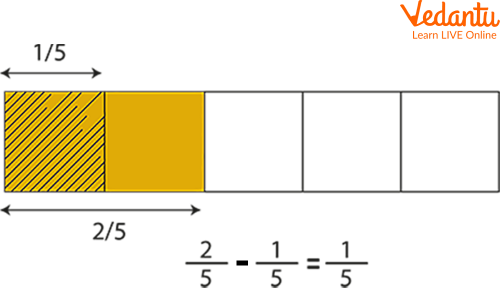
Subtraction of fractions

Q 2. Subtract the fractions $\dfrac{3}{4}$ and $\dfrac{2}{4}$.

Ans: The solution is as follows:

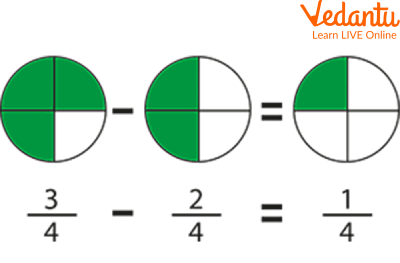
Subtraction of Fractions

Q 3. Find the sum of fractions $\dfrac{1}{7}$ and $\dfrac{4}{7}$.

Ans: The solution is as follows:

$\dfrac{1}{7}$ + $\dfrac{4}{7}$

Here, the denominator is the same.

Therefore, we will add the numerator to get the required result.

$=\dfrac{1}{7}$ + $\dfrac{4}{7}$

$=\dfrac{1+4}{7}$

$= \dfrac{5}{7}$

Q 4. Subtract $\dfrac{2}{3} - \dfrac{2}{5}$

Ans: The given fractions are unlike fractions. So, we need to find the LCM of the denominators, convert $\dfrac{2}{5}$ and $\dfrac{2}{3}$ to equivalent fractions of the same denominator, and then subtract.

$\operatorname{LCM}$ of $(3,5)=15$

$=\left(\dfrac{2}{3} \times \dfrac{5}{5}\right)-\left(\dfrac{2}{5} \times \dfrac{3}{3}\right)$

$=\dfrac{10}{15}-\dfrac{6}{15}$

$=\dfrac{4}{15}$

Therefore, the difference is $\dfrac{4}{15}$

Adding and Subtracting Fractions Related Worksheet

Here is a worksheet related to Adding and Subtracting Fractions, solve the fractions given below to revise the concepts:

Q 1. $\dfrac{1}{5}+\dfrac{3}{5}=$

Q 2. $\dfrac{4}{13}+\dfrac{7}{13}=$

Q 3. $\dfrac{5}{11}+\dfrac{2}{11}=$

Q 4. $\dfrac{6}{14}+\dfrac{3}{10}=$

Q 5. $\dfrac{3}{5}+\dfrac{2}{3}=$

Summary

In conclusion, fractions are a very important concept to learn. They are used in daily life, as well as in science and math. It is important to know that fractions can be represented by equivalent ratios, which can be simplified or decomposed. Fractions are important because they teach us how to work with numbers and fractions in order to solve problems.

When you are solving a fraction problem, you need to make sure that you have the right numbers in the numerator and denominator. If they don't match up, then it will not be possible to divide them. They are a part of the math curriculum and are taught to children from an early age. That's what we learned through this article, we also saw some worksheets and fraction sums with answers.