




Introduction to LCM - Least Common Multiple
"LCM" is an acronym for "least common multiple." The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of each. This is the mathematical definition of "Least Common Multiple (LCM)," and we will be exploring LCM definition and examples. Sometimes it's hard to tell what the LCM should be, but we've got your back! In this article, we'll show you how to find the LCM of 3 and 4.

Full Form of LCM.
What is Multiple?
Our main focus is on the LCM of 3 and 4 but before directly jumping on that we shall discuss; what is multiple?
The product of two given numbers is called a multiple. A multiple is gained by multiplying any number with other numbers like 1,2,3,4 etc.,
For example, the multiples of 2 are 2, 4, 6, 8, 10, 12,14, and so on…
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, and so on…
Now that you know what a multiple is, we shall move on to the next thing which is what is a common multiple. A common multiple is a number that is the common multiple of two or more numbers.
For example: The common multiple in the given numbers 2 and 3 is 6 and 12.
Through the above information, we have now idea about the LCM definition and examples.
What is the Definition of LCM?
The definition of LCM is given below:
Now that you know what a multiple is and what a common factor is, it's time to learn what is the least common multiple. The Least Common Multiple is the smallest number that two numbers will divide into. Hence, the LCM of two or more numbers is the smallest number that can exactly divide each of the given numbers.
Examples of LCM
LCM of 5 and 10 is 10.
LCM of 5 and 15 is 15.
LCM of 22 and 24 is 264.
How to Find Least Common Multiple of 3 and 4?
Let us find out the LCM of 3 and 4.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...... etc.
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, ...... etc.
If you look closer you will find a common multiple of 3 and 4 that is 12.
Let us have a look at the LCM of 2, 3, and 4.
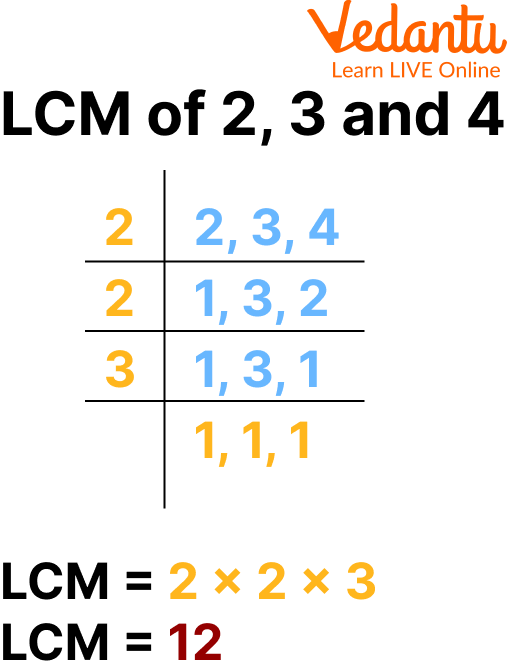
Representation of LCM
How to Find LCM Using Different Methods?
To make you understand better how to find out LCM using different strategies, let us take some LCM examples:
Solved Examples
Q 1. Find out the LCM of 8, 12, and 16 by the factorization method.
Ans: 8= 2x2x2
12= 2x2x3
16= 2x2x2x2
Therefore LCM OF 8, 12, 16 is;
2x2x2x2x3= 48
Q 2. Find out the LCM of 3, 4, and 6 by multiplication method.
Ans: Multiples of 3= 3, 6, 12, 15, 18, 21, 24
Multiples of 4= 4, 8, 12, 16, 20, 24, 28
Multiples of 6= 6, 12, 18, 24, 30, 36, 42
The common multiples of 3,4 and 6 are 12 and 24.
The Least Common multiple of 3, 4 and is 12.
Practice Problems
Q 1. Find the common multiple of 9 and 27.
Ans: 27
Q 2. Find the LCM of 16, 24, and 48 by finding common prime factors.
Ans: 48
Q 3. Find the LCM of 15 and 30 by the prime factorization method.
Ans: 30
Q 4. Find the LCM of 70 and 110 by the long division method.
Ans: 770
Summary
In this chapter, we learned about multiples, what are common multiples and what are least common multiples. LCM of a given number is the smallest number that two numbers will divide into. We also learned different methods to achieve the LCM of given numbers i.e, the prime factorization method, multiplication method, and long division method.
FAQs on Least Common Multiple (LCM)
1. What is Known as Multiples and Common Multiples?
Ans: A multiple is a result that is received by multiplying any number by an integer ( it should not be a function). We get the multiples of a whole number by taking out the product of any of the counting numbers and that of whole numbers.
For example, we can find out the multiples of 5 by multiplying the number 5 by 1, 5 by 2, 5 by 3, etc…
Common Multiples
The multiples that are common to two or more than two numbers are known as common multiples of those numbers.
For Example
Consider any two number 50 and 60
Multiples of 25 are = 25,50,75,100,125,150,175,200….
Multiples of 50 are - 50,100, 150, 200,250,300,50,400…
In the above example, we can see that 50,100, 150 and 200 are the first four common multiples of 25 and 50.
2. How to Find the LCM?
Ans: Two Methods to Find the LCM of Integers are Stated below:
By Finding the Multiples
By Prime Factorization.
By Finding the Multiples
In this method, the least common multiples can be found by writing down the multiples of individual numbers and then find the first common multiples between them. For example, there are two numbers 10 and 30. Then the multiples of 10 and 30 can be written as
Multiples of two digit number 10 = 10, 20, 30, 40, 50...
Multiples of two digit number 30 are -30 , 60, 90 ,120, 150 ….
The first common multiple or the least common multiple of both the numbers is 30. Hence the LCM of 10 and 30 is 30.
By Prime Factorization Method
The other method to find the least common multiple is the prime factorization method.
Let us take three numbers 12,16 and 24. The first step is to write the prime factors of all these three numbers individually.
12= 2*2*3
16= 2*2*2*2
24= 2*2*2*3
Now write the prime factors of all the three numbers togetherly,
12*16*24= 2*2*3* 2*2*2*2*2*2*2*3
Now, we will get the prime numbers by pairing the common prime factors,
Here, we can see there are four pairs of 2 and one pair of 3
So the LCM of 12 , 16 and 24 will be: 2*2*2*2*3 = 48
3. How many methods are there for LCM?
There are three methods by which you can find out the least common multiple of the given numbers. The three methods are; i. Factorization method (by listing the factors of the given numbers), ii. Multiplication method (by listing all the multiples of the given number), iii. Long Division method (by dividing two large values with the least common multiple). These different methods provide an easier approach to finding the LCM of given numbers. You can use any of the three methods to find the LCM of the given numbers.
4. Why is LCM used?
Least Common Multiple (LCM) is a method in Mathematics to find out the minimum/ least/ lowest common multiple between any two or more numbers. LCM is also used to solve problems in which two different amounts can be solved using the simple technique of finding LCM. The least common multiple is also helpful in finding the common multiples of any numbers given irrespective of their large and small values. Finding out LCM gives you more than just the least common multiple, but it also gives you the multiple and the common multiples of the given numbers.
5. The LCM of two numbers is what number that is divisible by both numbers.
The LCM of two numbers is the smallest number that is divisible by both numbers.











