




An Introduction to Parallel Lines
No matter how far in either direction they may be extended, parallel lines are ones that are equally spaced apart from one another and never cross. For instance, parallel lines are represented by a rectangle's opposite sides. In terms of geometry, parallel lines are two separate lines that never cross each other and are located in the same plane. They may be vertical or horizontal. In this article, we'll talk about lines that are parallel to one another and the corresponding theorem, along with lots of examples that have been resolved.
Parallel Lines
Parallel lines are two straight lines that do not intersect on the same plane. Parallel lines AB and CD are shown in figure (a). They are identified as AB and CD, and we state that AB is parallel to CD. PQ and RS are non-parallel lines because they intersect at point T in figure (b), where produced lines RS and PQ meet.

Parallel Lines
Equal numbers of arrowheads pointing in the same direction are used to denote parallel lines. As seen in the illustration below, several parallel sets of lines are identified by various numbers of arrowheads.
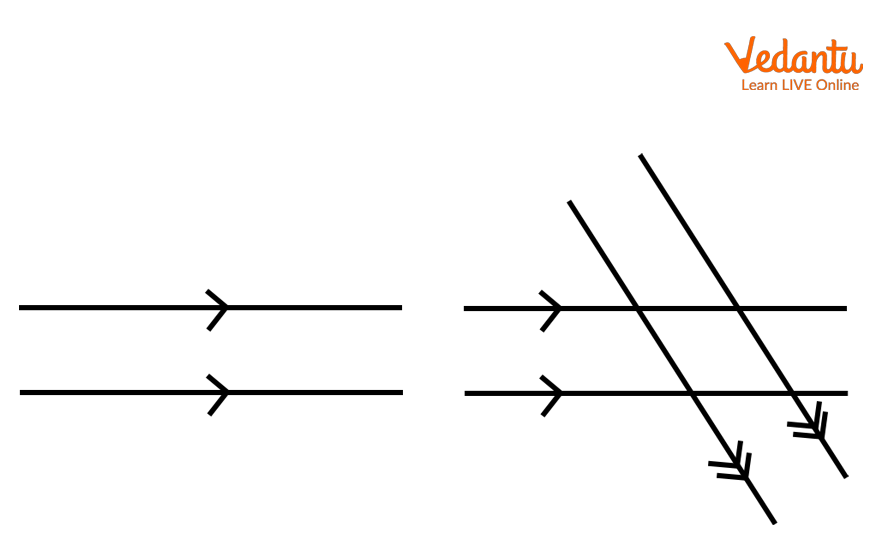
Parallel Lines with Similar Arrows
Construction of a Line Through a Point Outside a Given Line Parallel to It
Create the line XY and mark some point P on it. Use a ruler, and a pair of compasses, and just by using point P, draw a line AB that is parallel to XY.
Method:
Step 1. Mark a point P outside the given line XY and draw the line.
Step 2. Join points Q and P at another point Q on the XY axis.

Construction of Parallel Lines
Step 3. Consider any radius and Q as the centre, draw an arc that crosses XY at R and QP at S. Draw a seond arc considering P as the centre, and cut PQ at T, maintaining the same radius as before.
Step 4. Mark the point U on the aforementioned arc so that arc TU=arc SR, using T as the centre. Bring PU together and create it from both ends. Abbreviate this line as AB.
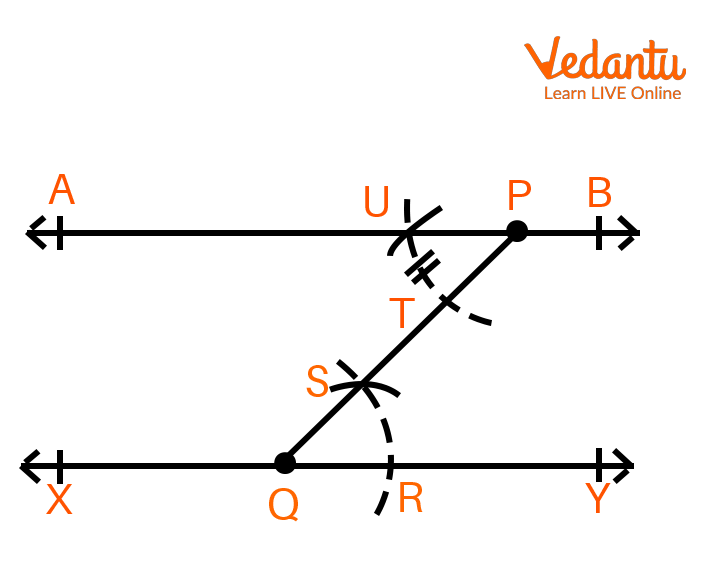
Parallel Lines
As a result, line AB is the line that is parallel to the specified line XY and passes through point P.
Transversal Lines
The term "transversal of those two lines" refers to a line that crosses two other lines. Eight angles are created at the two crossings in the image below, where TS is the transversal. Depending on how they relate to one another, these angles are named in pairs.

Transversal Lines
Properties of Transversal Lines
If a transversal cuts two parallel lines, then
The corresponding angles are equal.
The alternative angles are equal.
The transversal's internal angles on the same side add up to $180^\circ $.
Theorem - Lines Parallel to the Same Line
If we have been given two lines and both these lines are parallel to a third line, then according to this theorem, the two given lines will also be parallel to each other. Now, let's use the below figure to test how to prove two lines are parallel.

Lines Parallel to the Same Line
We can infer from the given figure that line m and line n are parallel to line l. Lines m $\parallel $ line l and line n $\parallel $ line l are examples. Additionally, the transversal for the lines l, m, and n is "t."
We can then state that $\angle 1$ Equals $\angle 2$ and $\angle 1 = \angle 3$. Using the axioms of related angles.
Therefore, we can also state that $\angle 2$ and $\angle 3$ correspond to one another and are equal to one another.
Thus, $\angle 2 = \angle 3$ .
Line m is parallel to line n, according to the converse of the corresponding angle axioms.
That is, Line m $\parallel $ Line n.
Note that this feature can be applied to several lines as well.
Solved Examples
Q.1. Indicate which of the following pairs of lines or rays appears to be parallel or intersecting.
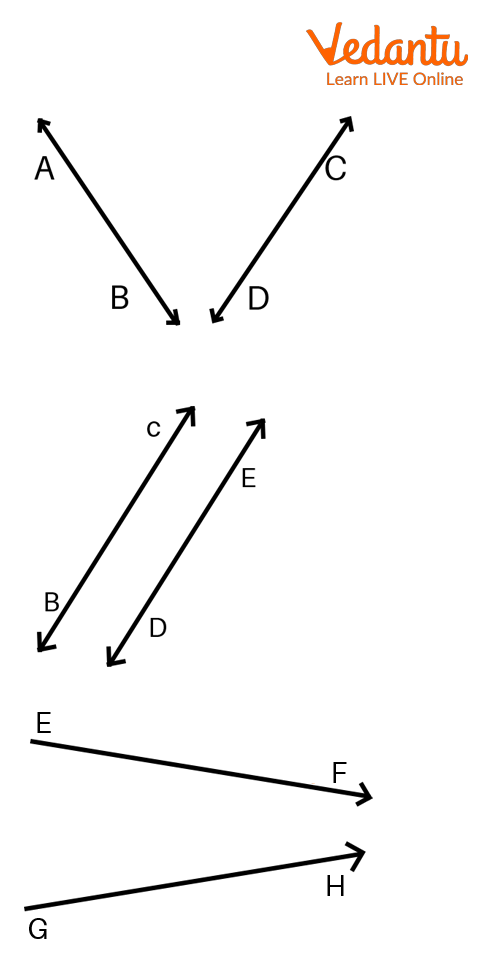
Parallel Lines and Transversal Lines
Solution: Two lines are intersecting if, when extended on either side, they cross or appear to cross; otherwise, they are parallel. Consequently,
Intersecting lines: The first pair of lines are intersecting lines because if both lines are extended then, they will surely meet at some point.
Parallel lines: The second pair is parallel lines as they will never cross each other even on extending on either of the sides.
Intersecting Lines: The third pair is also a pair of intersecting lines if we produce these lines they will intersect each other at some point for sure.
Q.2. Write down all pairs of parallel lines from the figure below.

Parallel and Transversal Lines
Solution: Regardless of how far apart they are in either direction, two straight lines that are located in the same plane are considered to be parallel if they do not cross or overlap.
$EF\parallel GH$, $EF\parallel IJ$, and $GH\parallel IJ$ are the parallel lines as a result.
Q.3. In the diagram below, $AB\parallel CD$, $CD\parallel EF$, and $EA \bot AB$. Find $x$, $y$ and $z$ values if $\angle BEF = 55^\circ $ .
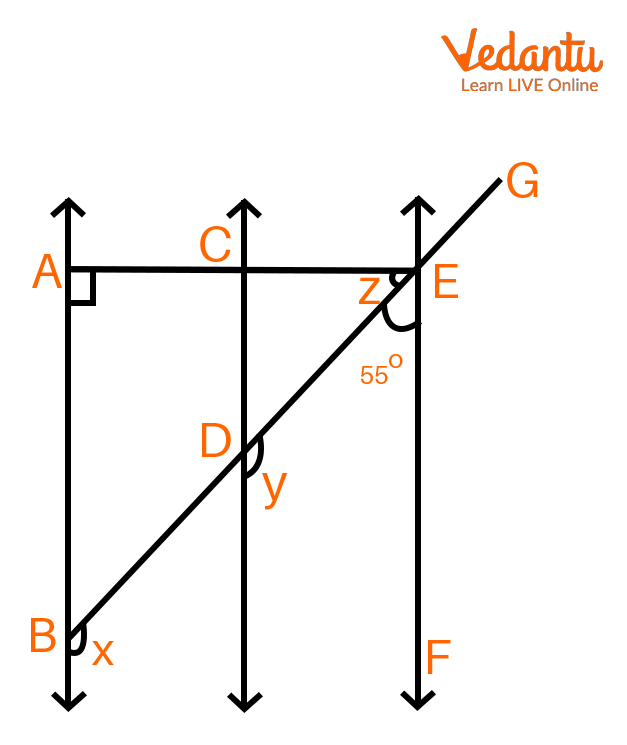
Parallel Lines and Transversal Lines
Solution: As a result of $CD\parallel EF$, $\angle y + 55^\circ = 180^\circ $ (sum of co-interior angles is supplementary).
\[\angle y = 180^\circ -55^\circ = 125^\circ \]
As a result of \[AB\parallel CD\] , $x$ equals $y$. (Corresponding angles are equal)
Thus, \[\angle x = 125^\circ \] .
Therefore, $AB\parallel EF$ because \[AB\parallel CD\] and $CD\parallel EF$ .
Therefore, \[\angle EAB + \angle FEA = 180^\circ \] (Sum of co-interior angles are supplementary)
Thus, \[90^\circ + \angle z + 55^\circ = 180^\circ \] , \[\angle z + 145^\circ = 180^\circ \] . Hence, $\angle z = 35^\circ $ .
As a result, the values of \[x = 125^\circ \] , \[y = 125^\circ \] and $\angle z = 35^\circ $ .
Practice Questions
Q1. In the following figure, if \[y = 130^\circ \] and AB line parallel to CD, calculate the value of $x$ .

Parallel Lines AB and CD
Q2. Calculate angle ABC if PQ $\parallel $ RS.

Parallel Lines PQ and RS
Answers
$30^\circ $
$110^\circ $
Summary
In this article, we first discussed parallel lines and how they are made, then transversals and the angle that the transversal creates when it cuts parallel lines. In addition, we studied the characteristics of parallel lines when crossed by a transversal. The proof regarding the parallel lines to the same line was then given. In addition, we worked through various instances to further our understanding of the idea.
FAQs on Lines Parallel to the Same Line
1. Do parallel lines intersect at infinity?
No, the definition itself states that parallel lines never cross. Parallel lines would therefore not intersect even at infinity.
2. When two lines cross one another, what happens?
Parallel lines lie on the same plane and never cross over (intersect), intersect, or come together. Let's say we have the following three lines: x, y, and z. Lines x and y are parallel to one another, with x parallel to z and y parallel to z. Therefore, it is simple to state that x and y are parallel to one another. Therefore, two lines are said to be parallel to one another if they are parallel to the same line.
3. How can you verify that the lines are parallel?
The corresponding angles must be equal, the alternate angles must be equal, or the co-interior angles must be supplementary in order to show that the given lines are parallel.





















