Mixed Fraction Subtraction

What are Fractions?

Like fractions are two or more fractions with the same denominator. Another way to represent an improper fraction made up of a whole number, and a proper fraction is with mixed fractions. The subtraction operation between any two mixed fractions is known as subtracting mixed fractions. This article will examine various approaches and regulations to comprehending subtracting mixed fractions. The same procedures as subtracting mixed fractions with like denominators can be used for, unlike denominators by first converting them to like denominators using the LCM.

What are Mixed Fractions?

A mixed fraction, sometimes referred to as a mixed number, combines a whole number with a fraction. The fraction appears after the whole number to the right. Mixed fraction examples include the integers \[1\dfrac{1}{2}\] and \[33\dfrac{1}{3}\]. Both mixed fraction addition and subtraction are possible. Here we will learn about how to subtract mixed fractions.

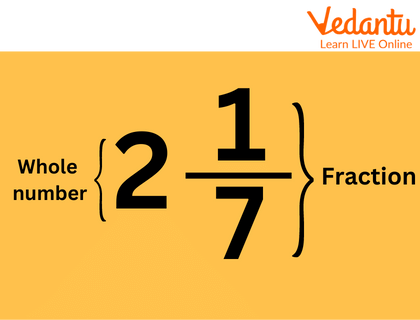
Mixed Fraction Example

How to Subtract Mixed Fractions with Whole Numbers

Case I: Subtracting Mixed Fractions Having Like terms

• Fractions are two or more fractions with the same denominator. As a result, mixed fractions with denominators, such as \[3\dfrac{2}{7}\], will have the same denominator as \[2\dfrac{1}{7}\]. Consider the following considerations when you're subtracting mixed fractions.

• A mixed number \[a\dfrac{b}{c}\] can be expressed as \[a + \left[ {\dfrac{b}{c}} \right]\]

• An improper fraction is created by multiplying a mixed number by its denominator, keeping the denominator, and adding the resulting number to the appropriate fraction's numerator.

• For instance, to change\[1\dfrac{6}{{11}}\]

We multiply 1 by 11 \[\left[ {1 \times 11 = 11} \right)\] and add it to 6 [\[11 + 6 = 17\]]. Therefore, 17/11 is the improper fraction.

• We shall divide the improper fraction's numerator by its denominator to transform it into a mixed number. The denominator stays the same, the remainder becomes the correct fraction's numerator, and the quotient becomes the whole number portion. For instance, to turn \[\dfrac{{22}}{3}\] into a mixed number, we must first divide 22 by 3, yielding a result of 7 and a remainder of 1. Thus, \[7\dfrac{1}{3}\] is the mixed fraction.

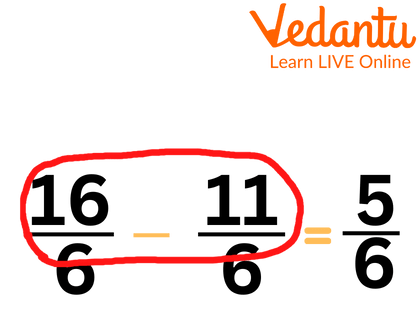
Subtraction Of Like terms

Case II: Subtracting mixed fractions having unlike terms

Unlike fractions are those that have different denominators. Thus, \[5\dfrac{1}{3}{\rm{ and }}3\dfrac{2}{5}\] are two examples of mixed fractions with dissimilar denominators. To understand the processes for subtracting mixed fractions with dissimilar denominators, let's use an example.

There are two options on how to subtract.

Method I: Subtracting fractions and whole integers separately by bringing their denominators to the same value

Method II: It involves turning Mixed Fractions into improper fractions, then subtracting them by setting their denominators to the same value.

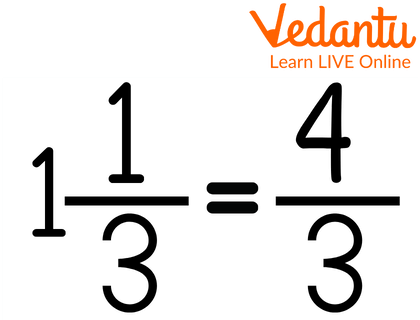
Conversion of Mixed fraction to Improper Fraction

Conclusion

Using mixed fractions is another way to represent an improper fraction made up of a whole integer and a proper fraction. Subtracting mixed fractions is the process of taking away any two mixed fractions. The procedure of removing any two mixed fractions is referred to as subtracting mixed fractions.

Solved Examples

Example 1: Subtract \[20\dfrac{2}{3}\] from \[15\dfrac{1}{3}\]

Ans: To answer this question, we'll apply the idea of subtracting mixed fractions. Given mixed fractions with the same denominator are \[15\dfrac{1}{3}\] and \[20\dfrac{2}{3}\] . We must solve\[20\dfrac{2}{3}\] \[ - \]\[15\dfrac{1}{3}\].

The whole numbers and the fractional parts will be subtracted separately and then combined as indicated below.

\[\begin{array}{l} = [20 - 15] + \left[ {\left[ {\dfrac{2}{3}} \right] - \left[ {\dfrac{1}{3}} \right)} \right]\\ = 5 + \dfrac{1}{3}\\ = 5\dfrac{1}{3}\end{array}\] 

Thus, \[20\dfrac{2}{3}\] \[ - \]\[15\dfrac{1}{3}\]=\[\;5\dfrac{1}{3}\].

Example 2: Sam has a 16-meter-long cloth. In order to make curtains for the house, he took \[13\dfrac{1}{4}\] m of fabric from it. How much fabric is still on him for future use?

Ans: If Sam had 16m long fabric with him and he took \[13\dfrac{1}{4}\]m of fabric away. Then he will have \[16 - 13\dfrac{1}{4}\] m of clothes with him.

\[\begin{array}{l}16 - 13\dfrac{1}{4}\\ = \dfrac{{16}}{1} - \dfrac{{53}}{4}\\{\rm{Taking LCM and solving:}}\\ = \dfrac{{84}}{4} - \dfrac{{53}}{4}\\ = \dfrac{{84 - 53}}{4}\\ = \dfrac{{31}}{4}\end{array}\] 

Thus, he will have \[\dfrac{{31}}{4}\] m of cloth with him.

Example 3: When subtracting mixed fractions, how do you borrow?

Ans: When subtracting mixed fractions, the whole number will lend to the proper fraction to increase it if the proper fractional part of the mixed fraction from which the other mixed fraction is being subtracted is less. For instance, to carry out

\[3\dfrac{1}{3} - 1\dfrac{2}{3}\]

\[\dfrac{1}{3} > \dfrac{2}{3}\], as can be seen. As a result, 1/3 will take 1 full from 3. 3/3 can be used to represent a whole. After subtracting one, the full number 3 becomes 2, and the fraction 1/3 becomes\[\left( {\dfrac{1}{3}} \right] + \left[ {\dfrac{3}{3}} \right) = \dfrac{4}{3}\]. Consequently, upon borrowing, the resulting modified mixed fraction is

\[2\dfrac{4}{3}\]

The subsequent subtraction will be

\[\begin{array}{l}2\dfrac{4}{3} - 1\dfrac{2}{3}\\ = 1\dfrac{2}{3}\end{array}\]