Pentagonal Pyramid Formula for Surface Area Volume and Solved Examples
What Is A Pentagonal Pyramid?
In Geometry, a pentagonal pyramid is a pyramid with a pentagonal base and five triangular faces that meet at a point known as the apex. The regular pentagonal pyramid has a base that is pentagonal in shape and lateral faces that are equilateral triangles. It is one of the Johnsons solid.
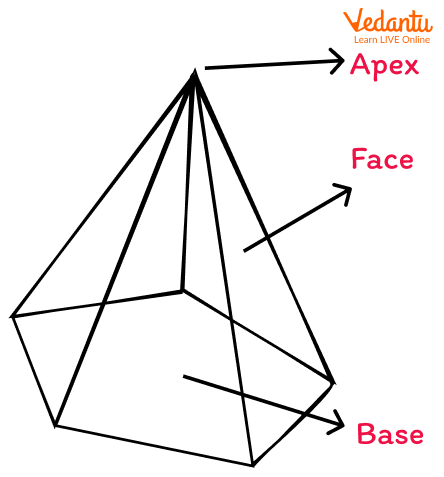
Pentagonal Pyramid
What are the Properties of a Pentagonal Pyramid?
The following are the properties of a pentagonal pyramid.
It has 6 faces.
The five side faces are triangular in shape.
The base is a pentagon.
It has 6 vertices.
It has 10 edges.
A pentagonal pyramid can also have an isosceles triangle (Triangle with two sides of equal length) as its lateral sides or lateral faces.
What is the Volume of the Pentagonal Pyramid?
The volume of a pentagonal pyramid is defined as the total space occupied by the pyramid in the three-dimensional space. The volume of a pentagonal pyramid is measured in cubic units.
The volume of any pyramid is calculated by multiplying the area of its base by its height and dividing the product by 3. Therefore, the volume of pyramid is given as,
Volume: 13 Base Area Height
As pentagonal pyramid has pentagonal base, therefore, the area of pentagon is calculated as:
Area = 1.72l²
Here, l is the length of one side of a pentagon.
The above formula for the area of the pentagon is calculated by dividing the pentagon into 5 triangles and finding the area of each triangle separately.
Therefore, the volume of pentagonal pyramid using the above expression for the area of given pentagon is calculated as:
Volume =1.72 3l²h
Here, l is the length of the one side of a pentagonal base and h is the height of the pyramid.
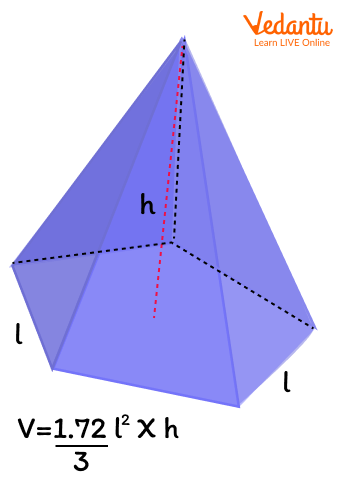
Volume of pentagonal pyramid
Let us understand the volume of the pentagonal pyramid with an example.
Example:
Find the volume of the pyramid with a pentagonal base 1 m and height 3 m.
Solution:
Pentagonal base : 1 m
Height of pentagon: 3 m
Now, we will use the volume of pentagonal pyramid formula with these values:
V = 1.72 31² 3
V = 1.72 3 3
V = 1.72
Hence, the volume of pentagonal pyramid with base length (1 m) and height (3 m) is given as 1.72m³.
What is the Surface Area of the Pentagonal Pyramid?
The surface area of a pentagonal pyramid is the entire surface occupied by the pyramid in three-dimensional space. The surface area of a pentagonal pyramid is measured in square units.
The surface area of any pyramid is calculated by adding the area of all the faces of the pyramid. Pentagonal pyramid has one pentagonal base and 5 triangular faces, and we used the following formula to calculate the area of the pentagonal face.
Area = 1.72l²
Here, l is the length of one side of the pentagonal base.
On the other hand, the area of triangle faces of pyramid is calculated by using the formula for area of triangle:
A = 12 Base Height
The five triangular faces of the pentagonal pyramid are congruent ( Congruent triangles have the same shape and same size).. Accordingly, the surface area of pentagonal pyramid is calculated as:
Surface Area of Pentagonal Pyramid Formula (AS) : 1.72l² + 52bh
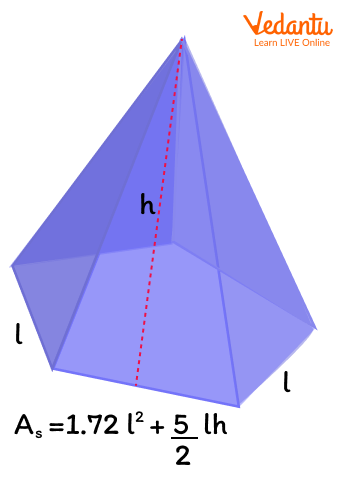
Surface area of pentagonal pyramid
Let us understand with an example.
Example:
Find the surface area of a pentagonal pyramid with height 5 m and side length 1 m?
Solution:
Height = 5 m
Length = 1 m
Now, we will use these values in the surface area of pentagonal pyramid formula:
(AS) : 1.72l² + 52bh
(AS) : 1.72(1)² + 52(1)(5)
(AS) : 1.72(1)² + 12.5
(AS): 14.22
Therefore, the surface area of the pentagonal pyramid is equal to 14.22 m².
In short, a three-dimensional shape with a pentagonal base and five triangular faces meeting is termed the pentagonal pyramid. As you have understood what a pentagonal pyramid is. Now, you can easily solve and practice sums based on the volume and surface area of the pentagonal pyramid using the formula discussed above.
FAQs on Pentagonal Pyramid Shape Definition and Properties
1. What is a pentagonal pyramid in geometry?
A pentagonal pyramid is a three-dimensional solid with a pentagon as its base and five triangular faces that meet at a single point called the apex.
- It has 1 pentagonal base.
- 5 triangular lateral faces.
- 1 vertex at the top (apex).
2. How many faces, edges, and vertices does a pentagonal pyramid have?
A pentagonal pyramid has 6 faces, 10 edges, and 6 vertices.
- Faces: 1 pentagonal base + 5 triangular faces = 6
- Edges: 5 base edges + 5 lateral edges = 10
- Vertices: 5 base vertices + 1 apex = 6
3. What is the formula for the volume of a pentagonal pyramid?
The volume of a pentagonal pyramid is V = (1/3) × Base Area × Height.
- First find the area of the pentagonal base.
- Multiply it by the vertical height.
- Divide the result by 3.
4. What is the surface area of a pentagonal pyramid?
The surface area of a pentagonal pyramid is the sum of the base area and the areas of the 5 triangular faces.
- Total Surface Area = Base Area + Lateral Area
- Lateral Area = (1/2) × Perimeter of base × Slant height
5. How do you find the base area of a regular pentagonal pyramid?
The base area of a regular pentagonal pyramid is found using the formula A = (5/4)s² cot(π/5), where s is the side length.
- This applies when the base is a regular pentagon.
- Alternatively, divide the pentagon into 5 congruent triangles and find their total area.
6. What is the difference between a regular and irregular pentagonal pyramid?
A regular pentagonal pyramid has a regular pentagon base and equal triangular faces, while an irregular one does not.
- Regular: All base sides equal, apex directly above center.
- Irregular: Base sides or triangular faces may differ.
7. What is the slant height of a pentagonal pyramid?
The slant height of a pentagonal pyramid is the distance from the apex to the midpoint of a base edge along a triangular face.
- It is used to calculate lateral surface area.
- In a regular pyramid, it can be found using the Pythagorean theorem: l² = h² + a², where h is vertical height and a is the apothem of the base.
8. How do you calculate the lateral surface area of a pentagonal pyramid?
The lateral surface area is calculated using L = (1/2) × Perimeter × Slant Height.
- Find the perimeter of the pentagonal base.
- Multiply by the slant height.
- Divide by 2.
9. Can you give a real-life example of a pentagonal pyramid?
A real-life example of a pentagonal pyramid is certain architectural roof designs shaped with a five-sided base.
- Some monuments and decorative structures use pentagonal pyramid shapes.
- It is studied in geometry, engineering, and design.
10. How is a pentagonal pyramid different from a pentagonal prism?
A pentagonal pyramid has one pentagonal base and an apex, while a pentagonal prism has two parallel pentagonal bases.
- Pyramid: 6 faces, 1 base, triangular sides.
- Prism: 7 faces, 2 bases, rectangular sides.
