Percentage of a Number - Calculation with Examples

The topic ‘Percentage’ is a very important concept because students use it regularly in various mathematical activities and day-to-day activities. So, it is essential to build the concept of percentage as future Maths concepts build upon prior knowledge. Learning the concept of percentage starts in third grade. It plays a crucial role throughout your life while solving mathematical problems.

So, in this article, we will discuss the definition of percentage, examples of percentage, and how to calculate it.

Let’s start with the definition of percentage.

What is Percentage?

A percentage in Mathematics is a number or ratio that is represented as a fraction of 100. The word ‘percent’ is derived from the Latin word ‘per centum’ which means “by a hundred”. Percentage is denoted by the symbol ‘%’. It is a dimensionless number and has no units.

Examples of Percentages

Percentage basically means a part per hundred. It can be expressed in fraction form as well as decimal form.

For example, if we say 25%, it means 25 out of 100. So, 25% is equivalent to the fraction 25/100 or 0.4 in decimal form.

Here are some examples of percentages.

• 10% is equivalent to 10/100 or 0.1

• 20% is equivalent to 20/100 or 0.2

• 25% is equivalent to 25/100 or 0.25

• 50% is equivalent to 50/100 or 0.5

• 75% is equivalent to 75/100 or 0.75

• 90% is equivalent to 90/100 or 0.9

• 100% is equivalent to 100/100 or 1

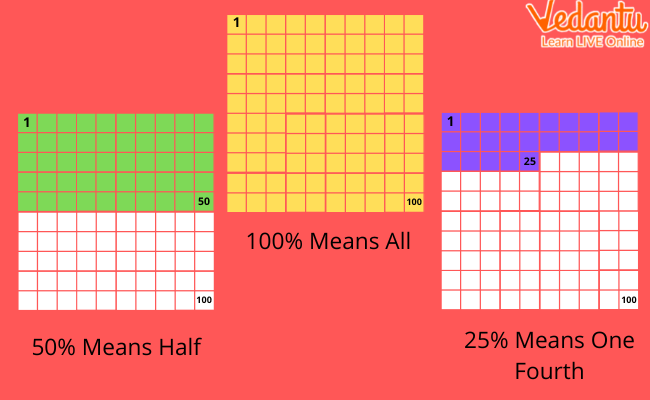
Examples of Percentage

Percentage Formula

To find out the share of a whole in terms of 100, we use the percentage formula. You can express a number as a fraction of 100 by using the percentage formula.

First, divide the value by the total value and then multiply it by 100 to get the percentage.

Percentage formula = (Value/Total value) × 100

For example, 4/5 × 100 = 0.8 × 100 = 80%

How to Calculate Percentage?

Follow the below steps to calculate the percentage of a number.

• To find out the percentage of a number if the given number is in the decimal form, you have to multiply the decimal number by 100. 

For example, to convert 0.6 to a percentage, you need to multiply 0.6 by 100. So, we will get 0.6 × 100 = 60%.

• To find out the percentage of a number if the given number is in fractional form, first, you have to convert it to a decimal form and then multiply it by 100.

For example, to convert 1/4 to percentage, first you need to convert 1/4 to the decimal form that is 0.25 and then multiply 0.25 by 100. So, we get 0.25 × 100 = 25%.

Solved Examples

1. Convert 0.32 to percentage.

Solution: Multiplying 0.32 by 100, we get 0.32 × 100 = 32% as the answer.

2. Convert the fraction 23/25 to percentage.

Solution: Converting 23/25 to a decimal value, we get 0.92. 

So, 0.92 × 100 = 92% is the answer. 

3. Convert 75% to a decimal value.

Solution: 75% means 75 out of 100. So, we can write it as 75/100. 

By simplifying this fraction, we get 3/4. 

Then, converting 3/4 to a decimal value, we get 0.75.

4. Convert 2.5% to fractional form.

Solution: 2.5% means 2.5 out of 100. So, we can write it in the fraction form as 

2.5/100. 

By simplifying the fraction, we get 1/40.

5. Find the value: 7.5% of 500.

Solution: 

=(7.5/100) × 500

= (3750)/100

= 37.5

6. The number 450 is what percentage of 1200?

Solution: 

=(450/1200) × 100

By simplifying the fraction, we get

= (3/8) × 100 

= 0.375 × 100

= 37.5%

So, the number 450 is 37.5% of 1200.

Conclusion

Possessing knowledge of how to calculate percentages is not only helpful for you to excel in Mathematics but also to apply outside the class and solve practical problems involving percentages. This article provides a step-by-step guide on how to calculate percentages with examples.