Ptolemy Theorem: Brief Introduction
Ptolemy Theorem is an important component of Euclidean Geometry. It is named after the Greek Mathematician and astronomer Ptolemy. The theorem is derived by him while applying to astronomy to supplement his table of chords and trigonometry for astronomy. In this article, we will discuss the Ptolemy’s theorem proof and Ptolemy’s theorem applications. Some Ptolemy's theorem examples will also be discussed for a better understanding of the topic. The theorem is mainly focused on the concept of cyclic quadrilaterals, so knowledge of cyclic quadrilaterals is essential for a better understanding of the theorem.
Table of Contents
Ptolemy Theorem: Brief introduction
History of Claudius Ptolemy
Statement of Ptolemy Theorem
Proof of Ptolemy Theorem
Limitations of the Ptolemy Theorem
Applications of the Ptolemy Theorem
Solved Examples
Important Formulas to Remember
Important Points to Remember
History of Claudius Ptolemy
Claudius Ptolemy
Image Credit: Wikimedia
Name: Claudius Ptolemy
Born: 100 AD
Died: 170 AD
Field: Mathematics and Astronomy
Nationality: Roman
Statement of Ptolemy Theorem
Ptolemy Theorem states that when a quadrilateral is inscribed in a circle, then the product of diagonals of the quadrilateral is equal to the sum of the product of pairs of opposite sides.
Proof of Ptolemy Theorem
Ptolemy's Theorem
Let us consider $A B C D$ a cyclic quadrilateral.
Now we can see that the chord $B C$, the inscribed angles $\angle B A C=\ angle B D C$, and on $A B, \angle A D B=\angle A C B$.
Now, Construct $K$ on $A C$ such that $\angle A B K=\angle C B D$.
(Note that: $\angle A B K+\angle C B K=\angle A B C=\angle C B D+\angle A B D \Rightarrow \angle C B K=\angle A B D .$ )
Now, by common angles property,
$\triangle K B C \sim \triangle A B D$
Similarly,
$\triangle A B K$ is similar to $\triangle D B C$.
Thus, $\dfrac{|A K|}{|A B|}=\dfrac{|D C|}{|D B|} and \dfrac{|K C|}{|B C|}=\dfrac{|A D|}{|B D|}$ due to the similarities noted above:
{$\triangle A B K \sim \triangle D B C and \triangle K B C \sim \triangle A B D$}
So $|A K| \cdot|D B|=|A B| \cdot|D C|$, and $|K C| \cdot|B D|=|B C| \cdot|A D|$
Adding,
$\Rightarrow|A K| \cdot|D B|+|K C| \cdot|B D|=|A B| \cdot|D C|+|B C| \cdot|A D|$
Equivalently, $(|A K|+|K C|) \cdot|B D|=|A B| \cdot|C D|+|B C| \cdot|A D|$
But
$\Rightarrow|A K|+|K C|=|A C|$
So,
$\Rightarrow|A C| \cdot|B D|=|A B| \cdot|C D|+|B C| \cdot|D A|$
Hence Proved.
Limitations of the Ptolemy Theorem
It is only applicable in the case of cyclic quadrilaterals.
It only tells us about the sides and diagonal length relationship and doesn’t give any idea about the angles of the quadrilateral.
Applications of the Ptolemy Theorem
Ptolemy's Theorem has a wide range of applications in astronomy. The discovery of the theorem is done for astronomy itself.
It is used to find the value of sides or diagonals of cyclic quadrilateral using the formula stated in the theorem.
It can be used to derive the Pythagoras theorem.
Solved Examples
1. In the given figure, $A B=10 \mathrm{~cm}, D C=5 \mathrm{~cm}, B C=20 \mathrm{~cm}, A D=15 \mathrm{~cm}$ and $A C=25 \mathrm{~cm}$, then find $D B$.
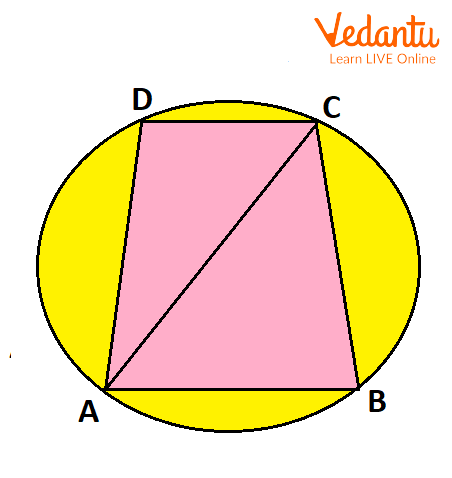
ABCD is a Cyclic Quadrilateral
Ans: By Ptolemy's Theorem, we have,
$D B \times A C=A B \times D C+A D \times B C$
Putting values, we get,
$\Rightarrow D B \times 25=10 \times 5+15 \times 20 $
$\Rightarrow 25 D B=50+300$
$25 D B=350$
$D B=\dfrac{70}{5}$
$D B=14 \mathrm{~cm}$
2. In the given figure, $A B=30 \mathrm{~cm}, D C=5 \mathrm{~cm}, B C=20 \mathrm{~cm}, A D=25 \mathrm{~cm}$ and $A C=25 \mathrm{~cm}$, then find $D B$.
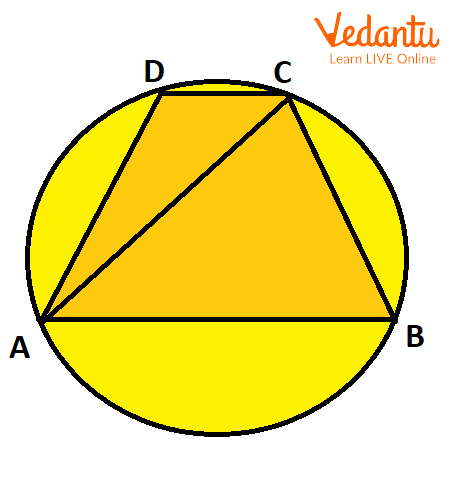
Cyclic Quad ABCD
Ans: By Ptolemy's Theorem, we have,
$D B \times A C=A B \times D C+A D \times B C$
Putting values, we get,
$\Rightarrow D B \times 25=30 \times 5+25 \times 20 $
$\Rightarrow 25 D B=150+500 $
$\Rightarrow 25 D B=650 $
$\Rightarrow D B=\dfrac{130}{5} $
$\Rightarrow D B=26 \mathrm{~cm}$
3. In given figure, $A B=10 \mathrm{~cm}, D C=15 \mathrm{~cm}, B C=35 \mathrm{~cm}, A D=40 \mathrm{~cm}$ and $D B=25 \mathrm{~cm}$, then find $A C$.
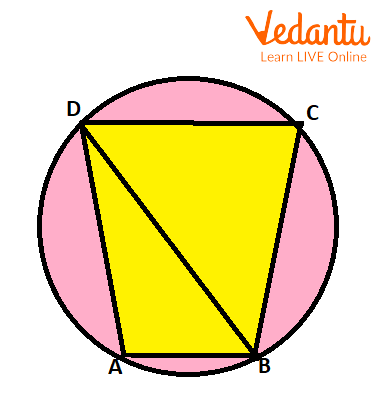
To Find the Diagonal of Cyclic Quadrilateral
Ans: By Ptolemy's Theorem, we have,
$D B \times A C=A B \times D C+A D \times B C$
Putting values, we get,
$\Rightarrow A C \times 25=10 \times 15+40 \times 35 $
$\Rightarrow 25 A C=150+1400 $
$\Rightarrow 25 A C=1550 $
$\Rightarrow A C=\dfrac{310}{5} $
$\Rightarrow A C=62 \mathrm{~cm}$
Conclusion
We have discussed the detailed proof of Ptolemy Theorem and its applications in this article. Ptolemy Theorem forms a fundamental tool for cyclic quadrilaterals. In all, we can say that Ptolemy's Theorem is a fantastic theorem which helps us in solving problems of cyclic quadrilaterals easily.
Important Formulas to Remember
For a cyclic quadrilateral ABCD, with AC and BD be the diagonals we have, $\left| {AC} \right|.\left| {BD} \right| = \left| {AB} \right|.\left| {CD} \right| + \left| {BC} \right|.\left| {DA} \right|$.
Important Points to Remember
A quadrilateral is said to be cyclic if all the vertices of the quadrilateral lie on the circumference of the circle.
List of Related Articles
FAQs on Ptolemy Theorem for Cyclic Quadrilaterals
1. Is there any relation for other types of quadrilaterals also?
Yes, Ptolemy Theorem also gives us a generalised relation apart from the equality stated in the article. The generalisation is in the form of inequality and the inequality is often referred to as Ptolemy's Inequality. For the inequality to hold true, points A, B, C, D are not necessarily cyclic points, i.e., the points may or may not lie on a circle.
$|A C| \cdot|B D|>|A B| \cdot|C D|+|B C| \cdot|D A|$.
The above inequality holds for every type of quadrilateral, not necessarily cyclic quadrilateral.
2. What is Carnot's Theorem?
Carnot's Theorem states that for a triangle ABC with circumcentre O, circumradius R and in inradius r, the algebraic sum of the distances (taken with appropriate sign) of sides, i.e., A, B, C, respectively, from the circumcentre O is equal to R+r, i.e., the sum of circumradius and inradius of triangle ABC. Carnot's Theorem is based on Ptolemy's Theorem and proof of Carnot's Theorem is derived using Ptolemy's Theorem. Carnot's Theorem is applicable in the case of all three types of triangles, i.e., acute angle triangle, obtuse angle triangle, and right-angle triangle.
3. State converse of Ptolemy Theorem.
Ptolemy's theorem states that in a cyclic quadrilateral, the product of diagonals of the quadrilateral is equal to the sum of products of the lengths of opposite sides of the quadrilateral. So, the converse of the Ptolemy Theorem is given as: If in a quadrilateral, the sum of the products of its two pairs of opposite sides quadrilateral is equal to the product of the diagonals of the quadrilateral, then the quadrilateral can be inscribed in a circle, i.e., the quadrilateral is cyclic.
