Rational Numbers

A rational number is defined as a fraction of two numbers in the form of \[\dfrac{p}{q}\] where p and q can be any integer but q is not equal to 0. Algebra is the branch of mathematics that deals with symbols and variables. Rational numbers consist of all types of numbers including Natural numbers, Whole numbers, also 0, etc. Integers consist of both positive and negative numbers. So we can classify Rational numbers as Positive and negative rational numbers. For example, positive rational numbers are

\[\dfrac{1}{5},\dfrac{2}{4},\dfrac{{17}}{{90}}\], etc.

Negative rational numbers are as follows

\[\dfrac{-2}{4},\dfrac{-10}{5},\dfrac{{-90}}{{34}}\] etc.

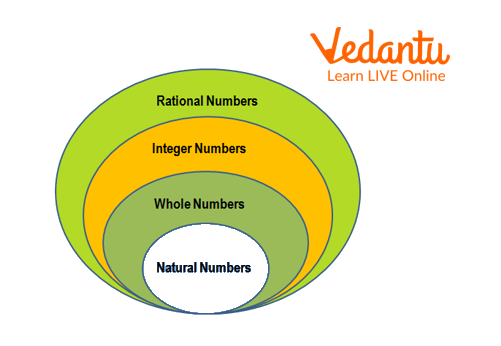
Number Chart

Positive and Negative Rational Numbers

The rational numbers can be +ve and -ve. Positive rational numbers are referred to as those rational numbers whose numerators and denominators both are either positive or negative. Positive rational numbers are always greater than 0. For example, \[\dfrac{8}{9}\]after dividing, we get 0.88 which is greater than 0, so \[\dfrac{8}{9}\] is a positive rational number.

Negative rational numbers are referred to as those rational numbers whose numerators and denominators have different signs making them negative. Negative rational numbers are always less than 0. For example, \[\dfrac{-12}{13}\]gives - 0.92 which is a negative rational number and also is smaller than 0.

What is a Positive Number?

Positive numbers can also be illustrated by the number line. The numbers which are on the right side of the number line are considered positive numbers as shown in the image given below.

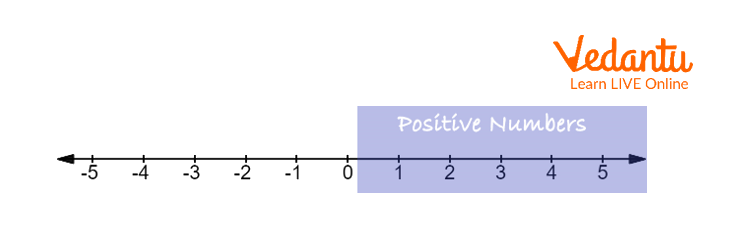
Number Line

Positive numbers are numbers whose value is always greater than 0. When a number does not contain any sign, it is assumed to be a positive number. For example, 45 and +45 both are the same and also positive numbers.

The Rational Number that is Equal to its Negative

Zero is the only rational number that is equal to its negative rational number because zero is neither considered positive nor negative, in other words, zero is a signless number.

For more illustration, let us take an example, here zero has no value if it is positive it is considered zero, and if negative also it is considered zero. From the above statement, we concluded that if zero is positive or negative, it is always zero, therefore 0 = 0.

Can Denominators be Negative?

Yes, the denominators can be negative in a rational number because as we know about the negative rational number discussed above in the article, it states that either numerators or denominators of a rational number can be negative, so by this statement, we can conclude that the denominator of a rational number is negative.

For example, let's consider a rational number that is negative \[\dfrac{-1}{2}\]; in this rational number, any of the numerators or denominators can be negative.

Another example \[\dfrac{1}{-2}\], multiplying both the denominator and numerator by -1 we get \[\dfrac{-1}{2}\]. So we can conclude that denominators can also be negative in a rational number.

Identify the Positive and Negative Rational Numbers

Rational numbers are classified into three parts positive, 0, and negative rational numbers.

If both the numerator and denominator of a rational number have similar signs like both are positive or both are negative, then it is a positive rational number and when the numerator is negative and the denominator is positive or vice versa, then it is a negative rational number.

For example, \[\dfrac{1}{5}\]and \[\dfrac{-3}{-2}\] both are positive rational numbers. And \[\dfrac{-17}{9},\dfrac{45}{-7}\] both are negative rational numbers.

Can Rational Numbers be Negative?

Yes, rational numbers can be negative. We have already discussed in the article above that negative rational numbers are referred to as those rational numbers whose numerators and denominators have different signs making them negative. Negative rational numbers are always less than 0. So we can conclude that rational numbers can also be negative.

Rational Number - Addition and Subtraction

In the same manner that fractions may be added and subtracted, rational numbers can be added and subtracted. To add or subtract two rational numbers, first, equalize their denominators, then add their numerators.

Example : 

\[\dfrac{1}{2}\]\[-\]\[(-\dfrac{2}{3})\]

=\[\dfrac{1}{2}\]+\[\dfrac{2}{3}\]

L.C.M of 2,3=6

=\[\dfrac{1}{2}\times\dfrac{3}{3}\]+\[\dfrac{2}{3}\times \dfrac{2}{2}\]

=\[\dfrac{3}{6}\]+\[\dfrac{4}{6}\]

=\[\dfrac{7}{6}\]

=\[1\dfrac{1}{6}\]

Rational Number - Multiplication and Division

Rational numbers can be multiplied and divided in the same way as fractions. We multiply the numerators and denominators of any two rational integers independently before simplifying the resultant fraction.

Example: 

=\[\dfrac{3}{5} \times \dfrac{-2}{7}\]

=$\dfrac{3\times{-2} }{5\times7}$

=$\dfrac{-6}{35}$

To divide any two fractions, multiply the first fraction (dividend) by the reciprocal of the second fraction (which is the divisor).

Example: 

$\dfrac{\dfrac{3}{5}}{\dfrac{2}{7}}$

=$\dfrac{3}{5}\times\dfrac{7}{2}$

=$\dfrac{21}{10}$

Interesting Facts

• All fractions can be rational numbers but all rational numbers cannot be a fraction.

• Rational numbers are only created for inadequate measurements and are created by the Greek mathematician Pythagoras.

• Rational is uncountable or you can say that these are infinite.

• Every rational number is called a real number.

Solved Problems

1. How \[\dfrac{-3}{-7}\] is a positive rational number?

Ans: To determine it, we have to multiply the numerator and denominator by -1 \[\dfrac{-3\times -1}{-7\times -1}\], we get \[\dfrac{3}{7}\] which is a positive rational number.

2. Is 31 considered a positive rational number?

Ans: 31 can be expressed in the form of a ratio \[\dfrac{31}{1}\] in which both the numerator and denominator, i.e., 31 and 1 are positive integers.

Therefore, 31 is considered a positive rational number.

3. Bhudu spends \[\dfrac{1}{4}\] of his monthly earnings on rent, \[\dfrac{3}{5}\] on food, and \[\dfrac{1}{10}\] on monthly usuals. What fractional part of his earnings is left with him for other expenses?

Ans: Amount spent for rent = \[\dfrac{1}{4}\]

Amount spent for food = \[\dfrac{3}{5}\]

Amount spent for monthly usual = \[\dfrac{1}{10}\]

Required amount left over = 1 - [ \[\dfrac{1}{4}\] + \[\dfrac{3}{5}\] + \[\dfrac{1}{10}\]]

L.C.M (4, 5, 10) = 20

= 1 - [ \[\dfrac{5+12+2}{20}\]]

= 1 - \[\dfrac{19}{20}\]

= \[\dfrac{20-19}{20}\]

= \[\dfrac{1}{20}\]

Key Features

• A rational number is the ratio of two integers, where the denominator of that ratio should not be zero.

• Rational numbers are of three types positive rational numbers, negative rational numbers, and 0.

• Natural numbers, whole numbers, integers, and fractions with integers are rational numbers.

Practice Questions

1. Determine if 7 is a positive rational number.

Ans: 7 is a positive rational number.

2. List any five positive rational numbers.

Ans: 87, 64, 98, 5968, 323.

3. Find the five rational numbers between 7 and 8.

Ans:\[\dfrac{1}{3},\dfrac{2}{4},\dfrac{9}{3},\dfrac{4}{2},\dfrac{3}{1}\]