Right Circular Cylinder

In this article, we'll learn all about cylinders, which are among the most common three-dimensional shapes we encounter in our daily lives. A cylinder is quite a popular geometrical shape. It is the foundation of many interesting everyday products, such as a can, gas cylinders, rollers, tube lights, chalk, pipe, batteries, cylindrical tumblers/flask, drums, and so on. These solids have circular shape bases that are congruent and parallel. Can you find any cylindrical shapes in your surroundings?

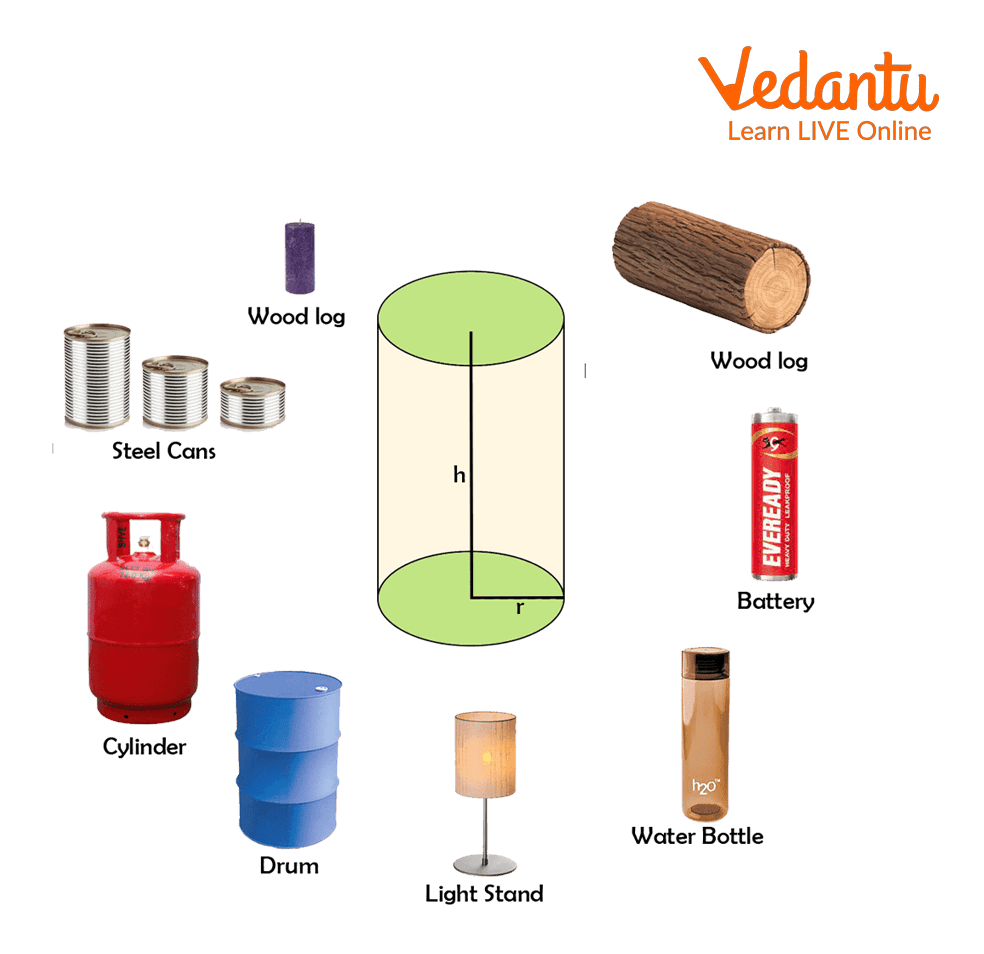
Cylindrical Shapes

What is the Right-Circular Cylinder?

A right-circular cylinder can be defined as a three-dimensional solid geometrical figure of two parallel circular shapes joined by a curved surface. The ends of the right circular cylinder are closed circles and are congruent and parallel to one another. The right cylinder is another name for a right circular cylinder.

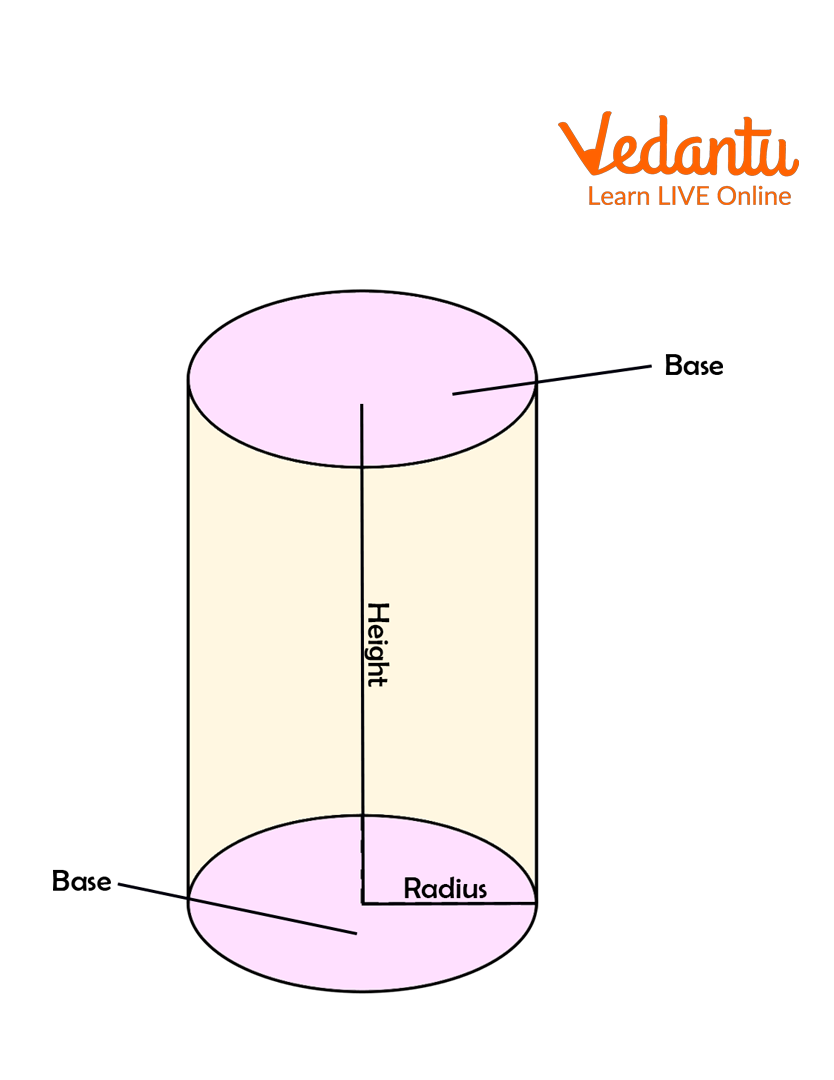
Cylinder

Parts of Cylinder

1. Base: It refers to each of a right circular cylinder's circular ends.

2. Axis: It refers to the line segment that connects the centres of two circular bases and is perpendicular to the base of the right circular cylinder.

3. Radius (r): It refers to the circular base's radius.

4. Height (h): It refers to the length of the cylinder's axis.

Properties of the Right-Circular Cylinder

Some properties of the right-circular cylinder are:

1. There are two edges present in a right circular cylinder.

2. The right cylinders have no corners so zero vertices are present.

3. Cylindrical bases are always parallel to one another.

4. The shape we obtain is a circle if a plane cuts the right cylinder horizontally and parallel to the bases.

5. A right cylinder is created when a rectangle is rotated around one side as the axis of revolution.

6. Longest diagonal of a cylinder is given by $d^2 = 4 \times r^2 + h^2$

Lateral or Curved Surface Area of the Right-Circular Cylinder

The total area that the figure's curving surfaces cover is known as the CSA. It has a square unit of measurement. The lateral surface of the right circular cylinder is the curved surface that links the two circular shape bases, and its area is given by:

$LSA=(Perimeter\:of\:the\:circular\:ends)\times height(h)$

$\:\:\:=2\pi rh\:sq\:unit$

Total Surface Area of the Right-Circular Cylinder

The total surface area of the right circular cylinder is equal to the sum of the bases of both circles plus the CSA.

$TSA=Lateral\:Surface\:Area+2\times(Area\:of\:the\:circle)$

$\:\:\:=2\pi rh+2\pi r^2$

$\:\:\:=2\pi r(h+r) sq\:unit$

Volume of the Right-Circular Cylinder

The volume of any 3-D solid is the amount of space it can hold. It is measured in cubic units like $cm^3$, $m^3$, etc. Thus, the right-circular cylinder formula for volume is given by: $ Volume=\pi r^2 h$ cubic unit

Solved Examples of Cylinders

Example 1: Find the volume of the right cylinder whose height is 20 cm and radius is 5 cm. Take $\pi$=3.14.

Solution: Given h=20 cm and r=5cm

We know that the volume of the right-circular cylinder is given by:

$Volume =\pi r^2 \mathrm{h}$

$\:\:\:\:\:=3.14\times(5)^2\times20$

$\:\:\:\:\:=1570\:cm^3$

Example 2: The radius and height of a right circular cylinder are given as 2.4 m and 6 m, respectively. Find the lateral and total surface area of the right cylinder. Take $\pi$ = 3.14.

Solution: Given r=2.4 m and h=6m

We know that the lateral or curved surface area of the right-circular cylinder is given by:

$LSA =2\pi \mathrm{r}\mathrm{h}$

$\:\:\:=2\times3.14\times2.4\times6$

$\:\:\:=90.432\:m^2$

Now, for the total surface area;

$T S A =2 \pi r(\mathrm{h}+\mathrm{r}) $

$\:\:\:=2 \times 3.14 \times 2.4(6+2.4)$

$\:\:\:=2 \times 3.14 \times 20.16$

$\:\:\:=126.6048 \mathrm{~m}^2$

Practice on Your Own

Q1. Find the total surface area and volume of the right-circular cylinder whose radius and height are 5 cm and 14.9, respectively. Take $\pi=3.14$.

Q2. Find the radius of the cylinder whose lateral surface area is 5024 $m^2$ and height is 8 m. Take $\pi=3.14$.

Ans1: TSA=624.86 $cm^2$; Volume=1169.65 $cm^3$.

Ans2: 100 m.

Quick Summary

Below is a quick summary on the topic right circular cylinder. For more details, you can access the free resources available on the Vedantu website for the state board, CBSE, ICSE, and competitive examinations.

Conclusion

In this article, we have discussed that a cylinder is a 3-D geometric figure having two parallel circular shapes joined by a curved surface. When the axis is perpendicular to the radius, the cylinder is referred to as a right circular cylinder. The real-life cylinder examples provided in this article will assist you in quickly recognizing the cylindrical shapes that surround us.