Round Off - A Fun Learning

Rounding is the process of replacing a number with an approximation that has a shorter, simpler, or more accurate description. For instance, changing 23.4476 to 23.45, 312/937 to 1/3, or 2 to 1.414. Rounding is frequently done to get a value that is simpler to report and explain than the original. For example, a quantity that was computed as 123,456 but is known to be accurate to within a few hundred units is usually better stated as "about 123,500." On the other hand, rounding exact numbers will result in a small amount of round-off error being reported. When reporting many computations, rounding is essentially unavoidable, especially when dividing two numbers in integer or fixed-point arithmetic, computing mathematical functions like sines, square roots, and logarithms, or using a floating-point representation with a fixed number of significant digits. In a series of calculations, these rounding errors typically add up and, in some unfortunate circumstances, they might represent the outcome meaninglessly.

Rules of Rounding Numbers

Round Off

When a number is rounded off, its value is maintained but is moved closer to the following number, simplifying the number. It is done for whole numbers as well as decimals at different places such as hundreds, tens, tenths, etc. To maintain the significant figures, numbers are rounded off. Simply put, the number of figures that are known with some degree of reliability is the number of significant figures in a result.

According to legend, the number 13.2 contains three significant figures. Digits greater than zero are always important. There are six significant digits in the number 3.14159. (all the numbers give you useful information). As a result, 67 has two significant digits, while 67.3 has three.

How to Round off Decimal Numbers?

Rounding rules for decimal numbers are as follows:

• Determine the rounding digit and look at its right-hand side.

• If the digits on the right-hand side are less than 5, consider them equal to zero.

• If the digits on the right-hand side are greater than or equal to 5, then add +1 to that digit and consider all other digits as zero.

Decimal Round off 

How to Round off Whole Numbers?

Rounding rules for whole numbers are as follows:

• To get an accurate final result, always choose the smaller place value.

• Look for the next smaller place which is towards the right of the number that is being rounded off. For example, if you are rounding off a digit from a tens place, look for a digit in one place.

• If the digit in the smallest place is less than 5, then the digit is left untouched. Any number of digits after that number becomes zero and this is known as rounding down.

• If the digit in the smallest place is greater than or equal to 5, then the digit is added with +1. Any digits after that number become zero and this is known as rounding up.

Whole Number Round Off

Rounding off to the Nearest Ten

• A good way of explaining this is to use a number line.

• If the unit of the number is less than five, the number needs to be rounded down.

• If the unit of the number is 5 or above, the number needs to be rounded up.

• So 32 would be rounded down to 30, 35 would be rounded up to 40 and 38 would also be rounded up to 40:

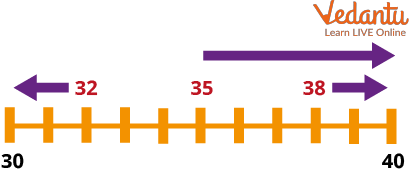
Number Line

Rounding off to the Nearest Hundred

• If the tens digit is less than 50 the number is rounded down.

• If the tens digit is 50 or more, the number is rounded up. (The unit digit can be ignored when rounding a three-digit number to the nearest 100.)

• So 834 would be rounded down to 800, 851 would be rounded up to 900 and 876 would be rounded up to 900:

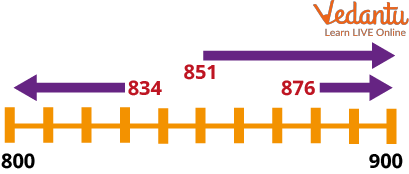
Number Line From 800 to 900

Summary

Round-off errors of a tiny amount will be reported when accurate figures are rounded. Rounding is essentially inevitable when summarising a large number of calculations, particularly when dividing two numbers in fixed-point or integer arithmetic, computing mathematical functions like sines, square roots, and logarithms, or using a floating-point representation with a fixed number of significant digits. These rounding errors usually mount up in a succession of calculations and, in some terrible cases, they could render the result meaningless.